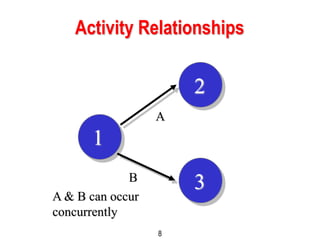
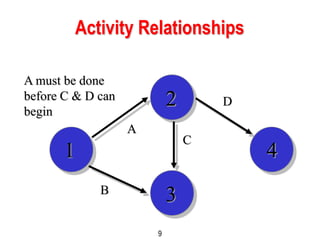
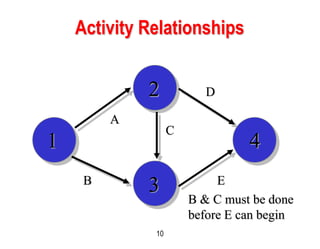
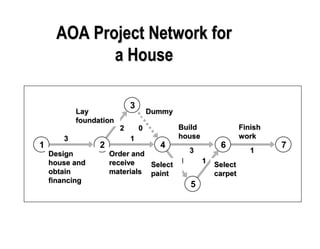
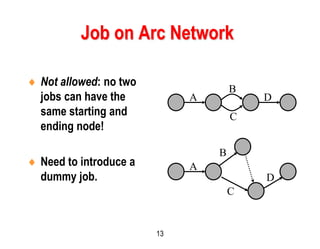
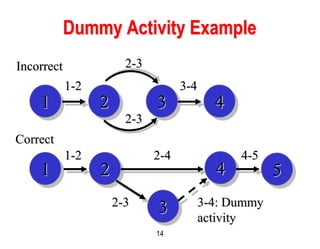
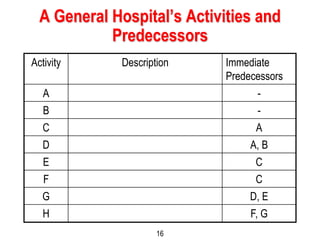
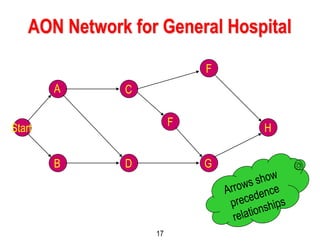
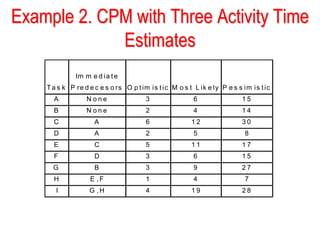
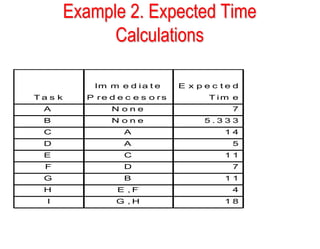
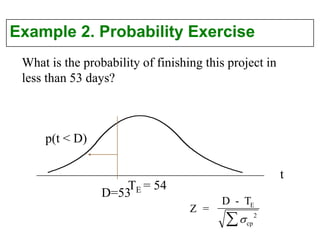
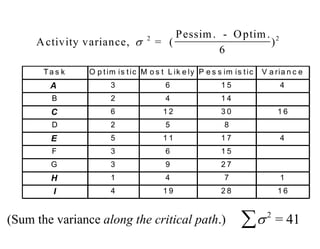
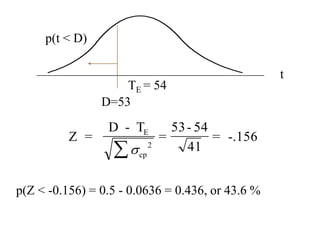
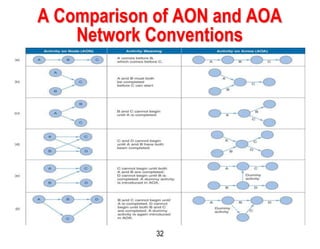
This document discusses project scheduling techniques CPM and PERT. It provides background on their development in the 1950s and describes their key features. Both techniques use network diagrams to show task relationships and interdependencies. They help determine if a project is on schedule or budget, and identify critical paths and resources. The document outlines the common six steps to CPM and PERT and provides examples of network diagrams and calculations.

1. 1
Project Scheduling
CPM/PERT

2. 2
 Network techniques
 Developed in 1950’s
 CPM by DuPont for chemical plants (1957)
 PERT by Booz, Allen & Hamilton with the U.S.
Navy, for Polaris missile (1958)
 Consider precedence relationships and
interdependencies
 Each uses a different estimate of activity times
PERT and CPM

3. why networks/CPM/PERT?
 Gantt charts don’t explicitly show
task relationships
 don’t show impact of delays or
shifting resources well
 network models clearly show
interdependencies

4. 4
Is the project on schedule, ahead of schedule,
or behind schedule?
Is the project over or under cost budget?
Are there enough resources available to finish
the project on time?
If the project must be finished in less than the
scheduled amount of time, what is the way to
accomplish this at least cost?
Questions Which May Be
Addressed by PERT & CPM

5. 5
The Six Steps Common to PERT & CPM
 Define the project and prepare the work breakdown
structure,
 Develop relationships among the activities. (Decide
which activities must precede and which must follow
others.)
 Draw the network connecting all of the activities
 Assign time and/or cost estimates to each activity
 Compute the longest time path through the network.
This is called the critical path
 Use the network to help plan, schedule, monitor, and
control the project

6. 6
Terminology
 Activity: A specific or set of tasks required by
the project
 Event: Outcome of one or more activities
 Network: Combination of all activities and
events
 Path: Series of connected activities or
between any two events
 Critical path: Longest - Any delay would delay
the project
 Slack/float: Allowable slippage for a path

7. 7
Activity Relationships
Predecessor – an activity that is required to
start or finish before the next activity(s) can
proceed
Successor – an activity that must start or
finish after the previous activity can finish
Types of relationships are defined from the
predecessor to the successor

8. 8
1
A
B
A & B can occur
concurrently
2
3
Activity Relationships

9. 9
1 4
2
3
A
B
C
A must be done
before C & D can
begin
D
Activity Relationships

10. 10
1 4
2
3
A
B E
C
B & C must be done
before E can begin
D
Activity Relationships

11. AOA Project Network for
a House
3
2 0
1
3
1 1
1
1 2 4 6 7
3
5
Lay
foundation
Design
house and
obtain
financing
Order and
receive
materials
Dummy
Finish
work
Select
carpet
Select
paint
Build
house

12. 12
 Activities are defined often by beginning &
ending events
 Every activity must have unique pair of
beginning & ending events
 Otherwise, computer programs get confused
 Dummy activities maintain precedence
 Consume no time or resources
Dummy Activities

13. 13
Job on Arc Network
 Not allowed: no two
jobs can have the
same starting and
ending node!
 Need to introduce a
dummy job.
A
B
D
C
A
B
D
C

14. 14
1 4
3
1-2
2-3
Incorrect
1 4
2
3
5
2
2-3
3-4
1-2
2-3
2-4 4-5
3-4: Dummy
activity
Correct
Dummy Activity Example

15. 15
Critical Path
The longest continuous path of activities
through a project, which determines the
project end date

16. 16
A General Hospital’s Activities and
Predecessors
Activity Description Immediate
Predecessors
A -
B -
C A
D A, B
E C
F C
G D, E
H F, G

17. 17
AON Network for General Hospital
Start
A
B
C
D
F
F
G
H

18. Program Evaluation and
Review Technique (PERT)
PERT is based on the assumption that an
activity’s duration follows a probability
distribution instead of being a single value.
The probabilistic information about the
activities is translated into probabilistic
information about the project.

19. PERT
 reflects PROBABILISTIC nature of durations
 assumes BETA distribution
 same as CPM except THREE duration
estimates
optimistic
most likely
pessimistic

20. PERT Calculation
a = optimistic duration estimate
m = most likely duration estimate
b = pessimistic duration estimate
expected duration:
variance:
Te
a + 4m + b
6
V =
b - a
6







2

21. 21
 3 time estimates
 Optimistic times (a)
 Most-likely time (m)
 Pessimistic time (b)
 Follow beta distribution
 Expected time: t = (a + 4m + b)/6
 Variance of times: v = (b - a)2/6
PERT Activity Times

22. 22
Variability of Completion Time for
Noncritical Paths
Variability of times for activities on non-critical
paths must be considered when finding the
probability of finishing in a specified time.
Variation in non-critical activity may cause
change in critical path.

23. 23
Advantages of PERT/CPM
 Especially useful when scheduling and controlling
large projects.
 Straightforward concept and not mathematically
complex.
 Graphical networks aid perception of relationships
among project activities.
 Critical path & slack time analyses help pinpoint
activities that need to be closely watched.
 Project documentation and graphics point out who is
responsible for various activities.
 Applicable to a wide variety of projects.
 Useful in monitoring schedules and costs.

24. 24
Questions Answered by CPM & PERT
Completion date?
On Schedule?
Within Budget?
Critical Activities?
How can the project be finished early at the
least cost?

25. 25
 Assumes clearly defined, independent, &
stable activities
 Specified precedence relationships
 Activity times (PERT) follow beta distribution
 Subjective time estimates
 Over-emphasis on critical path
Limitations of PERT/CPM

26. Example 2. CPM with Three Activity Time
Estimates
Ta s k
Im m e d ia t e
P re d e c e s o rs O p t im is t ic M o s t L ik e ly P e s s im is t ic
A N o n e 3 6 1 5
B N o n e 2 4 1 4
C A 6 1 2 3 0
D A 2 5 8
E C 5 1 1 1 7
F D 3 6 1 5
G B 3 9 2 7
H E , F 1 4 7
I G , H 4 1 9 2 8

27. Example 2. Expected Time
Calculations
T a s k
Im m e d i a t e
P re d e c e s o rs
E x p e c t e d
T i m e
A N o n e 7
B N o n e 5 . 3 3 3
C A 1 4
D A 5
E C 1 1
F D 7
G B 1 1
H E , F 4
I G , H 1 8

28. Example 2. Probability Exercise
What is the probability of finishing this project in
less than 53 days?
p(t < D)
TE = 54
Z =
D - TE
cp
2


t
D=53

29. Activity variance, = (
Pessim. - Optim.
6
)
2 2

Ta s k O p tim is tic M o s t L ik e ly P e s s im is tic V a ria n c e
A 3 6 1 5 4
B 2 4 1 4
C 6 1 2 3 0 1 6
D 2 5 8
E 5 1 1 1 7 4
F 3 6 1 5
G 3 9 2 7
H 1 4 7 1
I 4 1 9 2 8 1 6
(Sum the variance along the critical path.) 2
 = 41

30. p(Z < -0.156) = 0.5 - 0.0636 = 0.436, or 43.6 %
Z =
D - T
=
53- 54
41
= -.156
E
cp
2


TE = 54
p(t < D)
t
D=53

31. 32
A Comparison of AON and AOA
Network Conventions