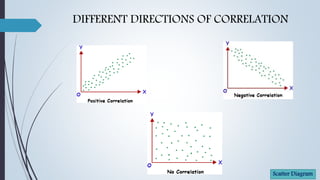
The document discusses correlation, defining it as a statistical technique for measuring the relationship between variables, specifically focusing on covariance and types of correlation. It outlines methods of studying correlation, interpretation of correlation coefficients, and highlights advantages and disadvantages of correlational studies. Additionally, it provides examples of real-life correlations and calculates the correlation coefficient and coefficient of determination in relation to IQ scores and GPA.

2. CORRELATION
Statistical techniques for measuring the closeness of the
relationship between variables.
It measures the degree to which changes in one variable are
associated with changes in another.
It can only indicate the degree of association or covariance
between variables. Covariance is a measure of the extent to which
two variables are related.

3. TYPES OF CORRELATION
The important ways of classifying the correlation are:
1. Positive and Negative
2. Simple , Partial and Multiple
3. Linear and non-Linear.
METHODS OF STUDYING CORRELATION
The following are the important methods of ascertaining between two
variables.
 Scatter diagram method
Scatter Diagram Method-The simplest device for studying correlation
between two variables is a special type of dot chart.

4. CORRELATION - INTERPRETATION
Positive r indicates positive linear association between x and y or
variables, and negative r indicates negative linear relationship
R –s always between -1 and +1
The strength increases as r moves away from zero toward wither -
1 or +1
The extreme values +1 and -1 indicate perfect linear relationship

5. DIFFERENT DIRECTIONS OF CORRELATION
Scatter Diagram

6. COMPUTING THE CORRELATION COEFFICIENT
separatelyvaryYandXwhichtodegree
thervary togeYandXwhichtodegree
r
]
)(
[]
)(
[
))((
2
2
2
2
NN
N
ss
COV
yx
xy







The ratio of the joint variation of X and Y (covariance) relative to the variation of X and Y
considered separately

7.  The relationship between IQ scores and grade point
average? (N=12 students)
IQ and Grade Point Average
Student No X Y X2
Y2
XY
1 110 1.0 12,100 1.00 110.0
2 112 1.6 12,544 2.56 179.2
3 118 1.2 13,924 1.44 141.6
4 119 2.1 14,161 4.41 249.9
5 122 2.6 14,884 6.76 317.2
6 125 1.8 15,625 3.24 225.0
7 127 2.6 16,129 6.76 330.2
8 130 2.0 16,900 4.00 260.0
9 132 3.2 17,424 10.24 422.4
10 134 2.6 17,956 6.76 348.4
11 136 3.0 18,496 9.00 408.0
12 138 3.6 19,044 12.96 496.8
Total 1503 27.3 189,187 69.13 3488.7
The correlation coefficient is independent of change of origin and scale.
Interval or ratio level data are required for correlation analysis.

8. 86.0856.0
088.81
375.69
]
12
)3.27(
13.69[]
12
)1503(
187,189[
12
)3.27(1503
7.3488
]
)(
[]
)(
[
))((
22
2
2
2
2











NN
Nr
COMMENT= The Correlation Is Here 0.86 For Among Student.

9. Strong Positive Correlation relationship

10. THE COEFFICIENT OF DETERMINATION
It is the primary way we can measure the extent or strength of the
association that exists between two variables x & y . because we have
used a sample of points to develop regression lines .
it is denoted by = 2
r
2
r = 0.862
= 0.7396
Comment: 73%𝑜𝑓 𝑡𝑜𝑡𝑎𝑙 𝑣𝑎𝑟𝑖𝑎𝑡𝑖𝑜𝑛 𝑖𝑠 𝑒𝑥𝑝𝑙𝑎𝑖𝑛𝑒𝑑 𝑏𝑦 𝑡ℎ𝑒 𝑑𝑒𝑝𝑒𝑛𝑑𝑒𝑛𝑡 𝑡𝑜 𝑖𝑛𝑑𝑒𝑝𝑒𝑛𝑑𝑒𝑛𝑡 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒.
73% relation between the iQ score and grade point,

11. ADVANTAGES OF CORRELATIONAL STUDIES
 Show the amount (strength) of relationship present
 Can be used to make predictions about the variables studied
 Often easier to collect correlational data, and interpretation is fairly straightforward.
DISADVANTAGES OF CORRELATIONAL STUDIES
 Can’t assume that a cause-effect relationship exists
 Little or no control (experimental manipulation) of the variables is possible
 Relationships may be accidental or due to a third, unmeasured factor common to the 2
variables that are measured
 Spurious correlations and Mediators

12. REAL LIFE EXAMPLES OF CORRELATIONS
Positive correlation between test average and study time
Positive correlation between calories burned and treadmill
running time
Negative correlation between age of tadpole and length of tail
Negative correlation between average temperature and cost
sale.