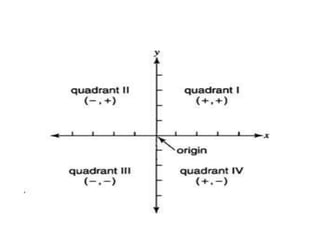
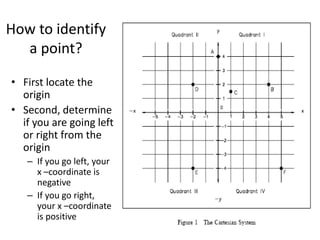
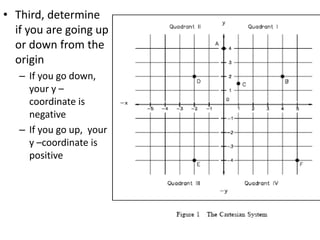
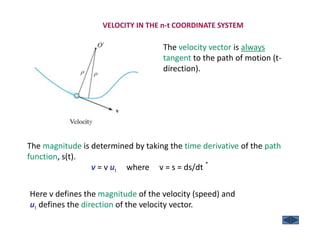
The document describes the Cartesian coordinate system and the normal-tangential coordinate system. The Cartesian system uses perpendicular x and y axes to locate points in a plane using ordered pairs (x,y). The normal-tangential system is used to describe motion along a curved path, with the t-axis tangent to the path and the n-axis perpendicular, pointing toward the center of curvature. In this system, a particle's position is defined by its distance s along the curve, and its velocity is always in the t-direction while its acceleration has components in both the t and n directions.

1. Cartesian
Coordinate
System
Called also
rectangular
coordinate
system

3. Definitions
• X-axis – the horizontal axis
• Y –axis – the vertical axis
• Rectangular coordinate system: where the x-axis
and the y-axis intersect
• Ordered pair: identifies the location of a point on
the rectangular coordinate system
• (x coordinate, y coordinate)
• Origin: (0,0) – intersection of the x and y axis
• Quadrant: a section of the rectangular
coordinate system

5. How to identify
a point?
• First locate the
origin
• Second, determine
if you are going left
or right from the
origin
– If you go left, your
x –coordinate is
negative
– If you go right,
your x –coordinate
is positive

6. • Third, determine
if you are going up
or down from the
origin
– If you go down,
your y –
coordinate is
negative
– If you go up, your
y –coordinate is
positive

7. How to identify the quadrant?
• First – locate where
your point is
• Second – check your
graph on which
quadrant it is in.

8. When a particle moves along a curved path, it is sometimes convenient
to describe its motion using coordinates other than Cartesian. When the
path of motion is known, normal (n) and tangential (t) coordinates are
often used.
In the n-t coordinate system, the
origin is located on the particle
(thus the origin and coordinate
system move with the particle).
The t-axis is tangent to the path (curve) at the instant considered,
positive in the direction of the particle’s motion.
The n-axis is perpendicular to the t-axis with the positive direction
toward the center of curvature of the curve.
NORMAL AND TANGENTIAL COMPONENTS
(Section 12.7)

9. The position of the particle at any
instant is defined by the distance, s, along the curve from a
fixed reference point.
The positive n and t directions are
defined by the unit vectors un and ut,
respectively.
The center of curvature, O’, always
lies on the concave side of the curve.
The radius of curvature, r, is defined
as the perpendicular distance from
the curve to the center of curvature at
that point.
NORMALAND TANGENTIAL COMPONENTS (continued)

10. VELOCITY IN THE n-t COORDINATE SYSTEM
The velocity vector is always
tangent to the path of motion (t-
direction).
The magnitude is determined by taking the time derivative of the path
function, s(t).
v = v ut where v = s = ds/dt
.
Here v defines the magnitude of the velocity (speed) and
ut defines the direction of the velocity vector.

11. ACCELERATION IN THE n-t COORDINATE SYSTEMS
Acceleration is the time rate of change of velocity:
a = dv/dt = d(vut)/dt = vut + vut
.
Here v represents the change in the
magnitude of velocity and ut represents
the rate of change in the direction of ut.
.
.
.
.
.