This presentation explores the fascinating relationship between linear and angular motion in the context of human movement, bridging concepts from physics and biomechanics to deepen our understanding of how the body moves through space. Whether you're a student, educator, athlete, or health professional, this slide deck offers a clear and practical explanation of how linear quantities (like displacement, velocity, and acceleration) relate to angular quantities (such as angular displacement, angular velocity, and angular acceleration) in everyday physical activities. 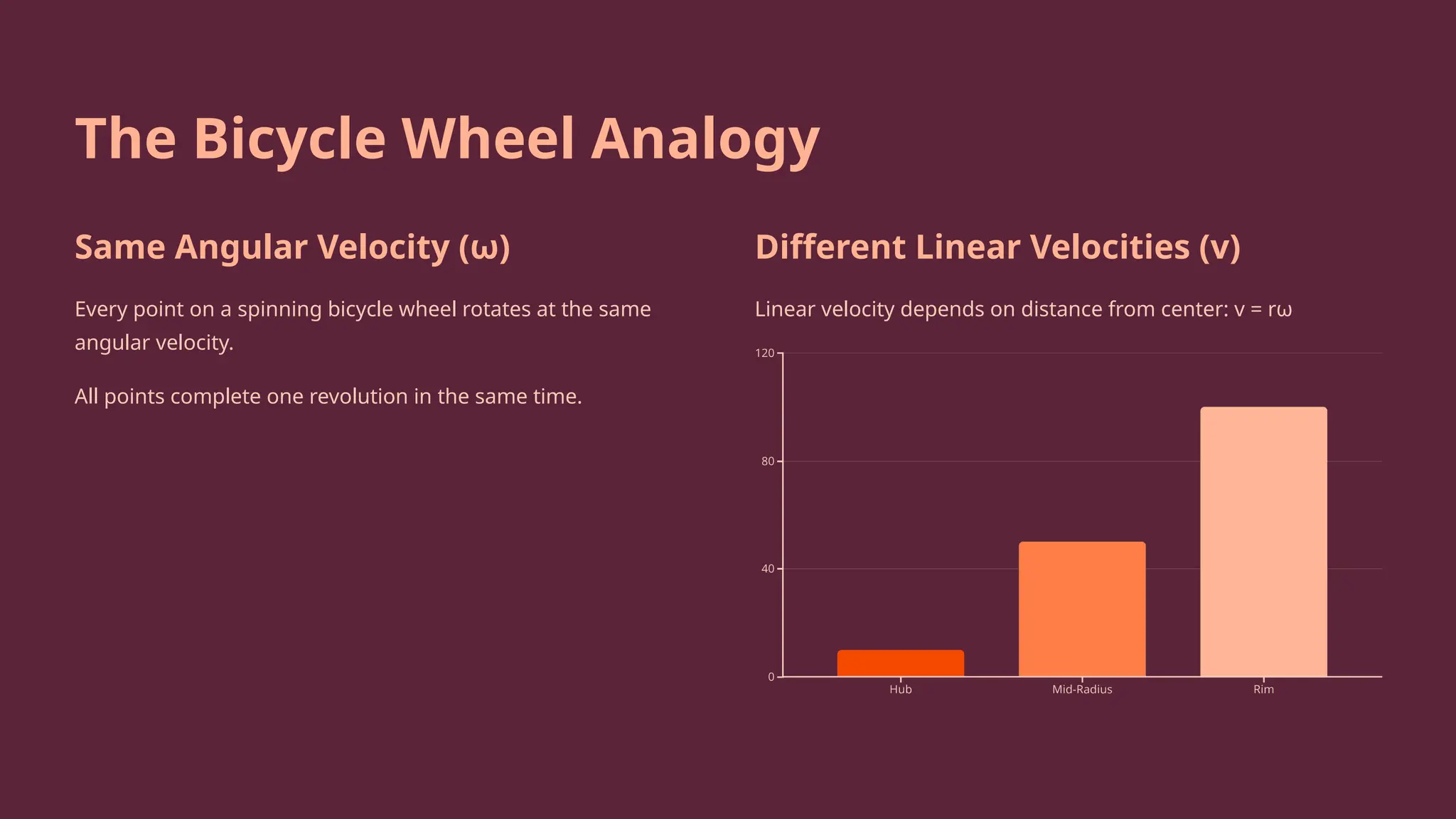Key highlights include: Fundamental definitions of linear and angular motion Real-life examples of human movement, such as walking, running, throwing, and jumping Mathematical relationships between linear and angular quantities (e.g., v = r ω v=rω, a = r α a=rα) Applications in sports science, physical therapy, and ergonomics Visual diagrams and motion analysis to illustrate concepts clearly Interactive questions and reflections to encourage deeper learning By connecting these two types of motion, we gain insights into how joints rotate, how limbs translate through space, and how forces are distributed during movement. This knowledge is essential for improving performance, preventing injury, and designing effective training or rehabilitation programs. Perfect for use in physics classes, PE and sports science modules, or biomechanics workshops, this presentation simplifies complex concepts and shows how physics is deeply embedded in the way we move.

1. Connecting Linear and
Angular Quantities in
Human Movement
Human movement naturally connects linear and angular motion in
fascinating ways. Through simple activities like exercise, dance, and
gymnastics, we can see physics in action.
by ANGELIQUE TOLENTINO DEL ROSARIO

2. What Are Linear
Quantities?
Linear Displacement
The distance moved in a straight line, measured in meters (m)
Linear Velocity
How fast an object moves in a straight line, measured in meters per
second (m/s)
Linear Acceleration
How quickly velocity changes, measured in meters per second squared
(m/s²)

3. What Are Angular Quantities?
Angular Displacement (θ)
The angle through which an object
rotates, measured in radians
Angular Velocity (ω)
How quickly an object rotates,
measured in radians per second (rad/s)
Angular Acceleration (α)
Rate of change of angular velocity, in
radians per second squared (rad/s²)

4. How Are They Related?
Where r is the radius from the pivot point or axis of rotation.
These equations connect:
• Arc length (s) with angle (θ)
• Linear velocity (v) with angular velocity (ω)
• Linear acceleration (a) with angular acceleration (α)
Remember: angles must be in radians for these formulas to
work!

5. Visualizing the Circle: The Radian
A radian is the angle where the arc length equals the radius of
the circle.
Natural Unit
Radians are the natural unit for angular measurement in
physics.
Conversion
180° = π radians
1 radian 57.3°
≈

6. Example: Rotating Arm While Standing
The Physics
When your arm swings through angle θ, your hand travels
along an arc.
Where r = length from shoulder to hand (typically 0.6-0.7m for
adults).
Shoulder Rotates
Joint creates angular motion (θ)
Arm Acts as Radius
Distance from joint to hand (r)
Hand Travels Distance
Linear distance along arc (s)

7. Exercise: Arm Circles
(Demonstration)
Stand with arm extended
Your shoulder is the pivot point (center of rotation)
Rotate arm in circles
Your hand moves in a circular path with radius r = arm length
Observe speed differences
Notice: longer arm (larger r) creates faster hand speed (v = rω)
This simple exercise demonstrates how angular motion at the joint creates
linear motion at the hand.

8. Linear and Angular Velocity: Arm Example
Example Calculation
If shoulder rotates at angular velocity ω = 1 rad/s:
Shoulder
Angular velocity (ω) = 1 rad/s
Linear velocity 0 m/s (at axis of rotation)
≈
Elbow
r 0.3 m from shoulder
≈
v = 0.3 m/s
Hand
r 0.7 m from shoulder
≈
v = 0.7 m/s

9. Gymnastics: Somersaults
In a somersault, the entire body rotates around the center of
mass.
This is pure angular motion, but creates linear motion at the
extremities.
Taller Gymnast
Greater distance (r) from
center to head/feet
Higher linear velocity at
extremities
Shorter Gymnast
Smaller distance (r) from
center to head/feet
Lower linear velocity at
extremities

10. Dance: Pirouette Spin
Arms Extended
Larger radius (r)
Slower angular velocity (ω)
Arms Pulled In
Smaller radius (r)
Faster angular velocity (ω)
Conservation Law
Angular momentum stays constant: L = Iω
As I decreases, ω increases
This demonstrates conservation of angular momentum, which connects to
our linear-angular relationships.

11. Linking Concepts with a Hula Hoop
A hula hoop provides a perfect example of circular motion
around a central axis.
Where r = radius of the hoop, typically 0.4-0.5m.
Center (Waist)
Acts as the axis of rotation
Has angular motion only (ω)
Hoop Rim
Moves with linear velocity v = rω
Every point on the hoop has the same angular velocity

12. Partner Activity: Spinning vs. Running
Spinning Student
High angular velocity (ω)
Zero linear velocity at center
Increasing linear velocity moving outward from center (v = rω)
Running Student
High linear velocity (v)
Zero angular velocity (ω = 0)
All body parts move at approximately the same linear speed
Compare these movements to see the difference between pure linear and pure angular motion.

13. Jumping Jacks: Hands' Paths
The Motion
During jumping jacks, your hands move in arcs centered at your
shoulders.
This creates both angular and linear motion simultaneously.
1
Starting
Position
Arms at sides, θ = 0
2 Middle
Position
Arms horizontal, θ =
π/2 rad (90°)
3
Full Extension
Arms overhead, θ =
π rad (180°)
Distance hands travel: s = rθ, with r = length from shoulder to
hand

14. Measuring Angular
Displacement: Smartphone
Demo
Get a smartphone with gyroscope
Most modern phones have this sensor built in
Download a sensor app
Many free apps can display gyroscope readings in real time
Perform a turn or spin
Measure the angular displacement (θ) in degrees or radians
Calculate distance traveled
Use s = rθ, where r = distance from spin center to phone

15. Cartwheel Example: Full Body Rotation
Linear Motion
During a cartwheel, your center of mass follows a relatively straight path.
This creates linear displacement from one point to another.
Angular Motion
Simultaneously, your limbs rotate around multiple joints.
Each limb follows its own circular arc with radius r = joint-to-extremity length.
Body Rotation
Full 360° (2π rad) rotation around longitudinal
axis
Arm Motion
Rotates at shoulder joint with r = arm length
Leg Motion
Rotates at hip joint with r = leg length

16. The Bicycle Wheel Analogy
Same Angular Velocity (ω)
Every point on a spinning bicycle wheel rotates at the same
angular velocity.
All points complete one revolution in the same time.
Different Linear Velocities (v)
Linear velocity depends on distance from center: v = rω

17. Real-World Application: Sports
Baseball Bat
Rotates around a pivot point (hands)
Bat tip moves much faster than handle
(v = rω)
This generates more impact force at
the "sweet spot"
Soccer Kick
Leg rotates around hip joint
Foot moves in an arc with r = leg
length
Linear velocity at foot (v = rω) transfers
to ball

18. Activity: Create Your Own Example
Choose a movement
Simple examples: waving an arm, twirling a ribbon, swinging a leg
Identify components
Measure r (radius) from rotation center to end point
Measure angle
Use protractor or smartphone to measure angular displacement (θ)
Calculate
Find arc length (s = rθ) or linear velocity (v = rω)
Present findings
Demonstrate your movement and explain the physics behind it

19. Summary of Linear-Angular Relationships
Key Relationships
These formulas connect the angular world with the linear world.
Displacement
Arc length (s) depends on angle (θ) and radius (r)
Velocity
Linear speed (v) depends on angular speed (ω) and
radius (r)
Acceleration
Linear acceleration (a) depends on angular acceleration
(α) and radius (r)

20. Conclusion: Why These Relationships Matter
Exercise Science
Understanding joint mechanics helps
prevent injuries and optimize
movement.
Performance Optimization
Athletes and dancers use these
principles to increase speed and
efficiency.
Physics Education
Human movement provides intuitive
examples of abstract physics concepts.
Everyday Applications
These relationships explain how tools
and machines work in daily life.
By connecting these concepts to human movement, we make physics relevant and accessible!