Dive into the fascinating world of motion with this educational presentation that compares translational and rotational motion—two fundamental concepts in physics. Designed for students, educators, and science enthusiasts, this SlideShare breaks down the similarities and differences between these types of motion in a clear and engaging way. 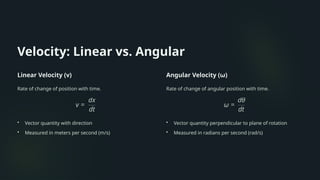⚙️ Key topics covered: Definitions and real-life examples of translational and rotational motion Core concepts such as displacement, velocity, acceleration, and force Analogies between linear and angular quantities (e.g., mass vs. moment of inertia) Equations of motion and how they apply in each case Practical applications in engineering, sports, and everyday life Through diagrams, comparisons, and simplified explanations, this presentation helps viewers understand how objects move in straight lines and how they rotate around axes—and why both types of motion are essential in understanding the physical world. 📘 Perfect for physics learners looking to strengthen their grasp of mechanics and motion!

1. Comparing Translational
and Rotational Motion
Discover the fundamental relationships between linear and angular
motion in mechanics. We'll explore how objects move in straight lines
and in circles, and the mathematical connections between these two
types of motion.
by ANGELIQUE TOLENTINO DEL ROSARIO

2. What is Translational Motion?
Translational motion occurs when an object moves from
one location to another along a straight path.
This is the simplest form of motion we observe in everyday life.
Linear Displacement
Change in position measured in meters (m)
Linear Velocity
Rate of change in position (m/s)
Linear Acceleration
Rate of change in velocity (m/s²)

3. What is Rotational Motion?
Rotational motion describes movement around a fixed axis.
Objects follow a circular path rather than a straight line.
Angular Displacement
Change in angle measured in radians (rad)
Angular Velocity
Rate of change in angle (rad/s)
Angular Acceleration
Rate of change in angular velocity (rad/s²)

4. Path and Reference Point
Translational Motion
Objects follow straight-line paths. Position is measured
relative to a fixed reference point in space.
Rotational Motion
Objects move in circular paths. Position is measured as an
angle relative to an axis of rotation.

5. Units and Measurements
Quantity Type Translational Rotational
Displacement Meters (m) Radians (rad)
Velocity Meters per second (m/s) Radians per second (rad/s)
Acceleration Meters per second squared (m/s²) Radians per second squared (rad/s²)
Force/Torque Newtons (N) Newton-meters (N·m)
Different units reflect the fundamental differences between linear and angular measurements.

6. Displacement: Linear vs.
Angular
Linear Displacement (x)
The change in position of an object measured along a straight line.
Measured in meters (m)
Angular Displacement (θ)
The angle through which an object rotates around an axis.
Measured in radians (rad)

7. Velocity: Linear vs. Angular
Linear Velocity (v)
Rate of change of position with time.
• Vector quantity with direction
• Measured in meters per second (m/s)
Angular Velocity (ω)
Rate of change of angular position with time.
• Vector quantity perpendicular to plane of rotation
• Measured in radians per second (rad/s)

8. Acceleration: Linear vs. Angular
Linear Acceleration (a)
Rate of change of velocity with time.
Measured in meters per second squared (m/s²)
Angular Acceleration (α)
Rate of change of angular velocity with time.
Measured in radians per second squared (rad/s²)

9. Position Equations: Analogy
Overview
1 Translational Position
Current position equals initial position plus velocity multiplied by time.
2 Rotational Position
Current angle equals initial angle plus angular velocity multiplied by time.
Notice the perfect symmetry between these equations. Each translational term has
an angular counterpart.

10. Velocity and Acceleration Equations
Translational Motion
Final velocity equals initial velocity plus acceleration
multiplied by time.
Example: A car accelerating from rest reaches 20 m/s after
10 seconds of constant acceleration.
Rotational Motion
Final angular velocity equals initial angular velocity plus
angular acceleration multiplied by time.
Example: A spinning top accelerates from rest to 10 rad/s in
5 seconds.

11. Position with Constant
Acceleration
1 Translational Position Formula
The quadratic term accounts for distance covered during acceleration.
2 Rotational Position Formula
The same pattern applies to angular position with constant angular acceleration.
These equations reveal the deep mathematical symmetry between translational
and rotational motion.

12. Final Velocity Squared Equations
Translational Motion
This equation relates final velocity to initial velocity,
acceleration, and displacement without using time.
Rotational Motion
The angular equivalent follows the same pattern, relating
angular velocity change to angular displacement.
These equations are especially useful when time isn't known but displacement is.

13. Momentum: Linear vs.
Angular
Linear Momentum (p)
A product of mass and velocity. Describes an object's tendency to
continue moving in a straight line.
Units: kg·m/s
Angular Momentum (L)
A product of moment of inertia and angular velocity. Describes an
object's tendency to continue rotating.
Units: kg·m²/s

14. Mass vs. Moment of Inertia
Mass (m)
A measure of an object's resistance to linear acceleration.
Mass is a scalar quantity that doesn't depend on position or
orientation.
Units: kilograms (kg)
Moment of Inertia (I)
A measure of an object's resistance to angular acceleration.
Depends on mass distribution relative to the axis of rotation.
Units: kilogram-meters squared (kg·m²)

15. Force vs. Torque
Force (F)
Causes linear acceleration
according to Newton's Second Law.
Force is a vector with magnitude
and direction.
Torque (τ)
Causes angular acceleration in
rotational motion.
Torque depends on force, distance
from axis, and angle of application.

16. Energy: Linear vs.
Rotational
KE
Translational Kinetic
Energy
Energy of motion for an object
moving in a straight line.
KE
Rotational Kinetic Energy
Energy of motion for a rotating
object.
The total kinetic energy of an object can be the sum of both
translational and rotational components.

17. Linking Linear and Angular
Quantities
Velocity Relationship
Linear velocity equals radius multiplied by angular velocity.
Points farther from the axis move faster linearly while having the same
angular velocity.
Acceleration Relationship
Linear acceleration equals radius multiplied by angular acceleration.
Points farther from the axis experience greater linear acceleration.

18. Physical Examples
Translational Motion Examples
• Car moving on a straight road
• Ball thrown through the air
• Train moving along tracks
• Elevator moving up and down
Rotational Motion Examples
• Spinning bicycle wheel
• Earth rotating on its axis
• Clock hands moving
• Fan blades turning
These everyday examples help us visualize the difference between the two types of motion.

19. General Motion: Combination of Both
Rolling Motion
A perfect example of combined translational and rotational motion.
The center moves in a straight line while the object rotates around its axis.
Complex Motion
Objects like gyroscopes demonstrate complex combinations of
rotational motions around multiple axes.
Spinning tops and planets exhibit similar complex behaviors.

20. Summary and Key Takeaways
Mathematical Parallels
Each linear quantity has an angular
counterpart with the same
mathematical structure.
Interconnected
Relationships
Linear and angular quantities are
connected through the radius: v = rω
and a = rα.
Equation Patterns
Rotational motion equations mirror
translational forms, replacing x with
θ, v with ω, and a with α.
Practical Applications
Understanding these parallels
simplifies problem-solving in
mechanics and engineering.