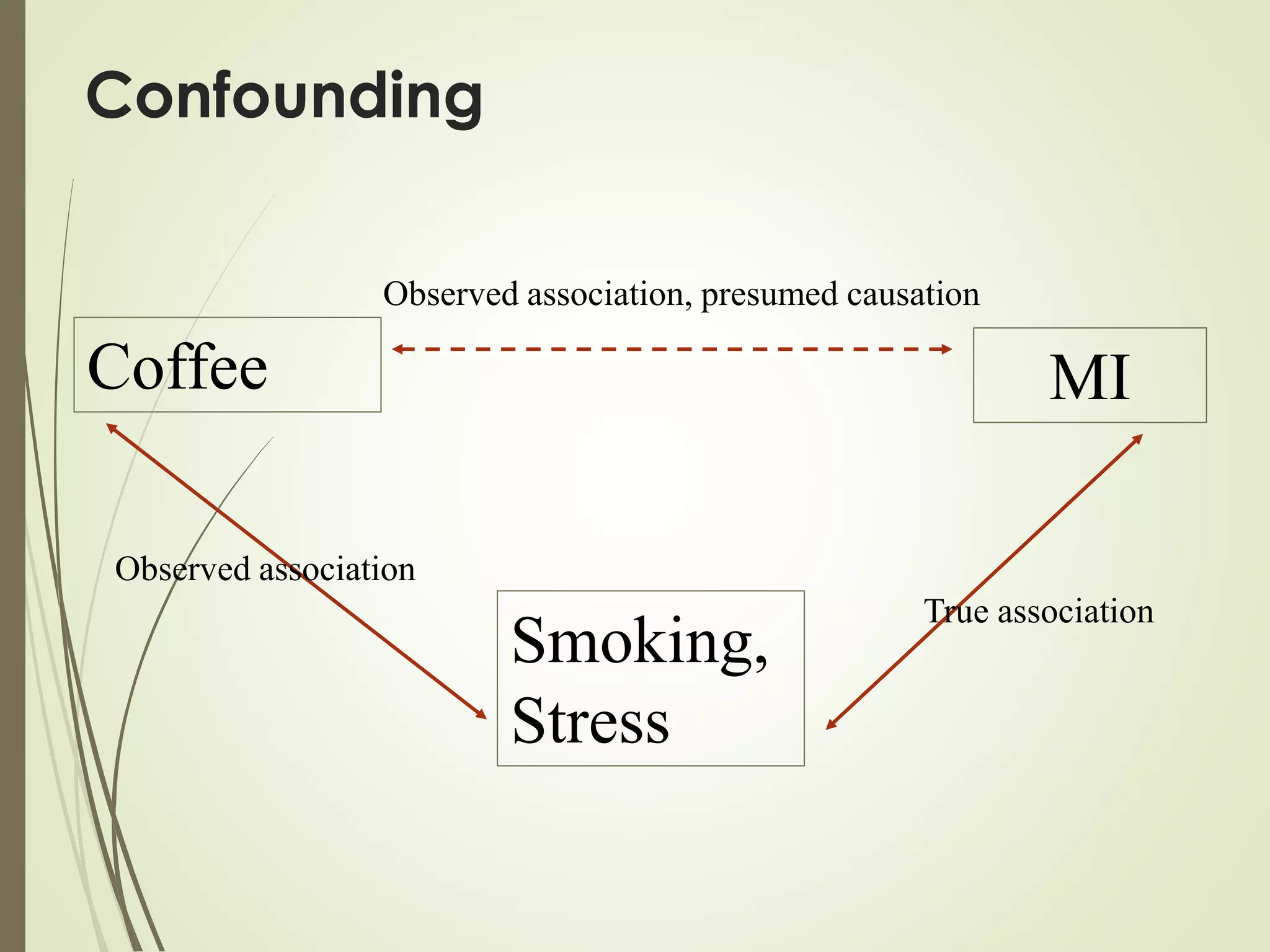
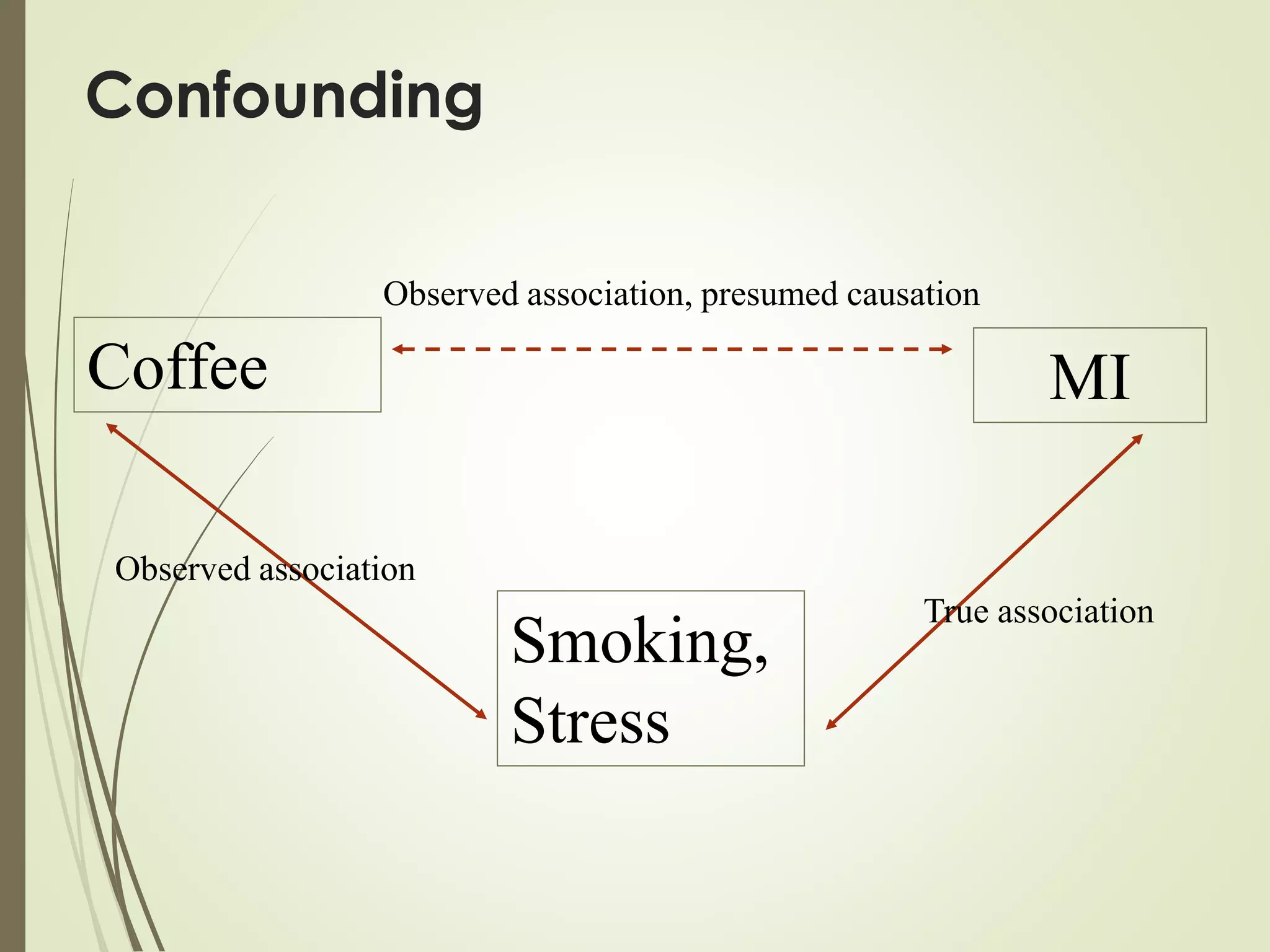
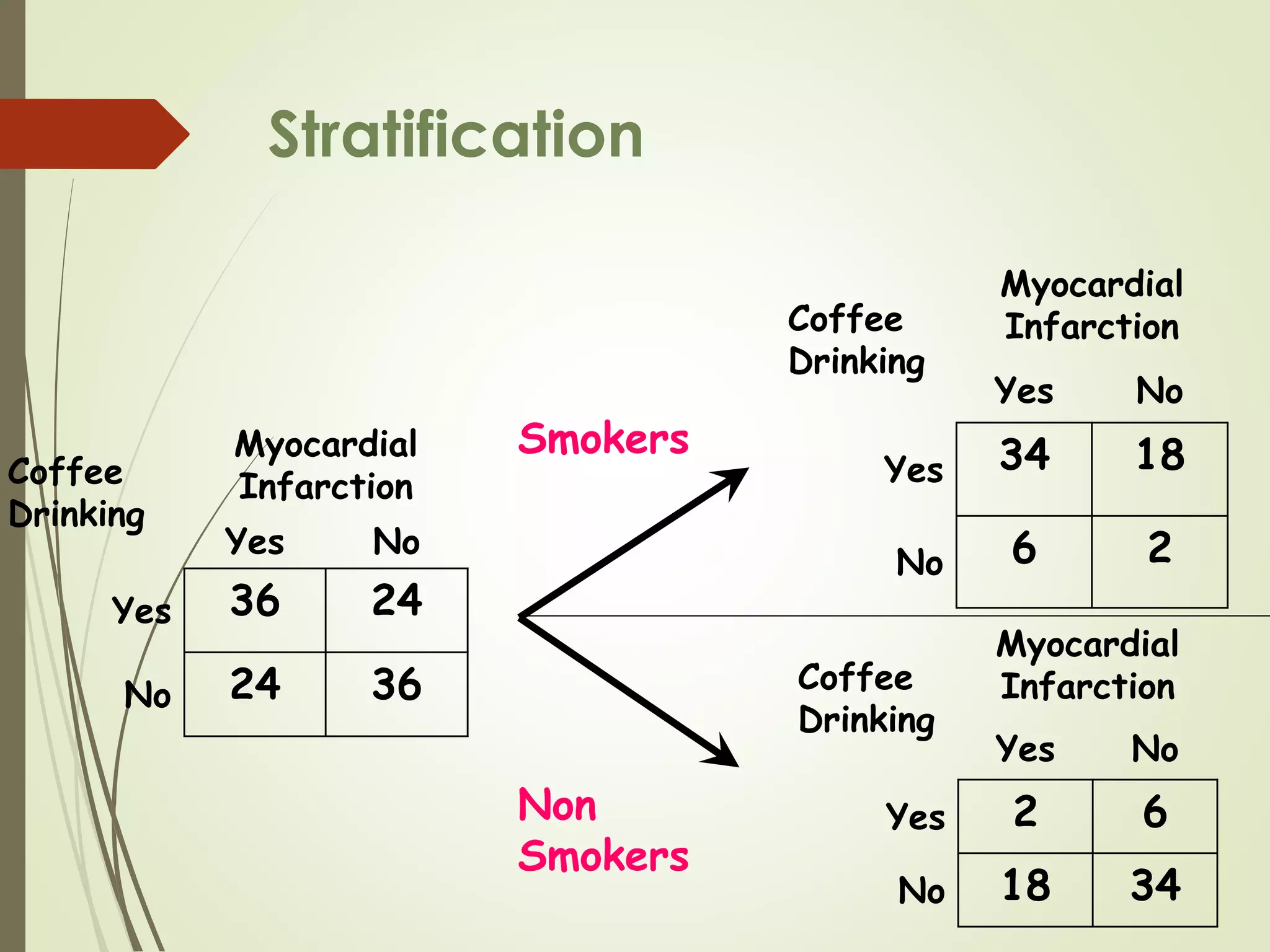
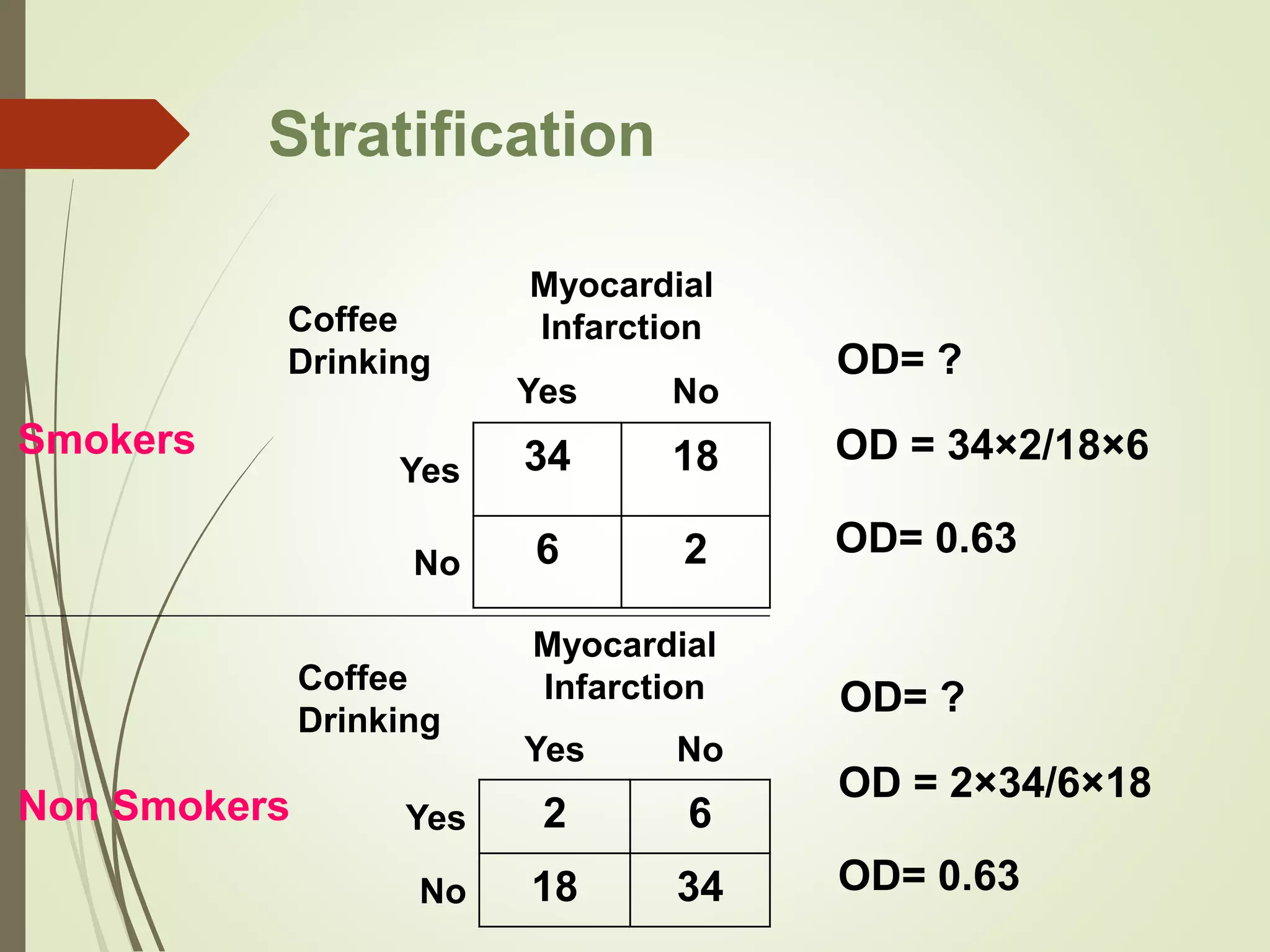
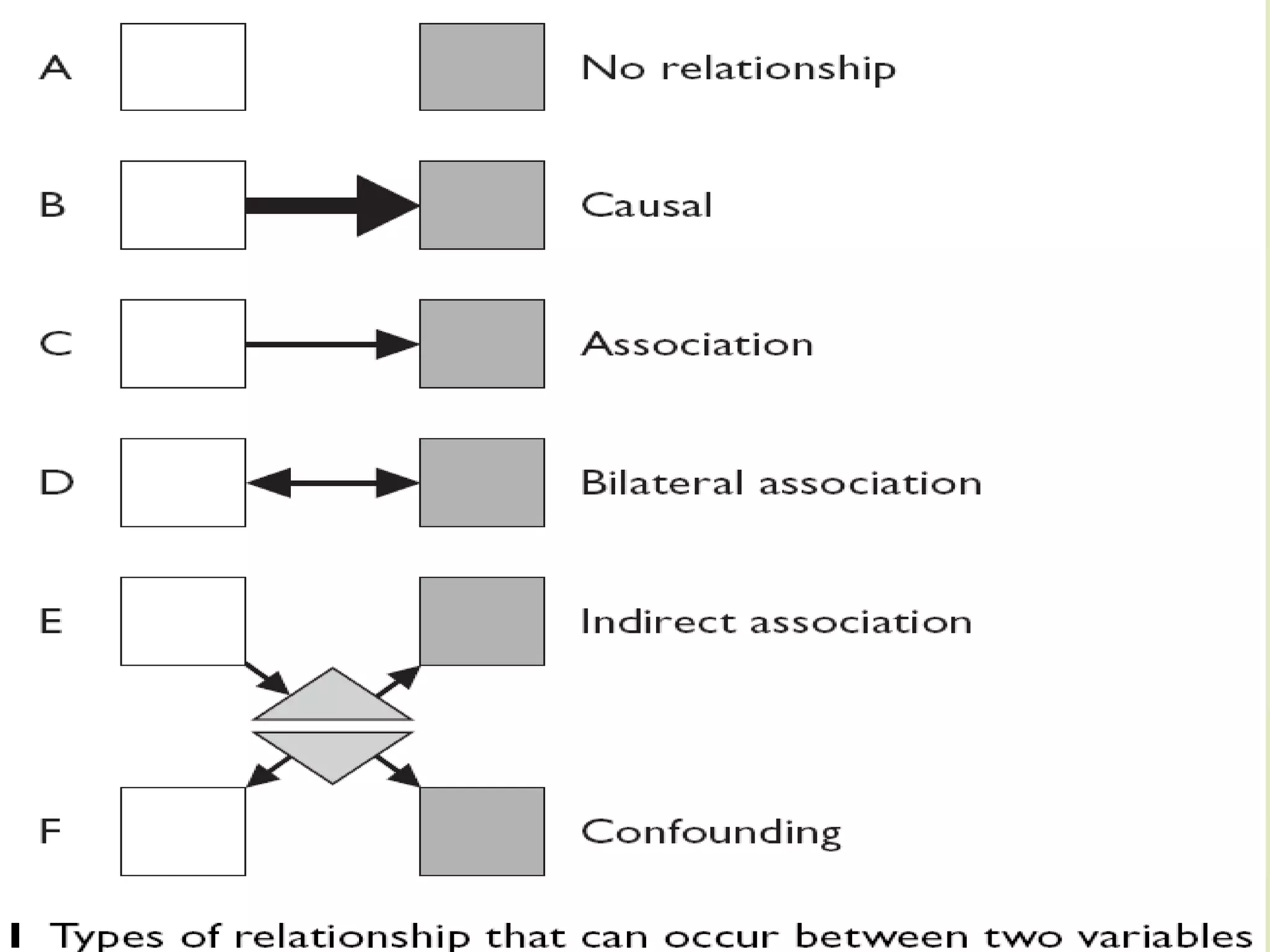
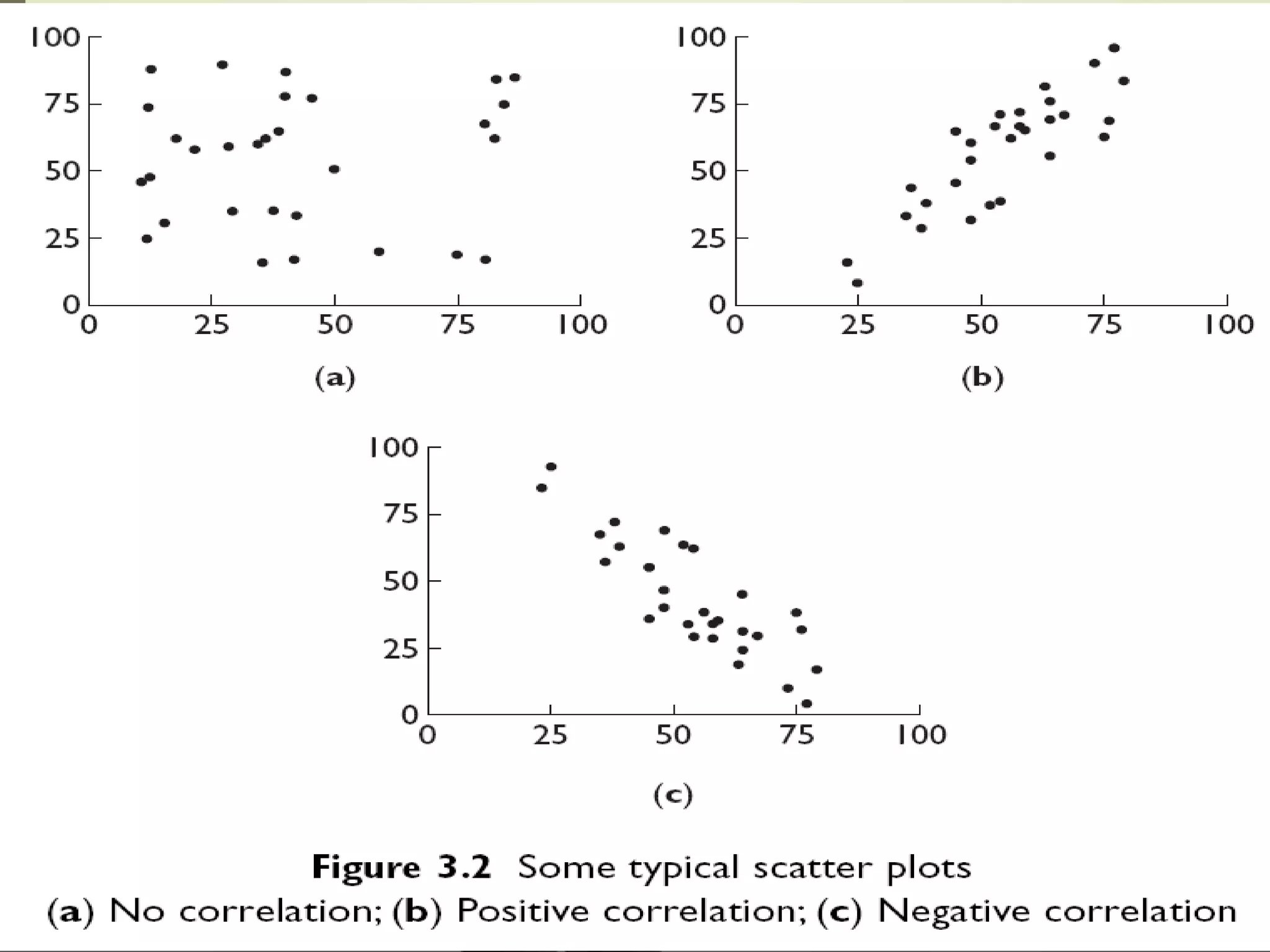
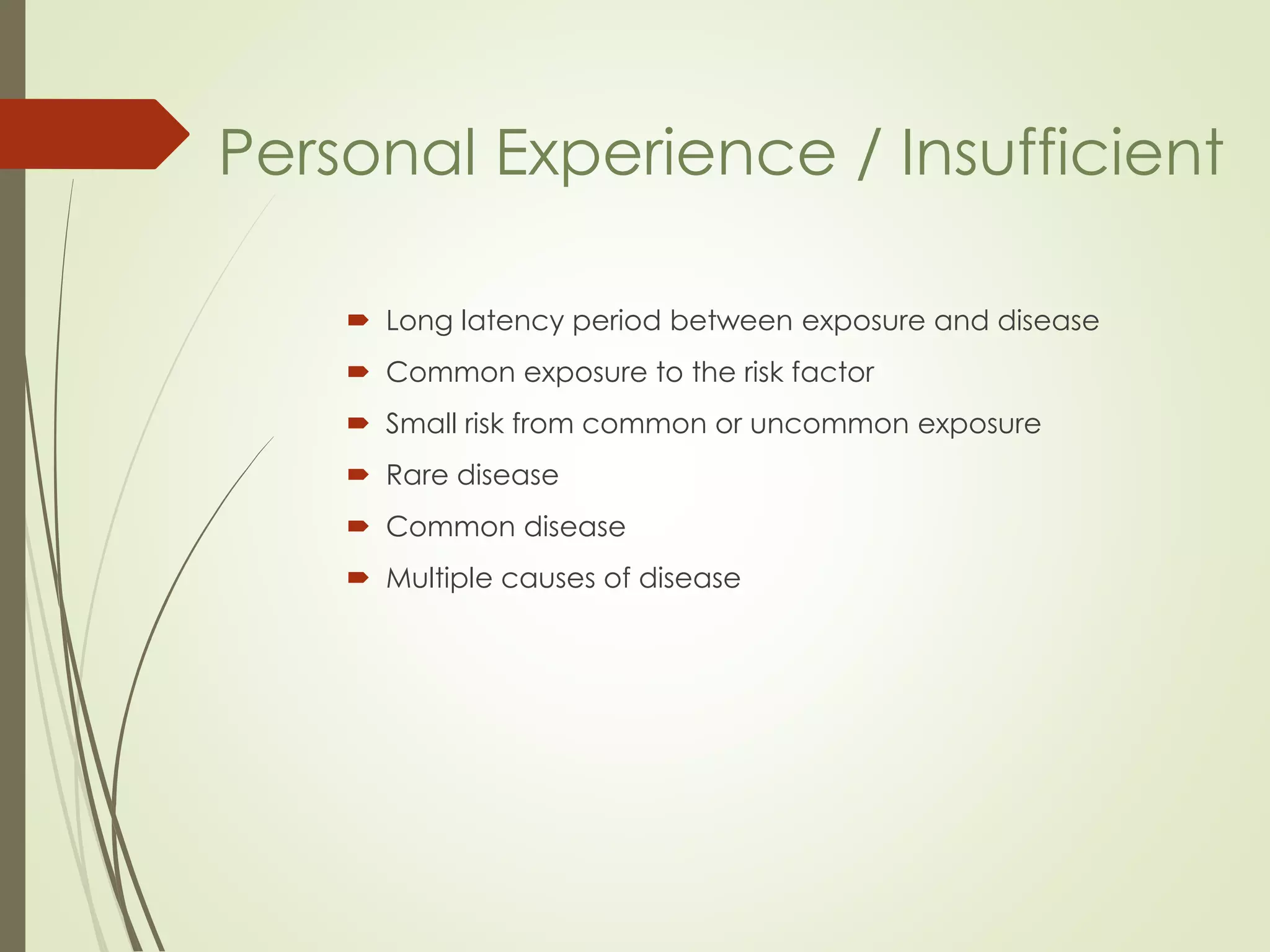
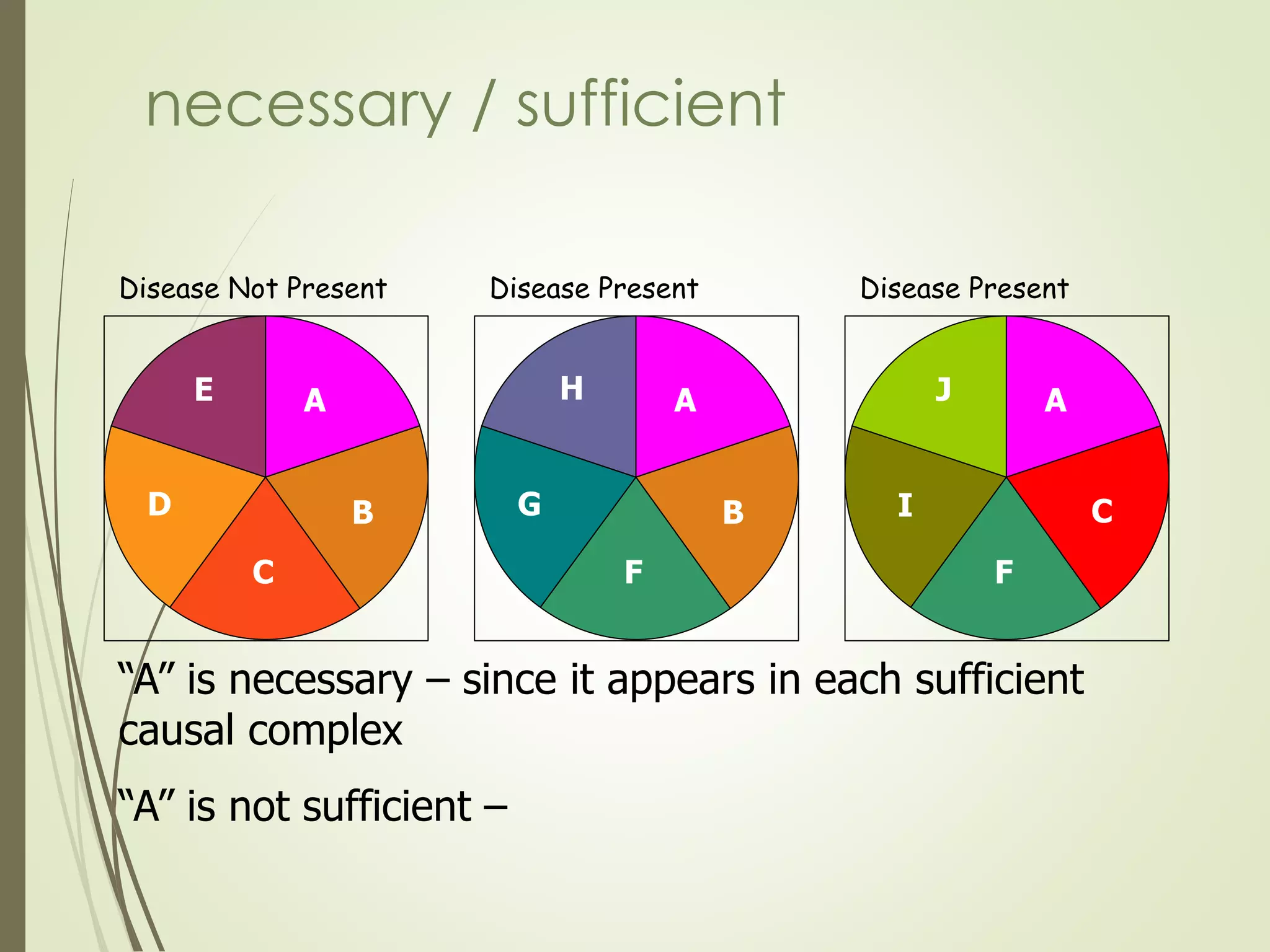
This document discusses the concepts of association versus causation in epidemiology. It defines association as events occurring together more frequently than expected by chance, while causation requires proving a direct causal relationship. The document outlines different types of associations and discusses how associations can be due to chance, bias, confounding or true causation. It also discusses various criteria for establishing causality such as strength of association, consistency of findings, temporal relationship, dose-response relationship, and consideration of alternative explanations.