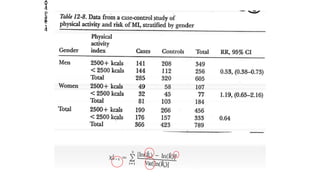
This document discusses effect modification and how it differs from confounding. It defines effect modification as a change in the magnitude of the effect of an exposure on an outcome according to levels of a third variable. Effect modification provides a more detailed description of the relationship between exposure and outcome, whereas confounding is a bias to be eliminated. The document contrasts effect modification and confounding, and provides examples to illustrate the concepts. It also discusses testing for effect modification using tests of homogeneity and how the interpretation of effect modification depends on the choice of effect measure.

1. 2014
Page
1
68
Effect modification (Interaction)
• Goals of stratification of data
– Evaluate and reduce/remove confounding
– Evaluate and describe effect modification
• Description of effect modification
– A change in the magnitude of an effect measure
(between exposure and disease) according to the level
of some third variable
– What two “classes” of effect measures have we used so
far in the course?

2. exampleEffect modification:
#1
• Disease incidence by exposure and age
– Does the relationship between exposure and disease change
over the value of the potential confounder (age)? How?
69
2014
Page
2

3. Effect modification: example #2
• Disease incidence by exposure and age
• Does the relationship between exposure and disease
change over the value of the potential confounder
(age)? How?
Rothman ’86 (p 178)
2014
Page
3
70

4. 2014
Page
4
contrastEffect modification:
with confounding
• Confounding
– A bias that an investigator hopes to remove
– A nuisance that may or may not be present in a given
study design
• Properties of a confounding variable: (Rothman, p123):
– a) be a risk factor for disease among the non-exposed;
– b) be associated with the exposure variable; and
– c) not be an intermediate step in the “causal pathway”
71

5. 2014
Page
5
contrastEffect modification:
with confounding
• Effect modification
– A more detailed description of the “true” relationship
between the exposure and the outcome
– Effect modification is a finding to be reported (even
celebrated), not a bias to be eliminated
– Effect modification is a “natural phenomenon” that
exists independently of the study design
– The presence and interpretation of effect modification
depends upon the choice of effect measure (ratio vs.
difference)
72

6. 2014
Page
6
73
Some lingo
• Covariate
– Confounder, potential confounder
– Effect modification, interaction
– Intermediate variable

7. 2014
Page
7
Effect modification: contrast
with confounding
• Note that for any association under study, a given factor
may be:
– Both a confounder and an effect modifier or
– A confounder but not an effect modifier or An effect
modifier but not a confounder or
– neither
74

8. 2014
Page
8
Examples of confounding/effect
modification
76
Level 1 Level 2 Crude/
collapsed/
Combined
“unadjusted
”
Uniform
estimate
(ORMH)
/
“adjusted”
Confounding
present
Interaction
present
4.0 4.0 4.0 4.0 NO NO
4.0 0.25 1.0 1.0 NO YES
1.0 1.0 8.4 1.0 YES NO
4.0 0.25 1.0 2.0 YES
(?relevance)
YES

9. 77
2014 Page 90

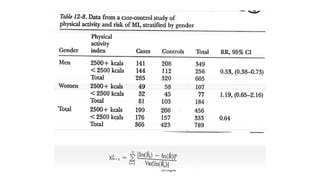
10. Effect modification: test of
homogeneity
• Null hypothesis: The individual stratified estimates of the effect do not
differ from some uniform estimate of effect (such as a Mantel Haenszel
estimator)
• Notation:
– N is the number of strata (N=2 in our smoking/matches example);
–
MH
ln^Ri is the natural logarithm of the estimated (hence the “^”) effect
measure for each stratum (ORi in our example);
– ln^R is the natural logarithm of the uniform effect estimate (e.g. OR in
– X2
(N-1)
is chi-square with (N-1) degrees of freedom;
our example—the computer will use the maximum likelihood estimate)
• One formula to test homogeneity:
X2
(N-1)
= ∑ [ln(^ Ri) – ln(RMH)]2
Var[ln(^
Ri)]
N
i= 1
78
JC: Comment on choice of signifciance level for test of homogeneity
2014
Page
10

11. 2014
Page
11
Paradox
• If effect modification is present, a uniform estimator of
effect (such as ORMH) cannot (or at least should not) be
reported.
• However, in order to determine if effect modification is
present, it is necessary to calculate the value of a uniform
estimator of effect (such as ORMH) because it is needed in
the calculation of the test of homogeneity.
79

12. 2014
Page
12
Effect modification: test of homogeneity
(or
is heterogeneity?)
• Comments
– If the test of homogeneity is “significant” (=“reject homogeneity”)
this is evidence that there is heterogeneity (i.e. no homogeneity)
and that effect modification may be present.
• (Null hypothesis: The individual stratified estimates of the
effect do not differ from some uniform estimate of effect)
– The choice of a significance level (e.g. p < 0.05) is somewhat open
to interpretation.
• One “conservative” approach, because of inherent limitations in
the power of the test of homogeneity, is to treat the data as if
interaction is present for p < 0.20).
• In other words, one would rather err on the side of assuming
that interaction is present (and reporting the stratified estimates
of effect) than on reporting a uniform estimate that may not be
true across strata.
80

13. UC Berkeley
34
2014
Page
13

14. 81
2014
Page
14

15. Additive versus multiplicative scale effect modification
● Notation: RXZ
● No additive interaction if (R11 – R01) = (R10 – R00)
○ Rewrite as: (R11-R01)-(R10-R00)=0
● In words: Difference in risk for (X=1 vs. X=0) when Z=1 is
equal to difference in risk for (X=1 vs. X=0) when Z=0
● Note: the values R11, R10, etc. are risks (not counts)
2014
Page
15

16. Additive versus multiplicative scale effect modification
● Notation: RXZ
● No multiplicative interaction if (R11/R01)=(R10/R00)
Rewrite as: (R11/R01)/(R10/R00)=1
● In words: Ratio of risks/rates when X=1 vs. X=0 when
Z=1 is equal to ratio of risks/rates when X=1 vs. X=0
when Z=0
2014
Page
16

17. 2014
Page
17 Effect modification is scale-dependent
•Evidence for effect modification/statistical interaction
if the RR or the AR differs between two groups
•However, effect modification/statistical interaction is
scale-dependent
–If you do not have interaction on the additive scale (AR is
homogenous) then you will have interaction on the multiplicative
scale (RR must be heterogeneous)
–If you do not have interaction on the multiplicative scale (RR is
homogenous) then you will have interaction on the additive scale
(AR must be heterogeneous)
–Note: It is common to have evidence of interaction on both
scales.

18. Example
● No additive scale interaction if (R11-R01)-(R10-R00)=0
● No relative scale interaction if (R11/R01)/(R10/R00)=1
● Additive scale: (60-20) - (50-10) = 0
○ Interaction not present on the additive scale
● Relative scale: (60/20) / (50/10)=0.6
○ Interaction present on the relative scale
Z=1 Z=0
X=1 60 50
X=0 20 10
2014
Page
18

19. Example
● No additive scale interaction if (R11-R01)-(R10-R00)=0
● No relative scale interaction if (R11/R01)/(R10/R00)=1
● Additive scale: (60-20) - (30-10) = 20
○ Interaction present on the additive scale
● Relative scale: (60/20) / (30/10)=1
○ Interaction not present on the relative scale
Z=1 Z=0
X=1 60 30
X=0 20 10
2014 Page 100