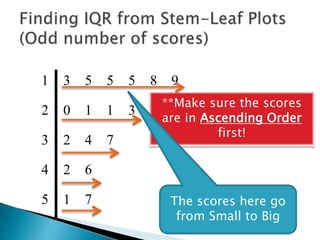
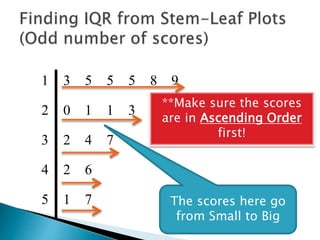
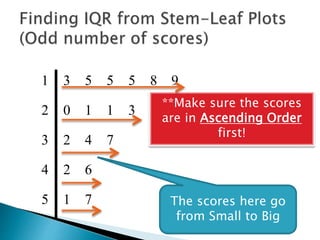
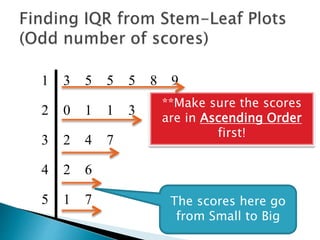
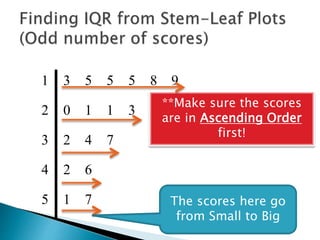
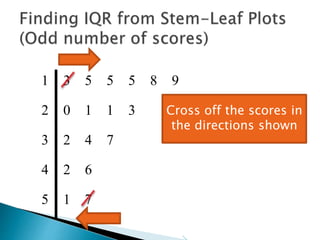
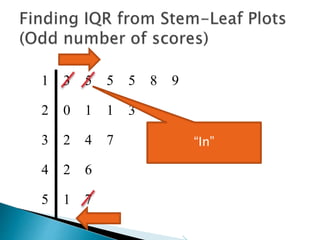
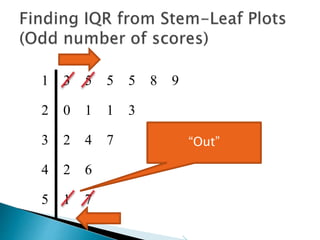
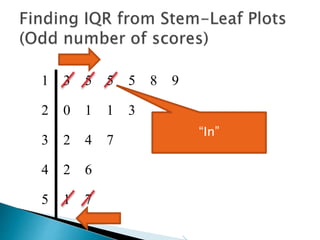
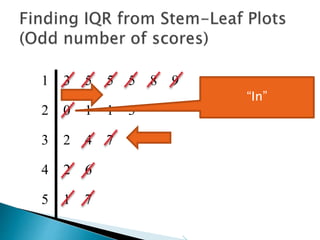
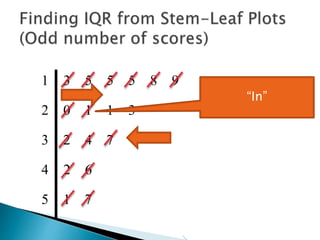
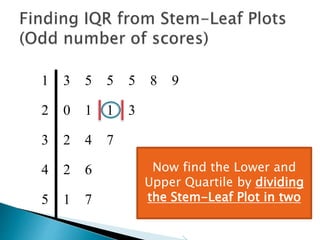
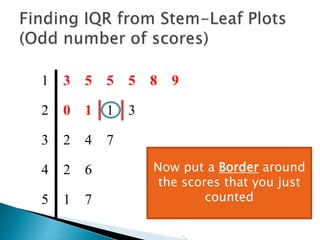
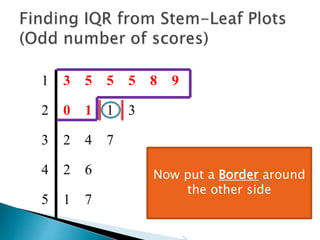
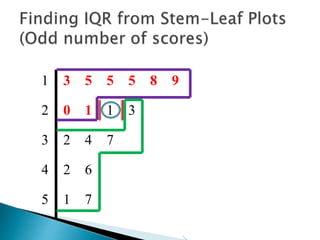
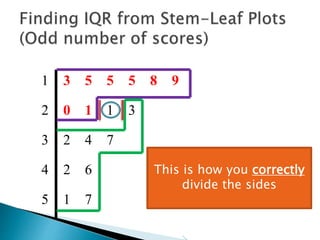
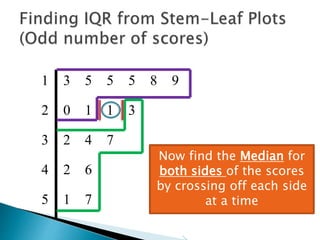
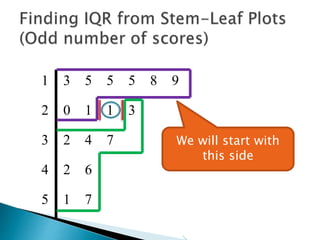
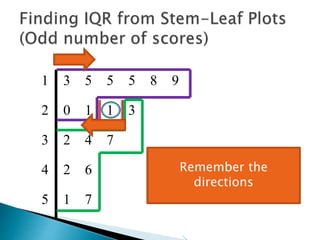
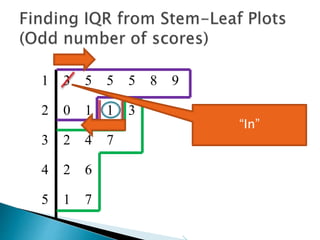
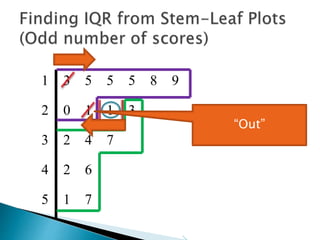
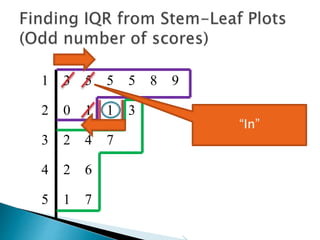
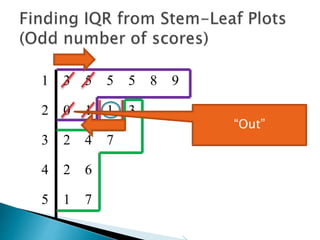
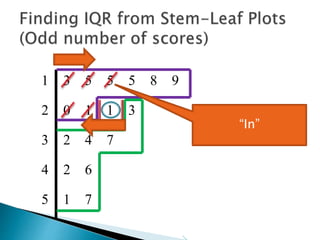
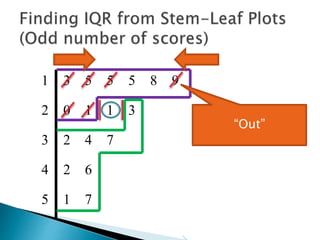
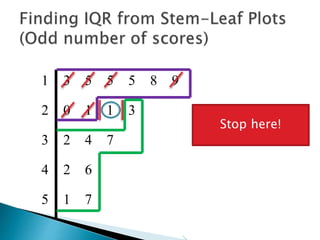
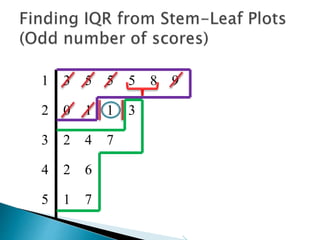
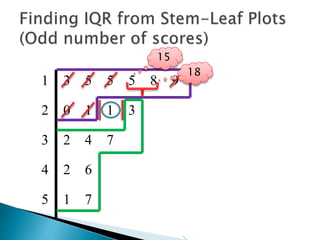
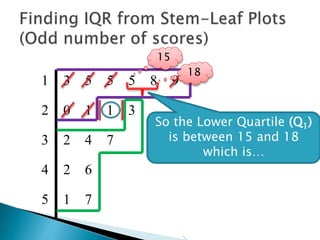
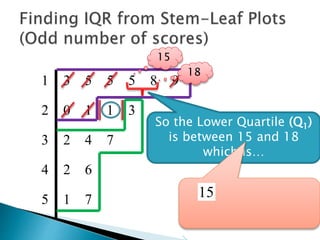
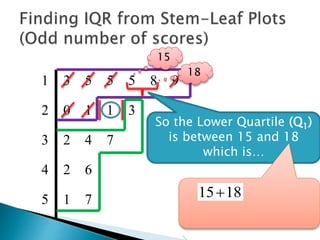
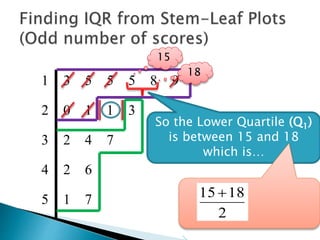
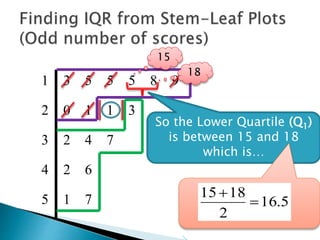
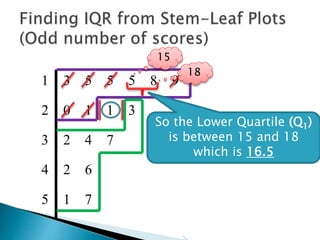
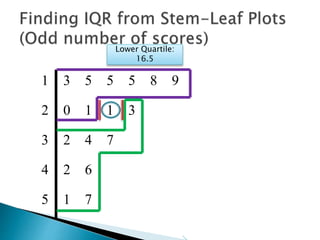
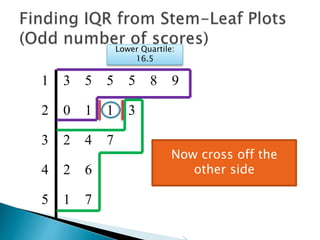
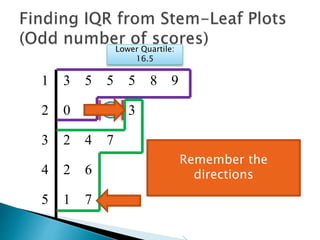
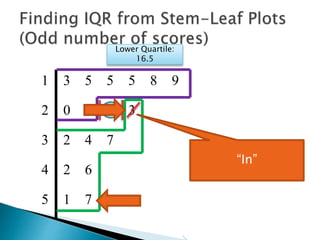
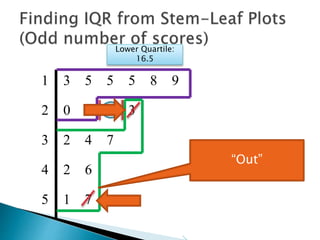
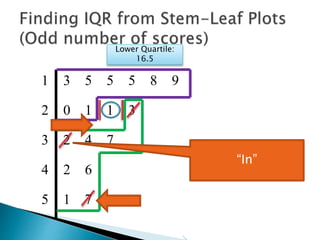
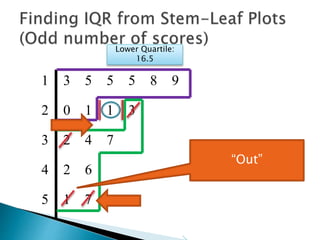
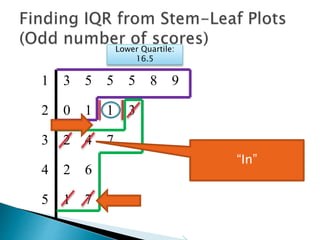
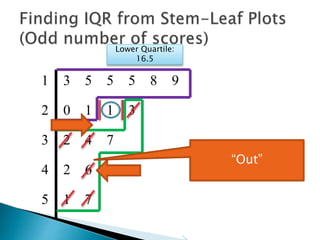
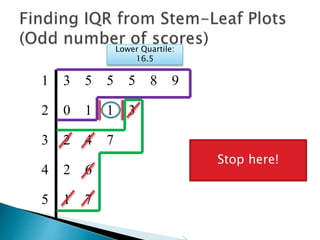
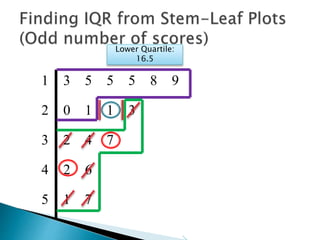
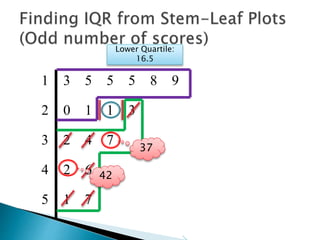
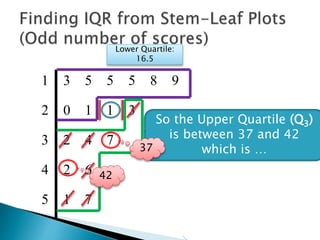
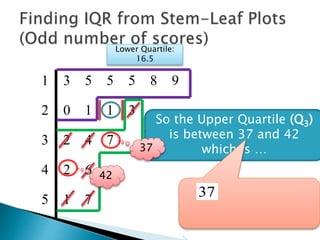
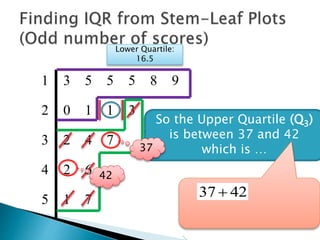
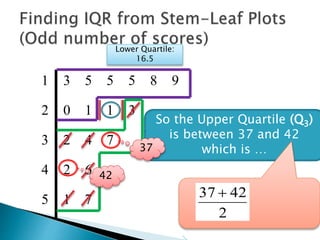
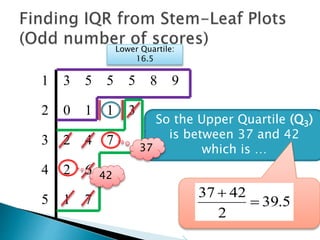
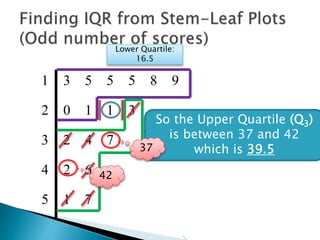
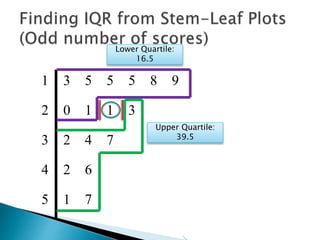
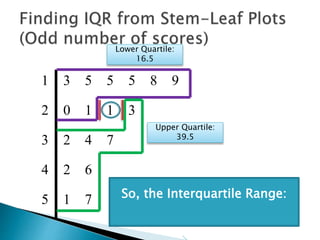
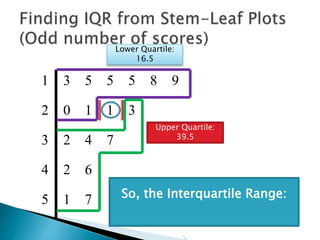
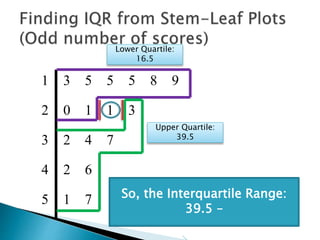
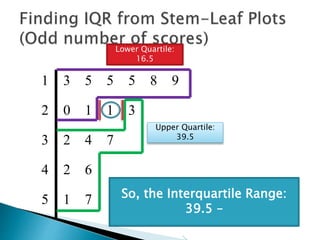
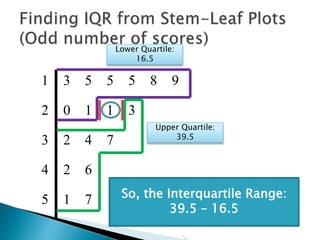
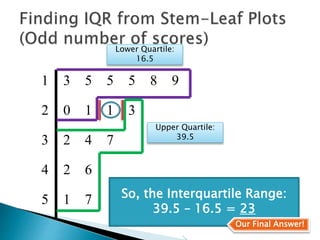
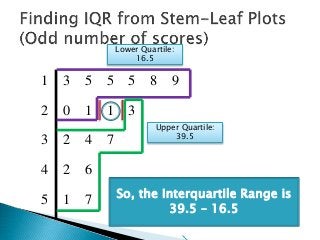
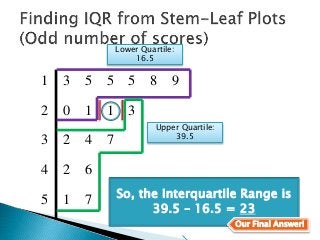
This document provides instructions for finding the interquartile range (IQR) of a data set with an odd number of values. It explains how to order the data from smallest to largest, find the median by crossing out values from the top and bottom, and divide the remaining values into two sides to separately calculate the lower and upper quartiles.

1. - Mr Kim

2. Finding IQR for odd number of scores

3. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7

4. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
First, find the Median by
crossing off the scores

5. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
**Make sure the scores
are in Ascending Order
first!

6. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
**Make sure the scores
are in Ascending Order
first!

7. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
**Make sure the scores
are in Ascending Order
first!
The scores here go
from Small to Big

8. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7 The scores here go
from Small to Big
**Make sure the scores
are in Ascending Order
first!

9. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7 The scores here go
from Small to Big
**Make sure the scores
are in Ascending Order
first!

10. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7 The scores here go
from Small to Big
**Make sure the scores
are in Ascending Order
first!

11. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7 The scores here go
from Small to Big
**Make sure the scores
are in Ascending Order
first!

12. 1 5 3 5 8 5 9
2 3 0 1 3
3 2 7 4
4 2 6
5 1 7
For example this is not
in ascending order

13. 1 5 3 5 8 5 9
2 3 0 1 3
3 2 7 4
4 2 6
5 1 7
For example this is not
in ascending order

14. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Now, start by crossing
off the Smallest Number

15. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
13
Now, start by crossing
off the Smallest Number

16. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7

17. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Now cross off the
Biggest Number

18. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
57
Now cross off the
Biggest Number

19. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7

20. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Cross off the scores in
the directions shown

21. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
“In”

22. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
“Out”

23. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
“In”

24. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
“Out”

25. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
“In”

26. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
“Out”

27. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
“In”

28. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
“Out”

29. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
“In”

30. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
“Out”

31. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
“In”

32. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
“Out”

33. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
“In”

34. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
“Out”

35. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Stop here

36. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Always stop at “Out”

37. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
So the Median (Q2)
is…

38. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
So the Median (Q2) is
21

39. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Now put 2 lines
around it like shown

40. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Now find the Lower and
Upper Quartile by dividing
the Stem-Leaf Plot in two

41. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
**It is very important to
divide the sides properly

42. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
To do this, count the
scores from the start
until you reach the Line

43. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7

44. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7

45. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7

46. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7

47. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7

48. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7

49. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7

50. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7

51. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Stop here!

52. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Now put a Border around
the scores that you just
counted

53. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7

54. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Now put a Border around
the other side

55. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7

56. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
This is how you correctly
divide the sides

57. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Now find the Median for
both sides of the scores
by crossing off each side
at a time

58. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
We will start with
this side

59. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Remember the
directions

60. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
“In”

61. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
“Out”

62. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
“In”

63. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
“Out”

64. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
“In”

65. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
“Out”

66. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Stop here!

67. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7

68. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
15
18

69. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
15
18
So the Lower Quartile (Q1)
is between 15 and 18
which is…

70. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
15
18
So the Lower Quartile (Q1)
is between 15 and 18
which is…
15

71. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
15
18
So the Lower Quartile (Q1)
is between 15 and 18
which is…
1815

72. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
15
18
So the Lower Quartile (Q1)
is between 15 and 18
which is…
2
1815 

73. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
15
18
So the Lower Quartile (Q1)
is between 15 and 18
which is…
5.16
2
1815



74. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
15
18
So the Lower Quartile (Q1)
is between 15 and 18
which is 16.5

75. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Lower Quartile:
16.5

76. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Now cross off the
other side
Lower Quartile:
16.5

77. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Lower Quartile:
16.5
Remember the
directions

78. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Lower Quartile:
16.5
“In”

79. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Lower Quartile:
16.5
“Out”

80. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Lower Quartile:
16.5
“In”

81. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Lower Quartile:
16.5
“Out”

82. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Lower Quartile:
16.5
“In”

83. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Lower Quartile:
16.5
“Out”

84. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Lower Quartile:
16.5
Stop here!

85. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Lower Quartile:
16.5

86. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Lower Quartile:
16.5
37
42

87. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Lower Quartile:
16.5
So the Upper Quartile (Q3)
is between 37 and 42
which is …37
42

88. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Lower Quartile:
16.5
42
So the Upper Quartile (Q3)
is between 37 and 42
which is …37
37

89. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Lower Quartile:
16.5
42
So the Upper Quartile (Q3)
is between 37 and 42
which is …37
4237 

90. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Lower Quartile:
16.5
42
So the Upper Quartile (Q3)
is between 37 and 42
which is …37
2
4237 

91. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Lower Quartile:
16.5
42
So the Upper Quartile (Q3)
is between 37 and 42
which is …37
5.39
2
4237



92. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Lower Quartile:
16.5
42
So the Upper Quartile (Q3)
is between 37 and 42
which is 39.537

93. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Lower Quartile:
16.5
Upper Quartile:
39.5

94. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Lower Quartile:
16.5
So, the Interquartile Range is
Upper Quartile:
39.5

95. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Lower Quartile:
16.5
So, the Interquartile Range is
Upper Quartile:
39.5

96. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Lower Quartile:
16.5
Upper Quartile:
39.5
So, the Interquartile Range is
39.5 –

97. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Lower Quartile:
16.5
Upper Quartile:
39.5
So, the Interquartile Range is
39.5 –

98. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Lower Quartile:
16.5
Upper Quartile:
39.5
So, the Interquartile Range is
39.5 – 16.5

99. 1 3 5 5 5 8 9
2 0 1 1 3
3 2 4 7
4 2 6
5 1 7
Lower Quartile:
16.5
So, the Interquartile Range is
39.5 – 16.5 = 23
Our Final Answer!
Upper Quartile:
39.5