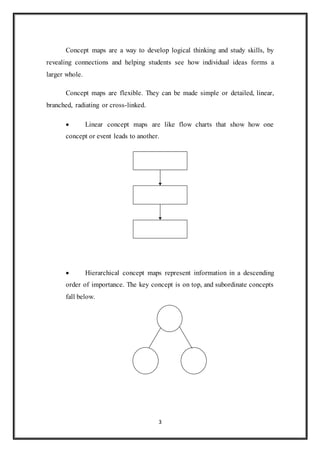
This document discusses concept mapping, simulation, and gradation as teaching techniques. It defines concept mapping as a visual way to show relationships between concepts using circles or boxes connected by words. Simulation is enacting a real situation in class to demonstrate topics like how a cooperative society works. Gradation means introducing concepts step-by-step from simple to complex so students can discover principles on their own. Examples are provided for how to implement these techniques in teaching mathematics.

1. An assignment on Concept Mapping,
Simulation and Gradation.
Assignment prepared by
Shefsyn K.Y.
Reg. No: 13 386 006
B. Ed (Mathematics)
STTC
1

2. Concept Mapping
Used to
designate
2
Introduction to Concept Mapping
Used as learning and teaching technique, concept mapping visually
illustrates the relationships between concepts and ideas. Often represented in
circles or boxes, concepts are linked by words and phrases that explain the
connection between the ideas, helping students organize the structure their
thoughts to further understand information and discover new relationships. Most
concept maps represent a hierarchical structure, with the overall, broad concept
first with connected sub-topics, more specific concepts, following.
Number
Imaginary
used in
Operations
e.g
Real
Can be
Quantities May represent
has
Different
meanings
for
Multiply
Can be
Add Linear Nonlinear Specific
Concept Map Example

3. Concept maps are a way to develop logical thinking and study skills, by
revealing connections and helping students see how individual ideas forms a
larger whole.
Concept maps are flexible. They can be made simple or detailed, linear,
3
branched, radiating or cross-linked.
 Linear concept maps are like flow charts that show how one
concept or event leads to another.
 Hierarchical concept maps represent information in a descending
order of importance. The key concept is on top, and subordinate concepts
fall below.

4.  Spider concept maps have a central or unifying theme in the center
of the map. Outwardly radiating sub-themes surround the main theme.
Spider concept maps are useful for brainstorming or at other times when
relationships between the themes need to be open ended.
 Cross-linked maps use a descriptive word or phrase and identify
the relationship with a labeled arrow.
4
Definition of a Concept Map
A Concept Map is a type of graphic organizer used to help students
organizer used to help students organize and represent knowledge of a subject.
Concepts maps begin with a main idea (or concept) and then branch out to show
how that main idea can be broken down into specific topics.

5. 5
Benefits of Concept Mapping
Concept Mapping sires several purposes for learners.
 Helping students brainstorm and generate new ideas.
 Encouraging students to discover new concepts and the propositions that
connect them.
 Allowing students to more clearly communicate ideas, thoughts and
information.
 Helping students integrate new concepts with older concepts.
 Enabling students to gain enhanced knowledge of any topic and evaluate
the information.
How to build a Concept Map
Concept maps are typically hierarchical, with the subordinate counts
stemming from the main concept or idea. This type of graphic organizer
however, always allows change and new concepts to be added. The
Rubber sheer analogy stated that concept positions on a map can
continuously change, while always maintaining the same relationship with
the other ideas on the map.
 Start with a main idea, or issue to focus on.
A helpful way to determine the context of your concept map is to choose a
focus question something that needs to be solved or a conclusion that
needs to be reached. Once a topic or question is decided on, that will help
with the hierarchical structure of the concept map.
 Then determine the key concepts.
Find the key concepts that connect and relate to your main idea and rank
them most general inclusive concepts come first then link to smaller more
specific concepts.

6.  Finish by connecting concepts creating linking phrases and words.
Once the basic links between the concepts are created, add cross – links,
which connect concepts in different areas of the map, to further illustrate
the relationships and strengthen students understanding and knowledge on
the topic.
6
Concept Maps in Education
When created correctly and thoroughly, concepts mapping is a powerful
way for students to reach high levels of cognitive performance. A concept map is
also not just a learning tool, but an ideal evaluation tool for educators measuring
the growth of and assessing student learning. As students create concept maps,
they reiterate ideas using their own words and help identify incorrect ideas and
concepts, educators are able to see what students do not understand providing an
accurate objective way to evaluate areas in which students do not get grasps
concepts fully.
Inspiration software , Webspiration classroom and Kidspiration
classroom service all contain diagram views that makes it easy for students to
create concept maps, students are able to add new concepts and links as they see
fit. Inspiration, inspiration and respiration classroom also come with a variety of
concept map examples, templates and lesson plans to show how concept
mapping and the use of other graphic organizer can easily be integrated into the
curriculum to enhance learning comprehension and writing skills.

7. SIMULATION
May topics in mathematics that have immediate utility value can be best
introduced using the technique of simulation that is enacting a real situation in
the class. Topics that have relation with commercial concern are an example.
The functioning of a co-operative society or bank can be cited as examples. First
the students may be taken to such institutions to observe the nature and
techniques of the various activities going on there. Notes may be taken. In order
to reinforce and to make the activity more familiar the working of such
institutions may be enacted in the class. The simulation should be carefully
arranged so as to make the insight as meaningful as possible.
For example, there is a school co-operative society. The working of the
society may be observed and the salient features of how it was organized and
what the activities taken up are noted. Then imagine that the learners are
planning to start a class co-operative society. The steps such as selling of shares
to pool the capital required election of various office bearers, nature of
transaction involved (together with the related mathematical skills) the style of
keeping records concerning the various aspects including the account book the
technique of preparing a balance sheet, calculation and dispersal of dividends to
the share holders etc may be simulated.
In the same way the activates in a Bank, which special reference to the
mathematical calculations involved (Such as deposits and withdrawals,
calculation of interests at various rates other money transaction giving loans etc.)
may be simulated in a realistic matter.
This will not only help in realizing the utility value of mathematics, but
also will give realistic insights into the related commercial mathematics. Further
the roles played in simulation will create interest among the learners.
7

8. 8
Definitions of Simulation
1. R. Wynn (1964): ‘Simulation is an accurate representation of
realistic situation.’
2. W.R. Fritz (1965): ‘Simulation may be considered as a
dynamic implementation of a model representing a physical or
a mathematical system.’
Simulation in Education
The International Dictionary of education defines the term as ‘teaching
technique used particularly in management education and training in which a
‘real life situation’ and values are simulated by ‘substitutes’ displaying similar
characteristics.’ It also means ‘Techniques in teacher education in which
students act out or role play teaching situations’ and values are simulated by
‘Substitutes’ displaying similar characteristics. It also means “Techniques in
teacher education in which students act out or role play teaching situations in an
attempt to make theory more practically oriented and realistic”
What is its purpose?
Simulations promote concept attainment through experiential practice.
Simulations are effective at helping students understand the nuances of a concept
or circumstance. Students are often more deeply involved in simulations than
other activities. Since they are living the activity the opportunity exists for
increased engagement.
Advantages
 Enjoyable, motivating activity.

9.  Element of reality of compatible with principles of constructivism.
 Enhances appreciation of the more subtle aspects of a concept / principle.
9
 Promotes critical thinking.
Disadvantages
 Preparation time
 Cost can be an issue
 Assessment is more complex than some traditional teaching methods.
How do I do it?
 Ensure that students understand the procedures before beginning. It
improves efficacy if the students can enjoy uninterrupted
participation. Frustration can arise with too many uncertainties’.
This will be counterproductive.
 Try to anticipate questions before they are asked. The pace of
some simulations is quick and the sense of reality is best
maintained with ready responses. Monitor student progress.
 Know what you wish to accomplish. Many simulations can have
more than one instructional goal. Developing a rubric for
evaluation is a worthwhile step. If appropriate, students should be
made aware of the specific outcomes expected of them.
Gradations
For effective teaching, concepts should be introduced step by step. This is
called Gradation. For students, to discover mathematical principles by their own,
it must be presented in a gradation way. The teaching should be proceeding from
simple to complex. This teaching technique is good for gradation.
Psychologically this is very important principle. If complex concepts introduce
from the beginning, that teaching will be ineffective. That will affect student's

10. confidence level and it makes concept attainment more difficult. Moreover they
can’t understand concepts on heuristic method by their own.
Let’s look at an example. Take the lesson addition. It can be arranged different
stages according to the difficulty level.
Stage 1: Primary addition facts – Sum that does not exceed 10 e.g:4+3=7
Stage 2: Primary additions fact – Sum that is greater than 10 e.g.: 7+5=12
Stage 3: Adding 3 or 4 numbers using primary addition facts e.g.:
5+4+5=14.
Stage 4: Adding secondary addition facts using primary addition facts.
E.g. – tens place value not changing. E.g. 5+2=7, likewise
10
15+2=17
Stage 5: Secondary addition facts – changing tens place value e.g. 7+5 =
12, likewise 17+5=22
Stage 6: Two two digit numbers addition – those with no remainders in
both positions. E.g. 22 + 33
Stage 7: Two two digit numbers addition. Where remainder comes only in
one position e.g. 45+37
Stage 8: Two two digit numbers – where zero will come as a result in ones
place value. E.g. 35+45
Stage 9: Two two digit numbers – where remainder comes also in tens
place value e.g. 75+48
Stage 10: Adding 3 or 4 one digit numbers e.g. 7+5+8+4
Stage 11: Including one digit & 2 digit numbers. E.g. 48+7+16+6

11. 11
Stage 12: Two three digit numbers.
Stage 13: Three two digit numbers etc.
By introducing stage wise addition facts mentioned above, that will
enable the addition principles which discover by the students their own and it
will makes the teaching effective. The main thing to be notices is that we should
proceed to the next stage only after the successful completion of each stage.
Maintaining the motivation by giving reinforcement through formative
evaluation. Understanding addition facts or any other mathematical facts is very
difficult for students without gradation. Moreover, because of the difficulty from
the vague concepts, students will feel afraid of mathematics.
In mathematics, all lessons we can teach like this. Gradation will make
the teaching meaningful. After the teaching is completed, each question should
give using gradation principles. That way start with simple problems then
difficult problems, this order has to be followed when giving problems.
Gradation is not including in subjects that also include in teaching
learning process. Like, concrete to abstract, simple to complex, empirical to
rational and known to unknown etc. These all gradation principles are using in
teaching learning process. A teacher should acquire a skill to start a class by
giving familiar facts and experiences for students. Piaget’s thoughts on cognitive
domain to make it firm through accommodation & assimilation in each steps,
and Gagne’s idea on chaining put more light into these gradation theory.
These all gradation principles are also known as maxims of teaching. The
maxims of teaching are very helpful in obtaining the active involvement and
participation of the learners in the teaching learning process. They make learning
effective, inspirational, interesting and meaningful. A good teacher should be
quite familiar with them.

12. 1. Proceed from the known to unknown.
The most natural and simple way of teaching a lesson is to proceed from
something that the students already know to those facts which they do not
know. What is already known to the students is of great use to the
students. This means that the teacher should arouse interest in a lesson by
putting questions on the subject matter already known to the pupils.
2. Proceed from simple to complex.
The simple task or topic must be taught first and the complex one can
follow later on. The word simple and complex are to be seen from the
point of view of the child and not that of an adult.
3. Proceed from easy to difficult.
We must graduate our lessons in order of case of understanding them.
Student's standard must be kept in view. This will help in sustaining the
interest of the students. There are many things which look easy to us but
are in fact difficult for children. The interest of the child has also to be
taken into account.
4. Proceed from concrete to the abstract.
A child’s imagination is greatly aided by a concrete material. “Things
first and words after” is the common saying. Rousseau said, “Things,
Things, Things, “Children in the beginning cannot think in abstractions.
Small children learn first from things which they can see and handle.
5. Proceed from particular to general.
Before giving Principles and rules, particular examples should be
presented. As a matter fact a study of particular facts should lead the
children themselves to frame general rules. The rules of arithmetic, of
12

13. grammar, of physical geography and almost of all sciences are based on
the principles of proceeding from particular instances to general rules.
6. Proceed from indefinite to definite.
Ideas of children in the initial states are indefinite, incoherent and very
vague. These ideas are to be made definite, clear, precise and systematic.
7. Proceed from empirical to rational.
Observation and experiences are the basis of empirical knowledge.
Rational knowledge implies a bit of abstraction and argumentative
approach. The general feeling is that the child first of all experiences
knowledge in his day to day life and after that the feels the rations bases.
8. Proceed from whole to parts.
Whole is more meaningful to the child than the parts of the whole.
13
9. From near to far.
A child learns well in the surroundings in which he resides. So he should
be first acquainted with his immediate environment.
10. From analysis to synthesis.
Analysis means breaking a problem into convenient parts and synthesis
means grouping these separated parts into one complete whole. A
complex problem can be made simple and easy by dividing it into units.

14. 14
References
en. wikipedia. Org / wiki / concept – map
www.inspiration .com / visual – learning / concept – mapping
Users. edte. utwente. nl / lanzing / cm-home. htm
olc. Spsd.sk.ca/De/PD/inst/r/strats/simul/index
Dark. Soman. (2010). ‘
Ganitha shastrabhodhanam’. Kerala: The state institute, of languages.
Dr. K. Soman, Dr. K. Sivarajan. (2008). ‘Mathematics Educations’. Calicut:
Calicut Universtiy.