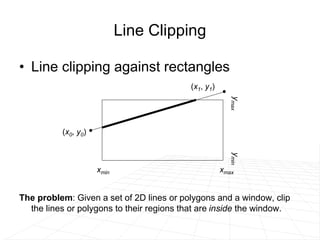
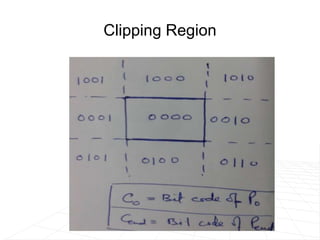
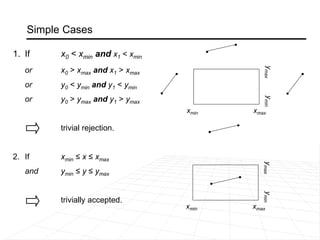
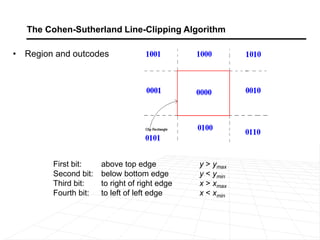
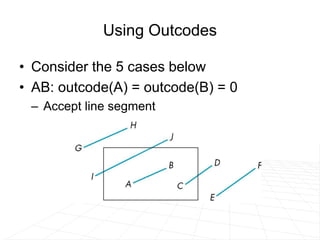
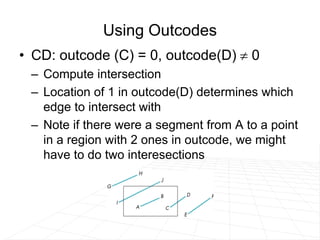
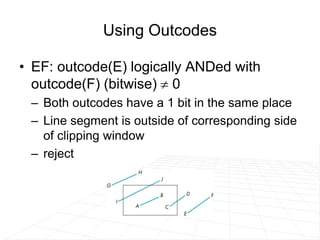
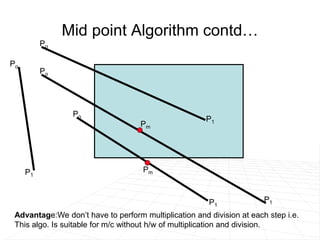
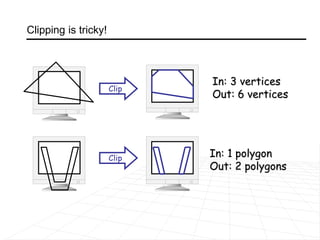
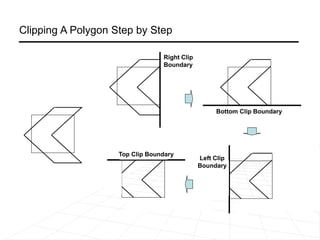
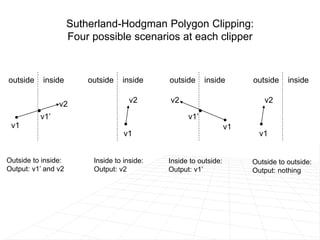
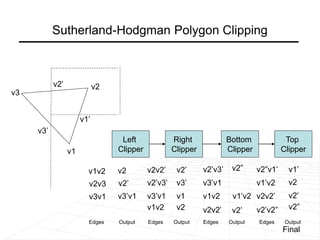
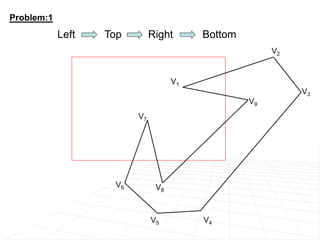
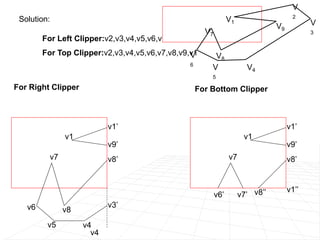
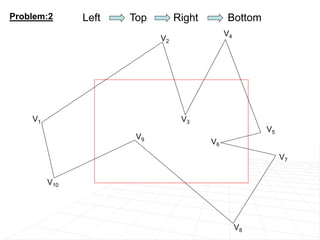
The document discusses different techniques for clipping lines and polygons to a viewing window or clipping region. It describes line clipping algorithms like Cohen-Sutherland that use outcodes to quickly reject lines outside the clipping region or clip lines intersecting the boundary. It also discusses the midpoint subdivision algorithm for line clipping. For polygon clipping, it explains the Sutherland-Hodgeman algorithm which clips polygons against each window edge one by one, dividing the polygon into smaller clipped polygons inside the viewing region.

1. Clipping
• Any procedure that identifies those portions of a
picture that are either inside or outside of a
specified region of space is referred to as a
clipping algorithm (or simply clipping)
• Everything outside the window is discarded
• Clipping algorithms can be applied in world co-
ordinates, so that only the contents of the
window interior are mapped to device co-
ordinates
• Alternately, the complete world co-ordinate
picture can be mapped first to device co-
ordinates, then clipped against the viewport

2. Clipping (contd..)
• World co-ordinate clipping removes those
primitives outside the window from further
consideration, thus eliminating the processing
necessary to transform those primitives to
device space.
• Viewport clipping ,can reduce calculations by
allowing concatenation of viewing and geometric
transformation matrices.
• But viewport clipping does require that the
transformation to device co-ordinates be
performed for all objects, including those outside
the window.

3. Line Clipping
• Line clipping against rectangles
The problem: Given a set of 2D lines or polygons and a window, clip
the lines or polygons to their regions that are inside the window.
(x1, y1)
xmin xmax
y
max
y
min
(x0, y0)

4. In: 3 vertices
Out: 6 vertices
Clip
Clip In: 1 polygon
Out: 2 polygons
Clipping is tricky!

5. 1. If x0 < xmin and x1 < xmin
or x0 > xmax and x1 > xmax
or y0 < ymin and y1 < ymin
or y0 > ymax and y1 > ymax
trivial rejection.
2. If xmin ≤ x ≤ xmax
and ymin ≤ y ≤ ymax
trivially accepted.
Simple Cases
xmin xmax
y
max
y
min
xmin xmax
y
max
y
min

6. • Region and outcodes
The Cohen-Sutherland Line-Clipping Algorithm
First bit: above top edge y > ymax
Second bit: below bottom edge y < ymin
Third bit: to right of right edge x > xmax
Fourth bit: to left of left edge x < xmin

7. • Checking for trivial acceptance or rejection using outcodes
1). Each endpoint of a line segment is assigned an outcode;
2). If both 4-bit codes are zero, the line can be trivially accepted;
3). A logical and is performed on both outcodes;
4). If the result is nonzero, the line can be trivially rejected.
The C-S Line-Clipping Algorithm (cont.)

8. Clipping Region

9. Algorithm
1.
2.
3.
4.

10. Advantages

11. DISADVANTAGES

12. Using Outcodes
• Consider the 5 cases below
• AB: outcode(A) = outcode(B) = 0
– Accept line segment

13. Using Outcodes
• CD: outcode (C) = 0, outcode(D)  0
– Compute intersection
– Location of 1 in outcode(D) determines which
edge to intersect with
– Note if there were a segment from A to a point
in a region with 2 ones in outcode, we might
have to do two interesections

14. Using Outcodes
• EF: outcode(E) logically ANDed with
outcode(F) (bitwise)  0
– Both outcodes have a 1 bit in the same place
– Line segment is outside of corresponding side
of clipping window
– reject

15. Using Outcodes
• GH and IJ: same outcodes, neither zero
but logical AND yields zero
• Shorten line segment by intersecting with
one of sides of window
• Compute outcode of intersection (new
endpoint of shortened line segment)
• Re-execute algorithm

16. Cohen-Sutherland Algorithm
• Now we can efficiently reject lines
completely to the left, right, top, or bottom
of the rectangle.
• If the line cannot be trivially rejected (what
cases?), the line is split in half at a clip
line.
• Not that about one half of the line can be
rejected trivially
• This method is efficient for large or small
windows.

17. Steps for Cohen-Sutherland Algorithm
1. End-points pairs are checked for trivial acceptance or rejection using
outcode;
2. If not trivially accepted or rejected, divide the line segment into two at
a clip edge;
3. Iteratively clipped by test trivial-acceptance or trivial-rejection, and
divided into two segments until completely inside or trivial-rejection.
A
B
C
D
E
F
G
H
I
1001
0001
0101 0100
0000
1000 1010
0010
0110

18. Calculation of Intersection Points
• Intersection points with a clipping
boundary can be calculated using slope-
intercept form of the line equation.
• For a line with end points co-
ordinates(x0,y0) and (x1,y1).
• The y co-ordinate of the intersection point
with a vertical boundary can be obtained
with the calculation
y= y1 +m ( x – x1)

19. • The slope of the line is calculated as
• Similarily, if we are looking for the intersection of
horizontal boundary the x co-ordinate can be calculated
as
• Now find the intersection point;
• y = y0 + slope * (x - x0),
• x = x0 + (1/slope)* (y - y0)
• With y is set to either Ymin or Ymax
• Where x value is either set to Xmin or Xmax`
y1-y0 / x1-x0

20. Mid point Algorithm
• We can subdivide the line to avoid direct
computation of the line’s point of
intersection with the edges of screen
• Midpoint subdivision algorithm clips the
line by finding the end points of its visible
segment. The goal of this process is to
find the visible point on any line segment.

21. • The steps are as follows:-
• If a line P0P1 is given.
• We test P1 is visible if so ,it is the visible point
from P0 and process is complete. If it is invisible
then continue
• We check whether P0P1 can be rejected i.e.
entirely off the screen if so process is complete
& no output is generated, otherwise continue.
• Divide P0P1 at its midpoint Pm if the segment
PmP1 can be rejected we have over estimated
and we repeat from step2 using line segment
P0Pm,otherwise we repeat step2 using line
segment PmP1
Mid point Algorithm contd…

22. Po
Po
Po
Po
Pm
P1
P1
P1
P1
Pm
Mid point Algorithm contd…
Advantage:We don’t have to perform multiplication and division at each step i.e.
This algo. Is suitable for m/c without h/w of multiplication and division.

23. Polygon Clipping
• A polygon boundary processed with a line
clipping displayed as a series of unconnected
line segments but we want to display
bounded area after clipping.
• The output of a polygon clipper should be a
sequence of vertices that defines the clipped
polygon boundaries

24. Polygon Clipping
• Sutherland-Hodgeman algorithm (A divide-and-conquer
strategy)
• Polygons can be clipped against each edge of the
window one at a time. Edge intersections, if any,
are easy to find since the X or Y coordinates are
already known.
• Vertices which are kept after clipping against one
window edge are saved for clipping against the
remaining edges.
• Note that the number of vertices usually changes
and will often increases.

25. Top Clip Boundary
Clipping A Polygon Step by Step
Right Clip
Boundary
Bottom Clip Boundary
Left Clip
Boundary

26. Sutherland-Hodgeman Algorithm
Given a polygon with n vertices, v1, v2,…, vn, the algorithm clips the
polygon against a single, infinite clip edge and outputs another series
of vertices defining the clipped polygon. In the next pass, the partially
clipped polygon is then clipped against the second clip edge, and so
on.
Let’s considering the polygon edge from vertex vi to vertex vi+1.
Assume that start point vi has been dealt with in the previous iteration,
four cases will appear.
This algorithm requires storage for only two pairs of co-ordinates for
each clipping edge

27. Sutherland-Hodgman Polygon Clipping
• Input each edge (vertex pair) successively.
• Output is a new list of vertices.
• Each edge goes through 4 clippers.
• The rule for each edge for each clipper is:
– If first input vertex is outside, and second is inside,
output the intersection and the second vertex
– If first both input vertices are inside, then just output
second vertex
– If first input vertex is inside, and second is outside,
output is the intersection
– If both vertices are outside, output is nothing

28. Sutherland-Hodgman Polygon Clipping:
Four possible scenarios at each clipper
outside inside
v1
v1’
v2
outside inside
v1
v2
outside inside
v1
v1’
v2
outside inside
v1
v2
Outside to inside:
Output: v1’ and v2
Inside to inside:
Output: v2
Inside to outside:
Output: v1’
Outside to outside:
Output: nothing

29. Sutherland-Hodgman Polygon Clipping
v2
v1
v3
Right
Clipper
Bottom
Clipper
Top
Clipper
Left
Clipper
v1v2
v2v3
v3v1
v1’
v2
v2’
v2’
v3’v1
v2v2’
v2’v3’
v3’v1
v1v2
v2’
v3’
v1
v2 v2v2’
v2’v3’
v3’v1
v1v2
v3’
v2”
v1’v2
v2’ v2’v2”
v2”v1’
v1’v2
v2v2’
v1’
v2
v2’
v2”
Edges Output Edges Output Edges Output Edges Output
Final

30. V1
V2
V3
V4
V9
V7
V6
V5
Problem:1
V8
Left Top Right Bottom

31. For Left Clipper:v2,v3,v4,v5,v6,v7,v8,v9,v1
For Top Clipper:v2,v3,v4,v5,v6,v7,v8,v9,v1
For Right Clipper
v1’
v1
v9’
v8’
v8
v7
v6
v5 v4
v3’
v4
v1’
v1
v9’
v8’
v8’’
v7
v6’
v1’’
v7’
For Bottom Clipper
Solution: V1
V
2
V
3
V4
V9
V7
V
6
V
5
V8

32. Problem:2
V1
V2
V3
V4
V5
V6
V7
V8
V9
V10
Left Top Right Bottom

33. Ground Rules for graphics system design:
The main difficulty in constructing such a package is to give adequate
consideration to many issues that effect the usefulness of the package
some of the issues are:
Simplicity: Features that are too complex for application programmer to
understand will not be used . It is often difficult for the graphics package
designer to detect potentially difficult aspects of the design. These aspects
become more obvious when the user’s manual is written.
One way to avoid these difficult features is to write the user’s manual
before implementing the system. .
Consistency: A consistent graphics system is one that behaves in a
predictable manner .Function names ,calling sequences , error handling
and co-ordinate systems all should follow simple and consistent patterns
without exceptions.
So, application programmer is then able to build up a conceptual model of
how the package functions

34. Completeness: there should be no irritating omissions in the set of
functions provided by the system, missing functions will have to be supplied by
application programmer , who may not have the necessary access to the
computer’s resources to be able to write them.
Completeness doesn’t imply comprehensiveness i.e. the system need not
provide every graphics facility (imaginable). The system designer must try to
design a small set of functions that can conveniently handle a wide range of
application.
Robustness: Application programmers are capable of extraordinary misuse
of graphics systems either through misunderstanding or through the
mischievous enjoyment of trying everything once. The system should accept
such treatment with minimum complaint. Trivial errors of omission or repetition
should be corrected without comment from the system.
When the programmer does something seriously wrong ,the system should
report the error in the most helpful manner. Only in extreme circumstances
should errors cause termination of execution (otherwise it will cause user to
lose valuable result)

35. Performance: Graphics system performance is often limited by
factors such as Operating System response, display characteristics,
system beyond the system design control.
Economy: It is always frustrating to write an application program
that is too bulky and too expensive to use.
Graphics system should be small and economical so that adding
graphics to an existing application program can always be considered

36. Functional Domain:
Anyone who designs a graphics package must include two points:
 Graphics package design must not be influenced by h/w features or
by highly specialized application requirements.
 Functions in the graphics package can be separated into sets. Each
set is concerned with a particular kind of task. It is then possible to
address the issue of completeness i.e one set at a time
The graphics package should provide the following two functional sets:
Graphics Primitives:
Graphics Primitives are the functions that we use to specify or display
the actual lines and text strings, circular arcs and other simple graphical
items
e.g: line(), lineto(), circle(), arc(), rectangle()
Windowing Functions:
These allow the programmer to choose co-ordinate system for picture
definition and to define the boundary of the visual portion
e.g: setviewport()

37. Other function sets include segmentation function to permit easier modification
Of the picture 2D-transformation function for rotation, translation, scaling
And I/P functions that allow user to give commands with the help of keyboard
or graphical I/P device.
In addition to these functions there are a number of miscellaneous utility
functions such as initgraph(), getmaxx(),getmaxy(), detectgraph(), clearscreen().
The initial phase of the system design involves certain number of these sets to
form functional domain of system. We then attempt to achieve the
comprehensive collection with in each set.