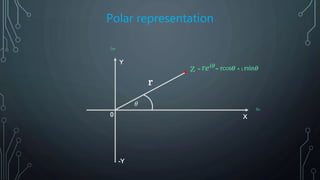
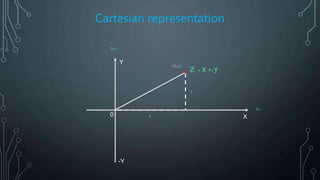
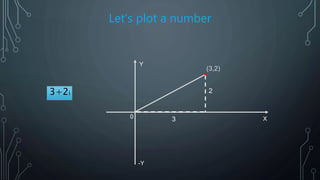
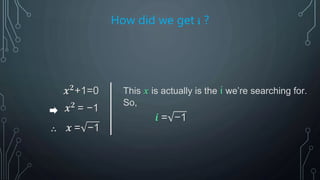The document explains complex numbers as a combination of real and imaginary numbers, illustrated through historical milestones and graphical representations such as Argand diagrams. It discusses key developments by figures like Heron, Cardano, Descartes, and Euler, and highlights applications in various fields including electrical engineering, signal analysis, and quantum mechanics. The document emphasizes both the mathematical foundations and practical uses of complex numbers.

1. Representation of Complex Number
Presentation on

2. What is complex number?
Complex number is a union of Real numbers and
Imaginary numbers.

3. Venn Diagram
Imaginary Number
0 + yi
Real Number
x + 0i
Complex Number
x + yi

4. Historical events
o In 50 A.D. Heron of Alexandria studied the volume of an
impossible section of a pyramid. He calculated the value
as 𝟖𝟏 − 𝟏𝟏𝟒 which was impractical in the then period.

5. Historical events
o In 1545, Girolamo Cardano solved the equation x(10-x) =
40, finding the answer to be 5 ± −15 . He used to dislike
imaginary number and called them as “mental tortures”.

6. Historical events
o In 1637, Rene Descartes came up with the standard form
for complex numbers which is a + bi. However, he didn’t
like complex numbers either.

7. Historical events
o In 1777, Euler made the symbol i stands for √-1, which
made it a little easier to understand complex number.

8. How did we get i ?
𝒙 𝟐
+1=0
𝒙 𝟐
= −1
∴ 𝒙 = −1
This 𝒙 is actually is the i we’re searching for.
So,
𝒊 = −1

9. Graphical representation
Graphical Representation
Polar form Cartesian form
The graphical representation or pictorial
representation of complex number is implemented in
Argand diagram.

10. Polar representation
Im
Re
X
Y
0
-Y
𝜃
r
= r𝒆𝒊𝜽= rcos𝜽 + i rsin𝜽Z

11. Cartesian representation
Im
Re
X
Y
0
-Y
= x +i y
(x,y)
x
y
Z

12. Let’s plot a number
X
Y
0
-Y
3+2i
(3,2)
3
2

13. Applications
o To find impedance of an RLC circuit:
𝑍 = 𝑅 + 𝑗 𝑋
V

14. Applications
o To find AC voltage:
𝑉 = 𝑉0 𝑒 𝑗𝜔𝑡
V

15. Applications
o To do signal analysis:
Image After FFT
𝑋 𝑘 = ∑𝑥 𝑛 𝑒−2𝜋𝑖𝑘𝑛/𝑁

16. Applications
o To do signal sampling:
E-mu Emax
 This has a button called “Transform multiply”
 This is a fancy name of convolution
 Convolution is performed using DFT method

17. Applications
Other fields of application in a nut shell:
 Relativity
 Fluid dynamics
 Quantum mechanics
 Improper integrals
 Control theory

18. Any Query?

19. Thanks!