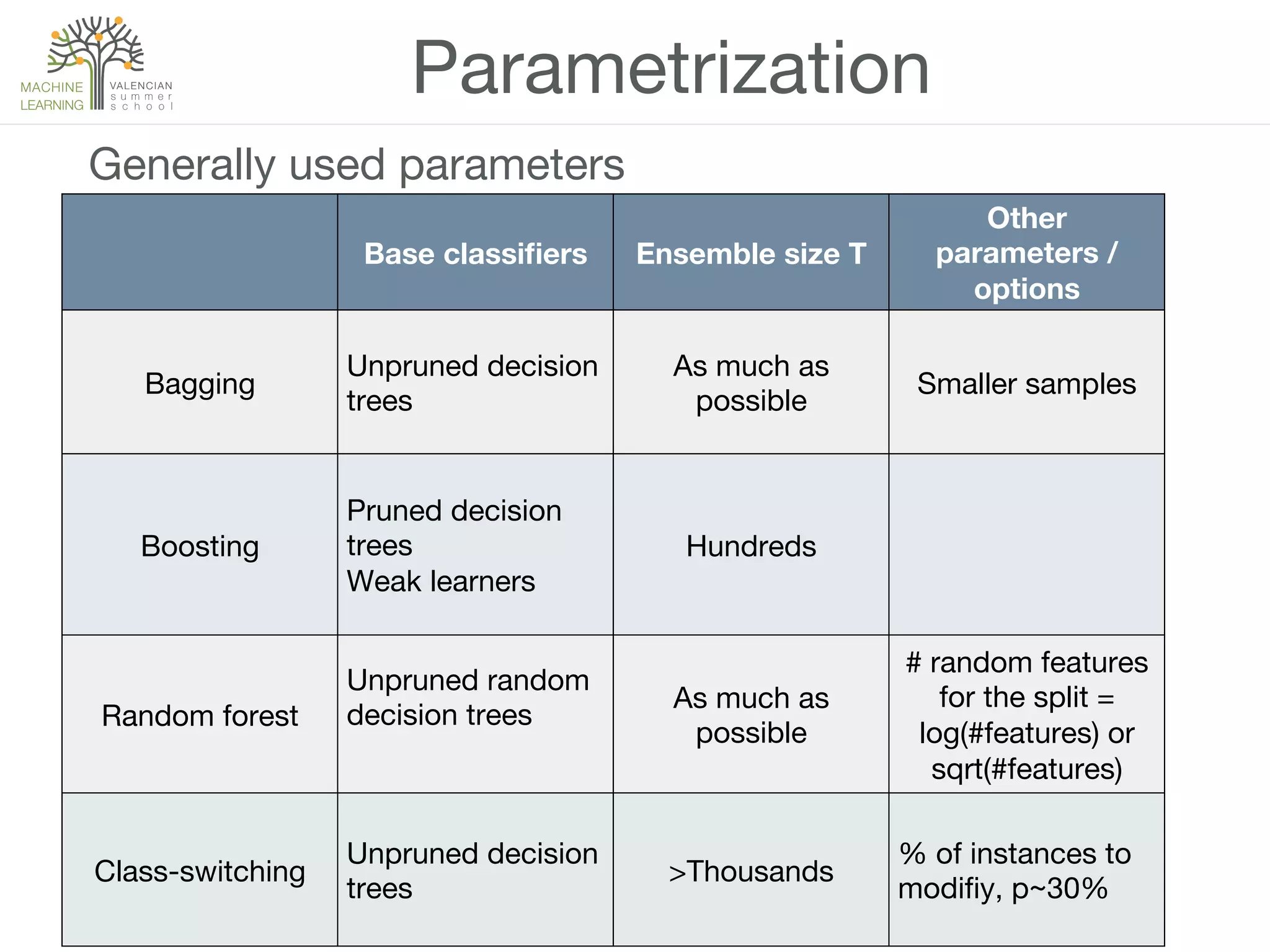
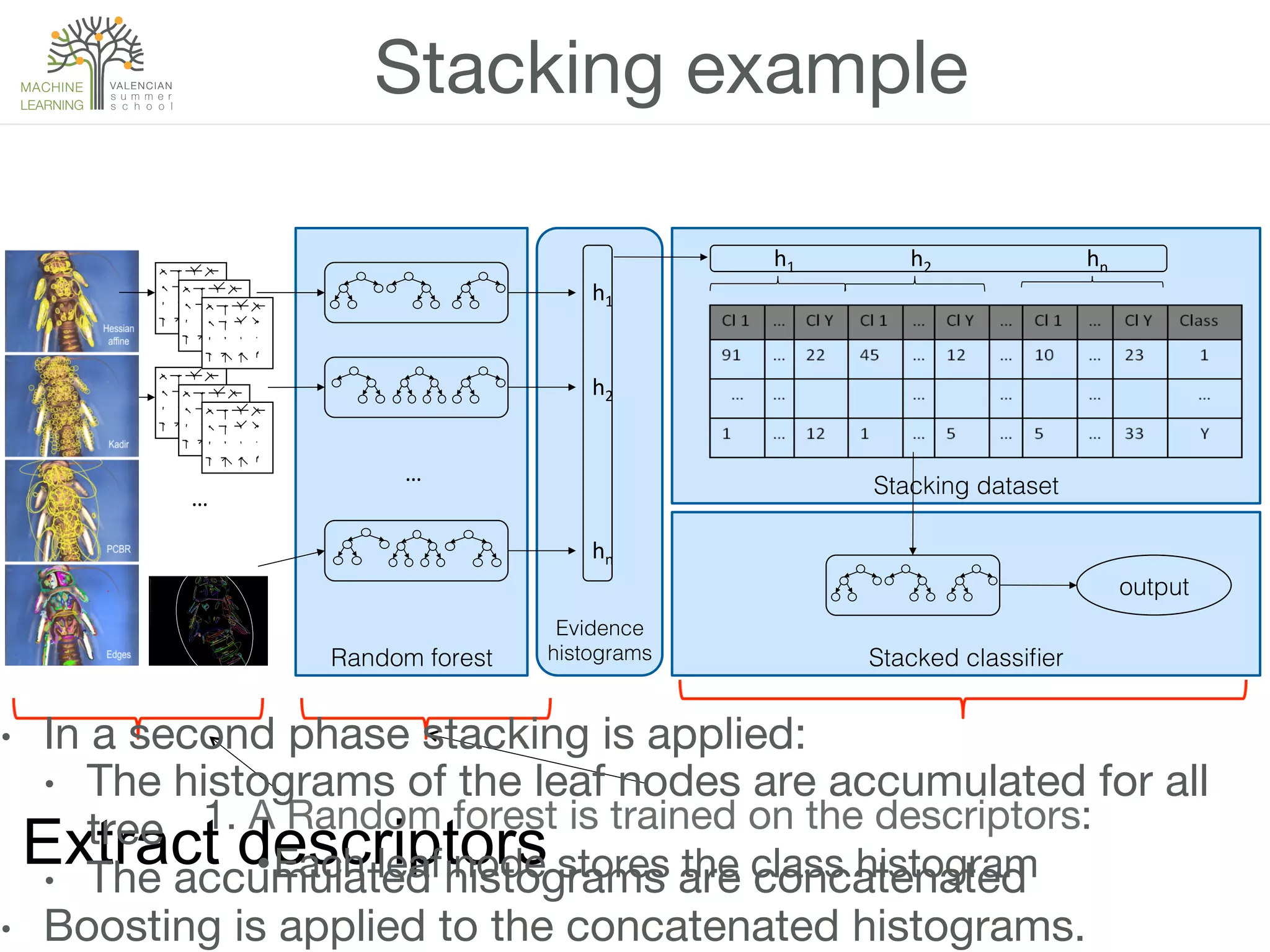
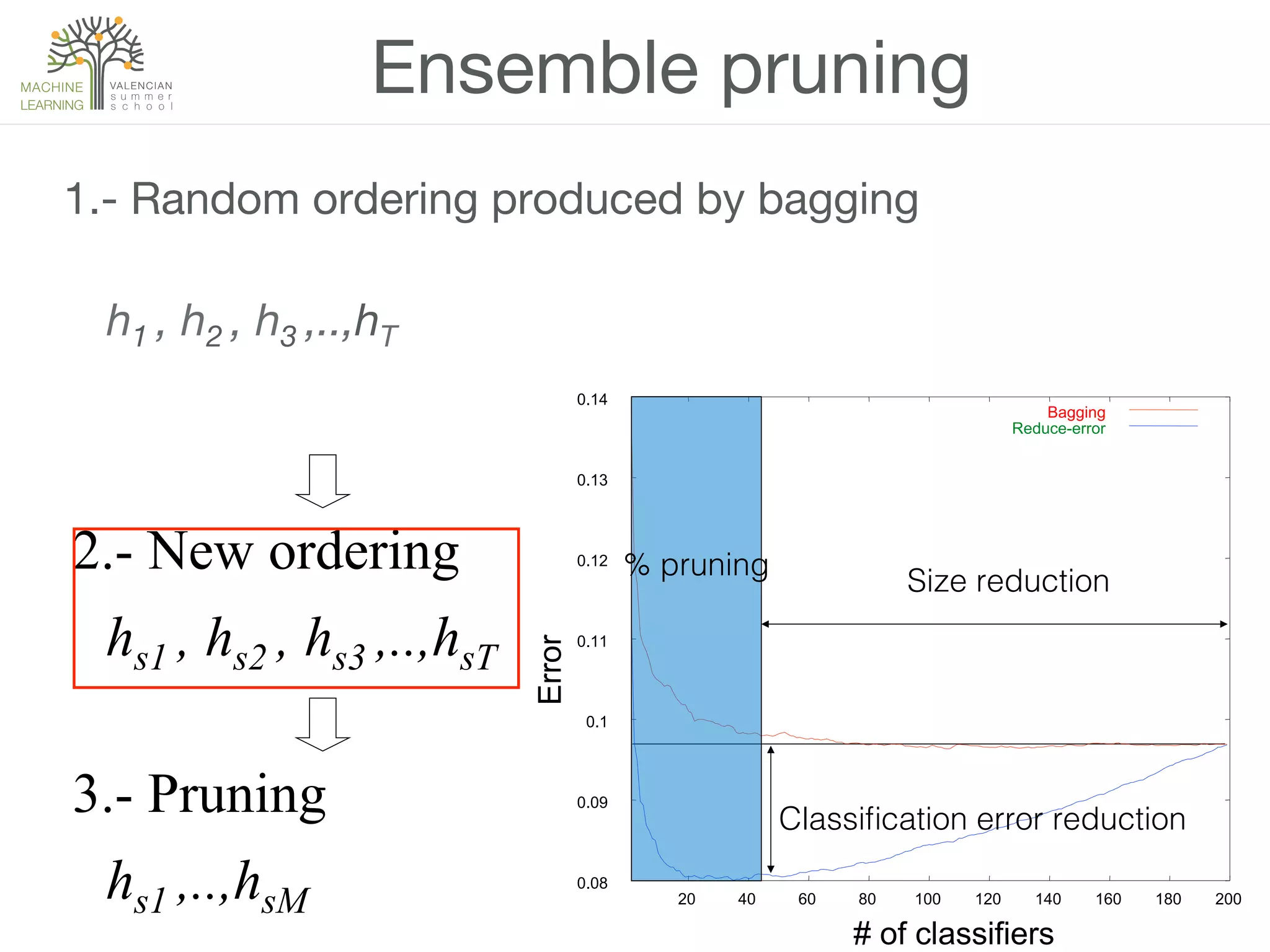
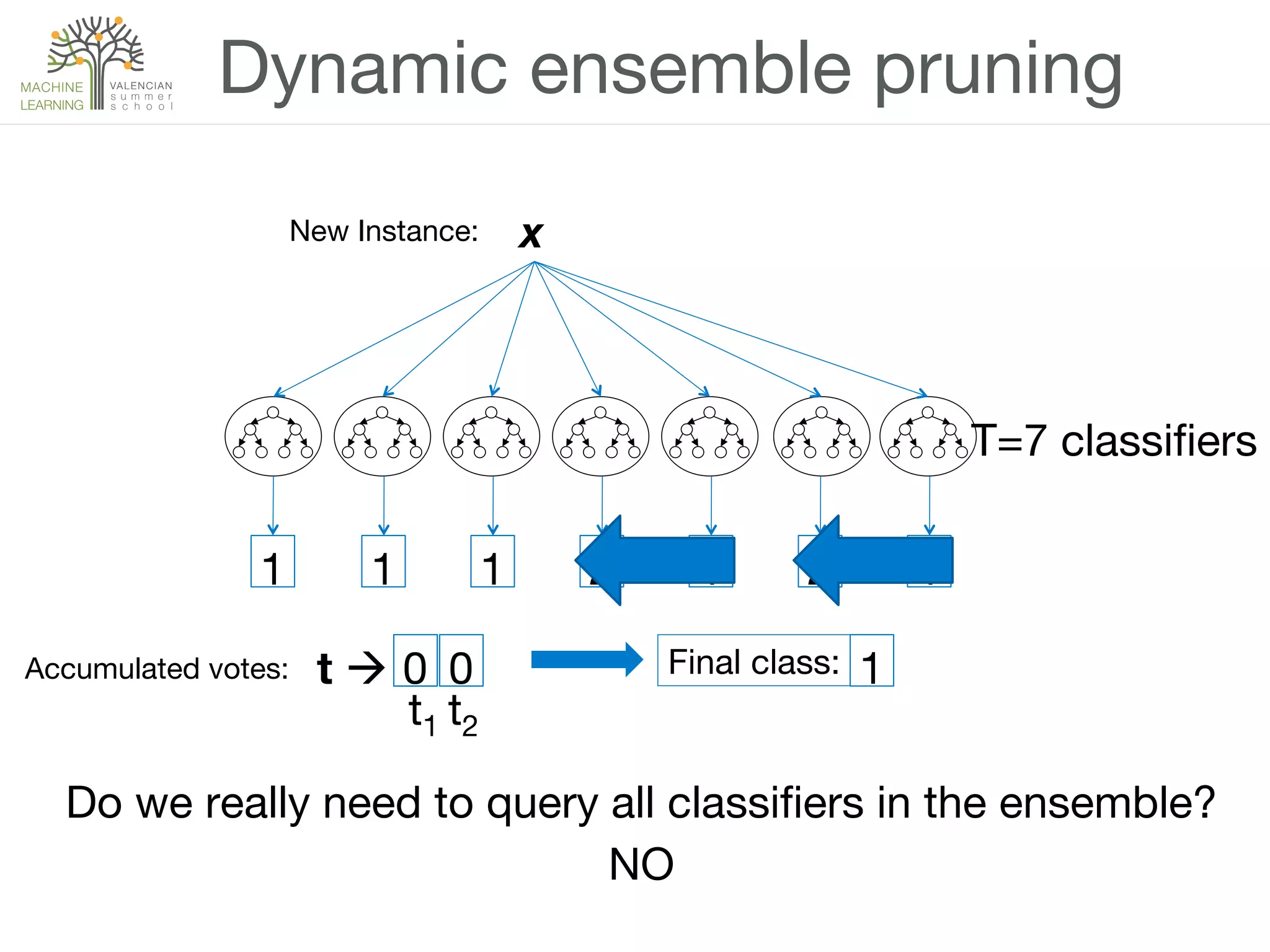
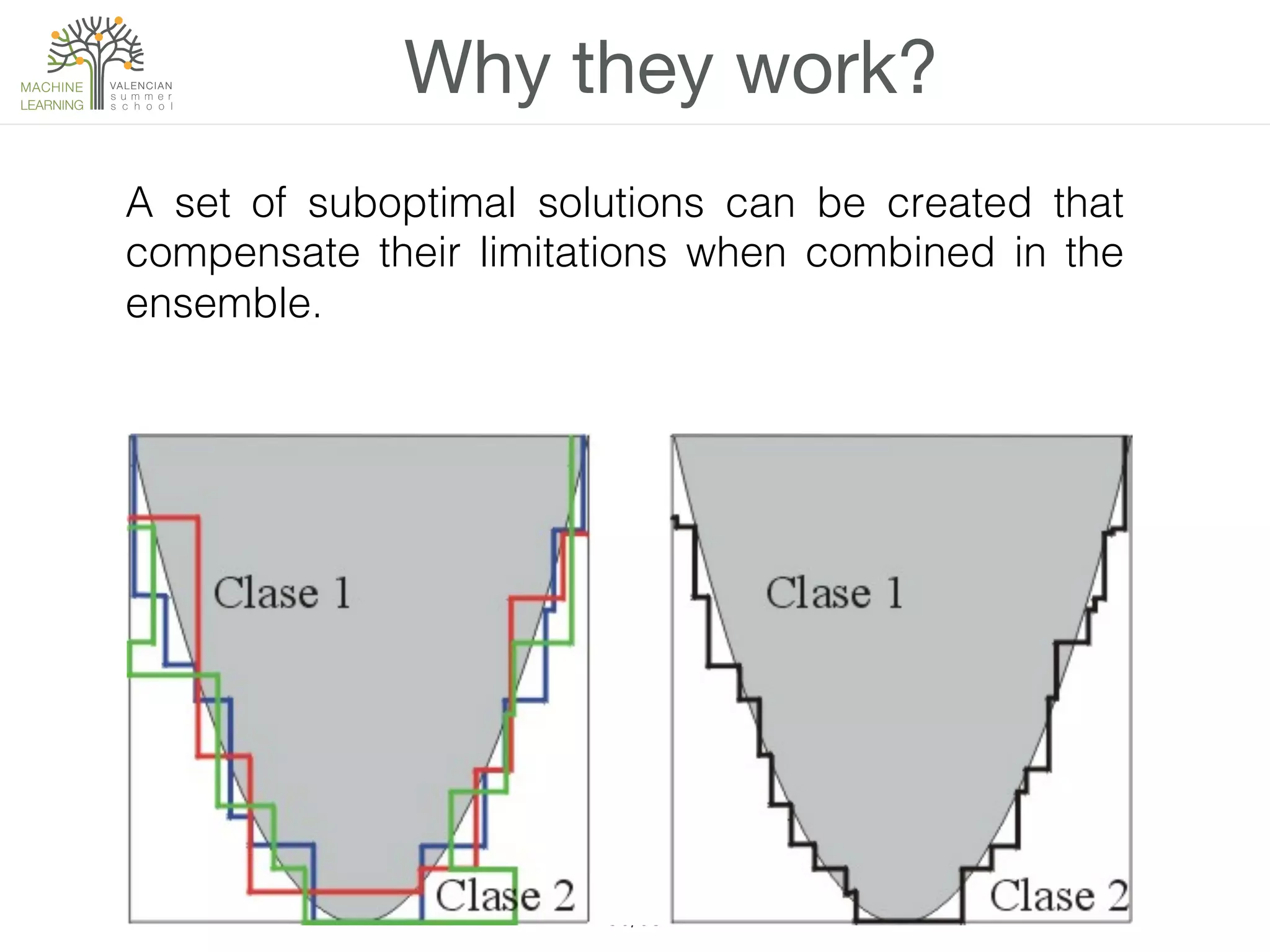
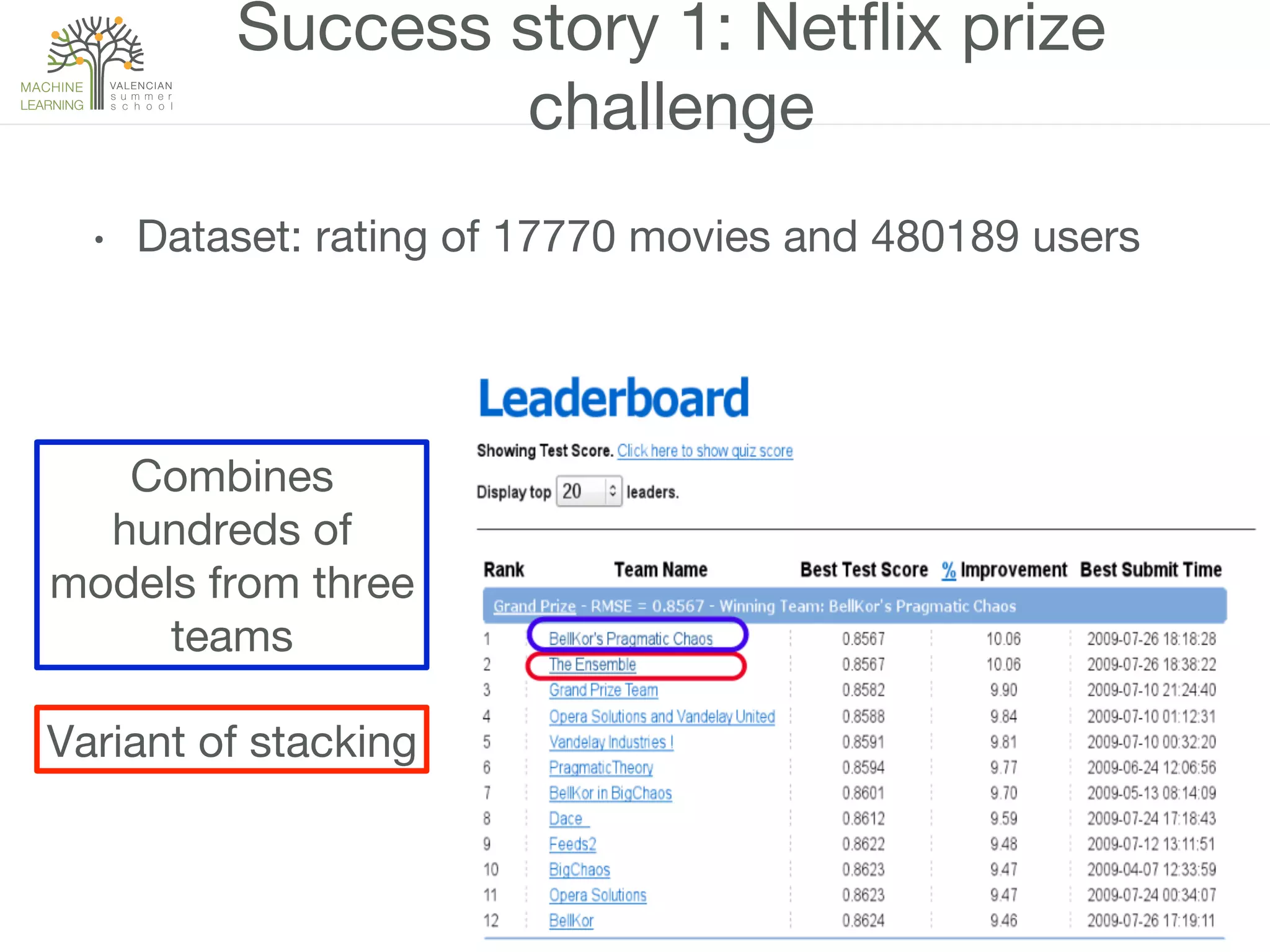
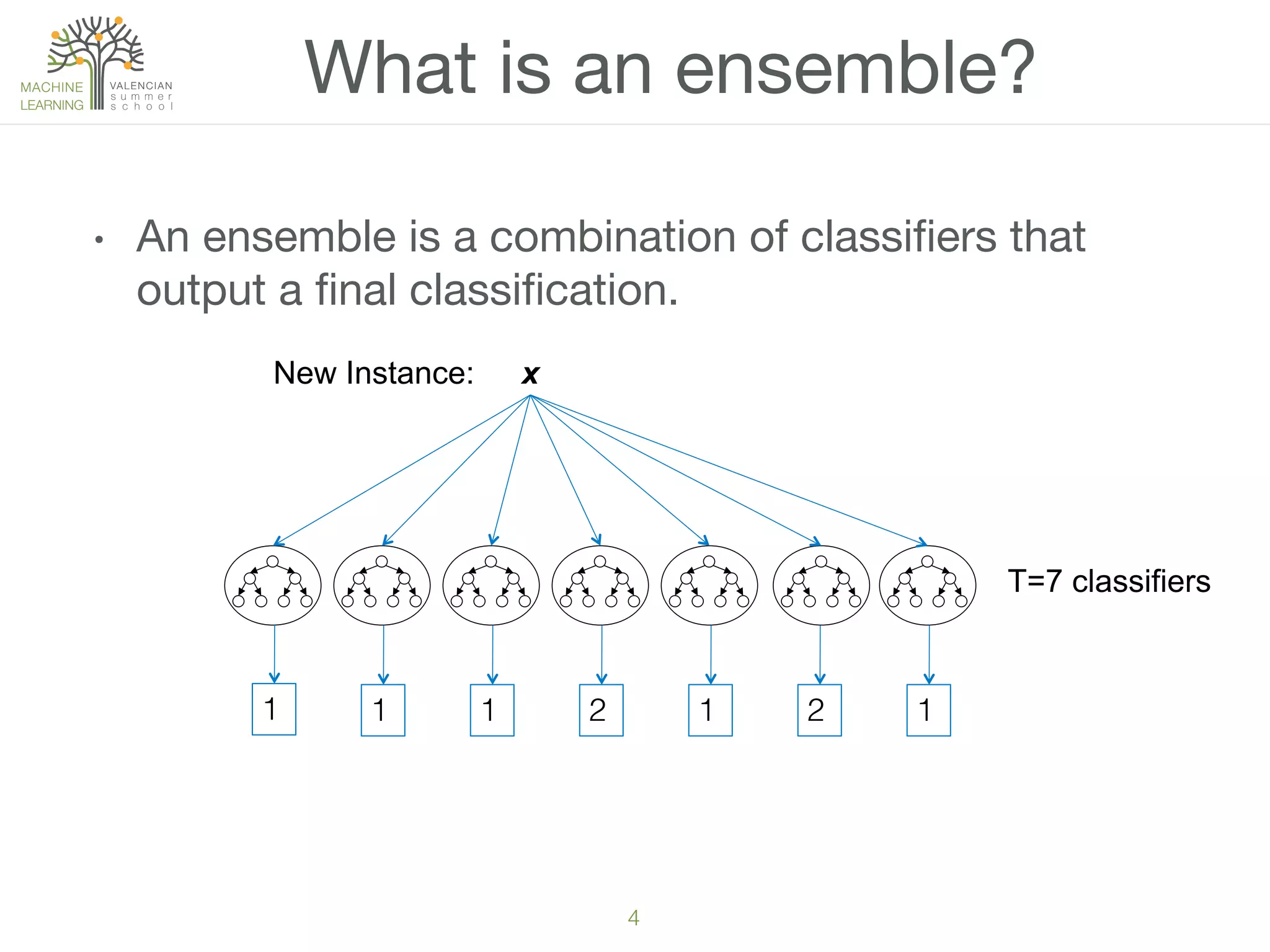
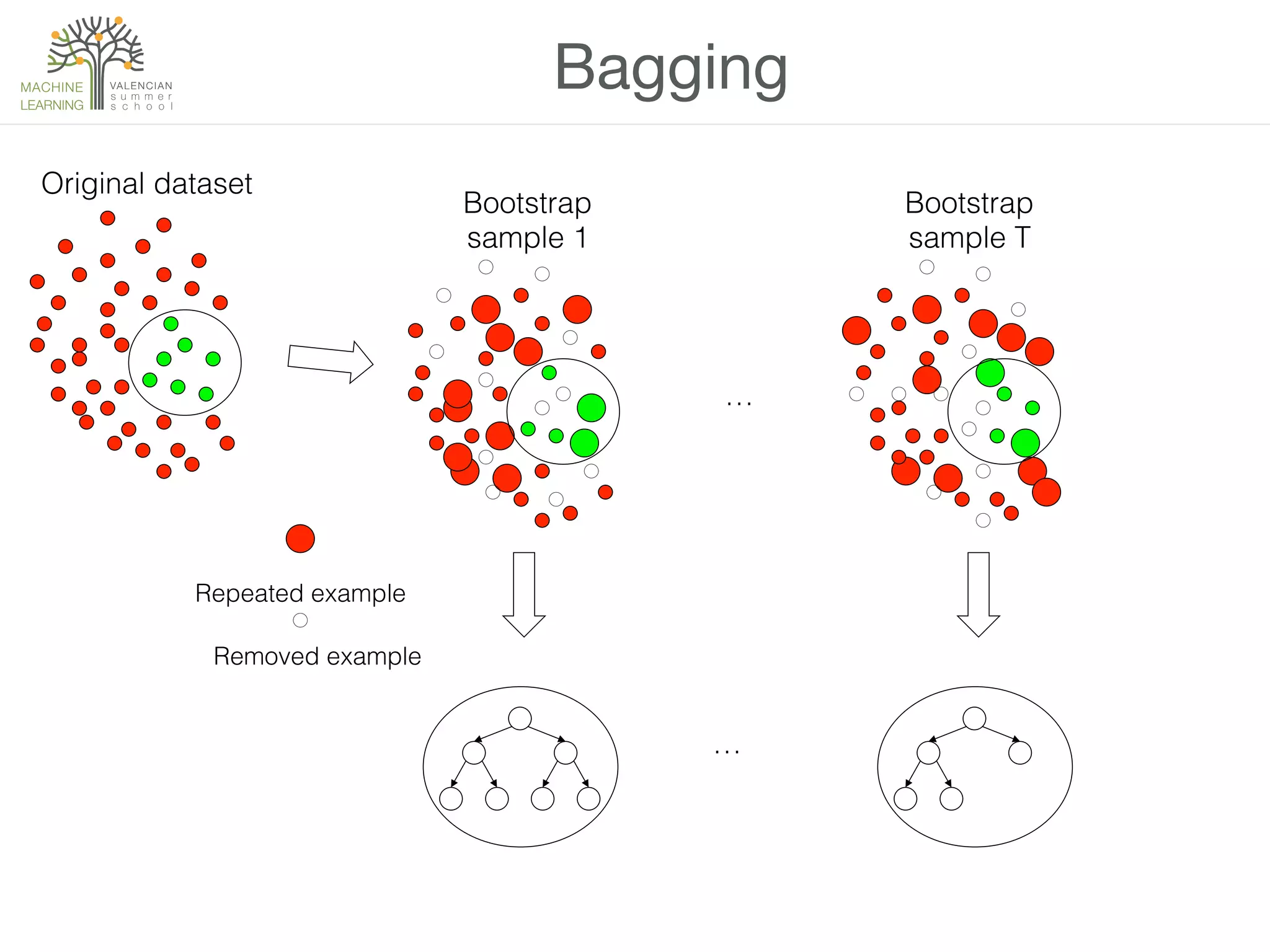
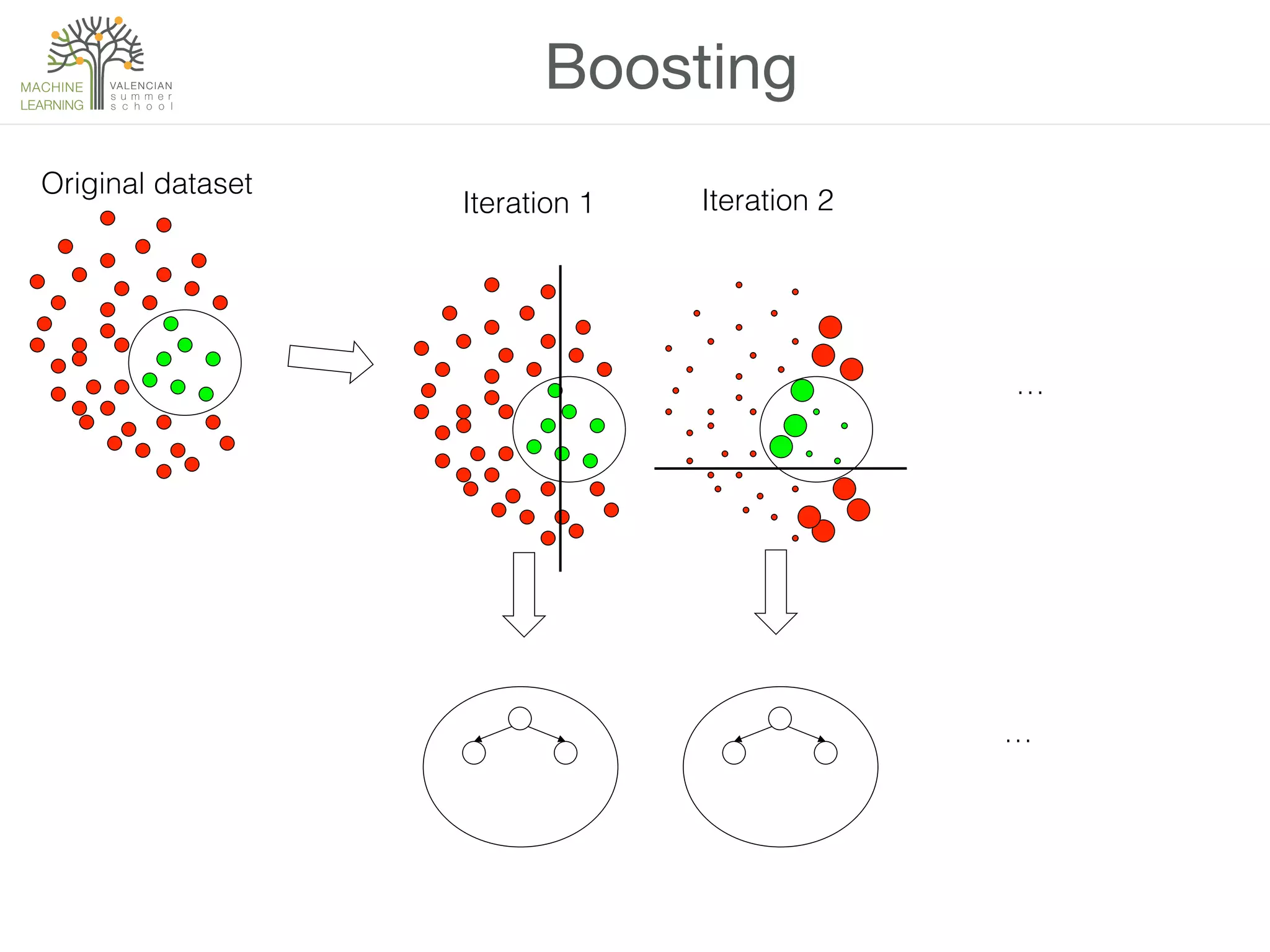
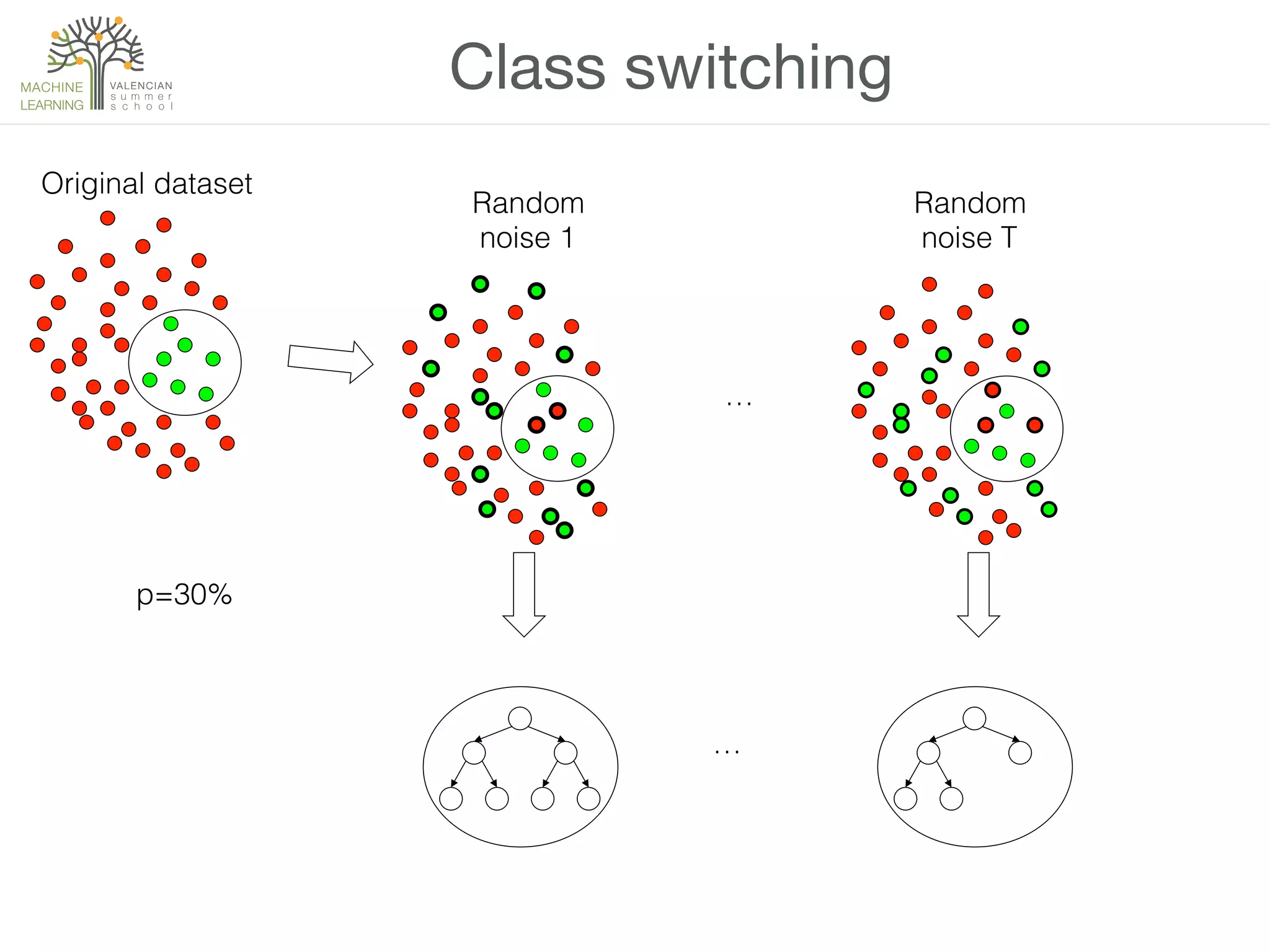
The document discusses ensemble methods in machine learning, which involve combining multiple classifiers to enhance performance. It outlines various techniques for building ensembles, such as bagging, boosting, and random forests, and explains the principles behind their effectiveness, including the Condorcet Jury Theorem. The text also highlights success stories from competitions like the Netflix Prize and KDD Cup, showcasing the practical application of these strategies.

1. Ensembles
Gonzalo Martínez Muñoz
Universidad Autónoma de Madrid

2. 2!
• What is an ensemble? How to build them?
• Bagging, Boosting, Random forests, class-
switching
• Combiners
• Stacking
• Other techniques
• Why they work? Success stories
Outline

3. • The combination of opinions is rooted
in the culture of humans
• Formalized with the Condorcet Jury
Theorem:
Given a jury of voters and assuming
independent errors. If the probability of
each single person in the jury of being
correct is above 50% then the
probability of the jury of being correct
tends to 100% as the number persons
increase
Condorcet Jury theorem
Nicolas de Condorcet (1743-1794),!
French mathematician!

4. 4!
• An ensemble is a combination of classifiers that
output a final classification.
What is an ensemble?
New Instance: x
1! 1! 2! 1! 2! 1!
T=7 classifiers
1!

5. General idea
• Generate many classifiers and combine them to get
a final classification
• They perform very good. In general better than any
of the single learners they are composed of
• The classifiers should be different from one another
• It is important to generate diverse classifiers from
the available data
5/63!

6. How to build them?
• There are several techniques to build diverse base
learners in an ensemble:
• Use modified versions of the training set to train
the base learners
• Introduce changes in the learning algorithms
• These strategies can also be used in combination.
• Generally the greater the randomization the better
are the results

7. How to build them?
• Modifications of the training set can be generated by
• Resampling the dataset. By bootstrap sampling (e.g.
bagging), weighted sampling (e.g. boosting).
• Altering the attributes: The base learners are trained
using different feature subsets (e.g Random
subspaces)
• Altering the class labels: Grouping classes into two
new class values at random (e.g. ECOC) or modifying
at random the class labels (e.g. Class-switching)

8. How to build them?
• Randomizing the learning algorithms
• Introducing certain randomness into the learning
algorithms, so that two consecutive executions of
the algorithm would output different classifiers
• Running the base learner with different
architectures, paremeters, etc.

9. Bagging
Input:
Dataset L
Ensemble size T
1.for t=1 to T:
2. sample = BootstrapSample(L)
3. ht = TrainClassifier(sample)
( )( )⎟
⎠
⎞
⎜
⎝
⎛
== ∑=
T
t
t
j
jhIH
1
argmax)( xx
Bootstrap
Aggregation
+Output:

10. Bagging
Original dataset!
Bootstrap !
sample 1!
!
Repeated example!!
Removed example!
…!
…!
Bootstrap !
sample T!

11. Considerations about bagging
• Uses 63,2% of the training data on average to build
each classifier.
• It is very robust against label noise.
• In general, it improves the error of the single
learner.
• Easily parallelizable

12. Boosting
Input:
Dataset L
Ensemble size T
1.Assign example weights to 1/N
2.for t=1 to T:
3. ht = BuildClassifier(L, pesos)
4. et = WeightedError(L, pesos)
5. if et==0 or et ≥ 0.5 break
6. Multiply incorrectly classified
instances weights ht by et/
(1-et)
7. Normalize weights

13. Boosting
Original dataset!
Iteration 1!
…!
…!
Iteration 2!

14. Considerations about boosting
• Obtains very good generalization error on average
• It is not robust against class label noise
• It can increment the error of the base classifier
• Cannot be easily implemented in parallel

15. Random forest
• Breiman defined a Random forest as an ensemble
that:
• Has decision trees as its base learner
• Introduces some randomness in the learning
process.
• Under this definition bagging of decision trees is a
random forest and in fact it is. However…

16. Random forest
• In practice, it is often considered an ensemble that:
• Each tree is generated, as in bagging, using bootstrap
samples
• The tree is a special tree that each split is computed
using:
• A random subset of the features
• The best split within this subset is then selected
• Unpruned trees are used

17. Considerations about random
forests
• Its performance is better than boosting in most
cases
• It is robust to noise (does not overfit)
• Random forest introduces an additional
randomization mechanism with respect to bagging
• Easily parallelizable
• Random trees are very fast to train

18. Class switching
• Class switching is an ensemble method in which
diversity is obtained by using different versions of
the training data polluted with class label noise.
• Specifically, to train each base learner, the class
label of each training point is changed to a different
class label with probability p.

19. Class switching
Original dataset!
Random!
noise 1!
…!
…!
Random!
noise T!
p=30%!

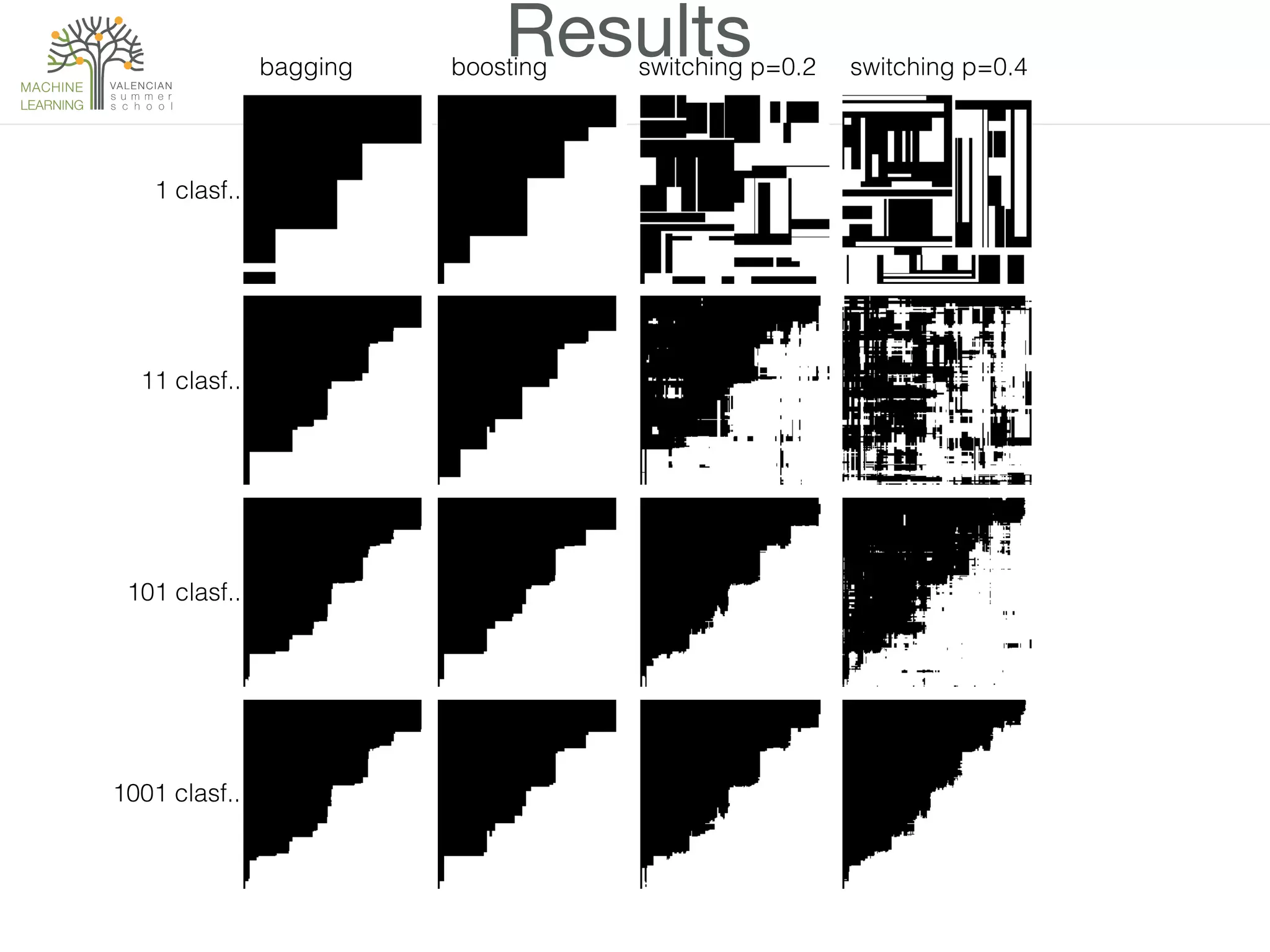
20. Example
• 2D example
• Boundary is x1=x2
• x1~U[0, 1] x2~U[0, 1]
• Not an easy task for a normal decision tree
• Let’s try bagging, boosting and class-switching with
p=0.2 y p=0.4
x1
x2
Clase 1
Clase 2
1
1

21. bagging! boosting! switching p=0.2! switching p=0.4!
1 clasf..!
11 clasf..!
101 clasf..!
1001 clasf..!
Results

22. 22!
Parametrization
Base classifiers
Ensemble size T
Other
parameters /
options
Bagging
Unpruned decision
trees
As much as
possible
Smaller samples
Boosting
Pruned decision
trees
Weak learners
Hundreds
Random forest
Unpruned random
decision trees
As much as
possible
# random features
for the split =
log(#features) or
sqrt(#features)
Class-switching
Unpruned decision
trees
>Thousands
% of instances to
modifiy, p~30%
Generally used parameters !

23. Combiners
• The combination techniques can be divided into two
groups:
• Voting strategies: The ensemble prediction is the class
label that is predicted most often by the base learners.
Could be weighted
• Non voting strategies: Some operations such as
maximum, minimum, product, median and mean can
be employed on the confidence levels that are the
output of the individual base learners.
• There is no winner strategy among the different
combination techniques. Depends on many factors

24. Stacking
• In stacking the combination phase included in the
learning process.
• First the base learners are trained on some version of
the original training set
• After that, the predictions of the base learners are used
as new feature vectors to train a second level learner
(meta-learner).
• The key point in this strategy is to improve the guesses
that are made by the base learners, by generalizing
these guesses using a meta learner.

25. Evidence!
histograms! Stacked classifier!
Stacking dataset!
Random forest!
…
…
h1
h2
hn
h1
h2
hn
output!
Stacking example
Extract descriptors
1. A Random forest is trained on the descriptors:
• Each leaf node stores the class histogram
• In a second phase stacking is applied:
• The histograms of the leaf nodes are accumulated for all
tree
• The accumulated histograms are concatenated
• Boosting is applied to the concatenated histograms.

26. 1.- Random ordering produced by bagging
h1 , h2 , h3 ,..,hT
0.08!
0.09!
0.1!
0.11!
0.12!
0.13!
0.14!
20! 40! 60! 80! 100! 120! 140! 160! 180! 200!
Error!
# of classifiers!
Bagging!Reduce-error!CART!
2.- New ordering
hs1 , hs2 , hs3 ,..,hsT
% pruning!
!
!
!
3.- Pruning
hs1 ,..,hsM
Size reduction!
Classification error reduction!
Ensemble pruning

27. Accumulated votes:
2
1
5
4
3
2
1
Dynamic ensemble pruning
New Instance:
x
1
t à
1
1
2
1
2
1
T=7 classifiers
0
0
Final class:
1
Do we really need to query all classifiers in the ensemble?
NO
t2
t1

28. Why they work?
• Reasons for their good results:
• Statistical reasons: There are not enough data for
the classification algorithm to obtain an optimum
hypothesis.
• Computational reasons: The single algorithm is
not capable of reaching the optimum solution.
• Expressive reasons: The solution is outside the
hypothesis space.
28/63!

29. Why they work?
Thomas Dietterich!

30. Why they work?
30/63!
A set of suboptimal solutions can be created that
compensate their limitations when combined in the
ensemble.!

31. Success story 1: Netflix prize
challenge
• Dataset: rating of 17770 movies and 480189 users
Combines
hundreds of
models from three
teams
Variant of stacking

32. Success story 2: KDD cup
• KDD cup 2013: Predict papers written by given author.
• The winning team used Random Forest and
Boosting among other models combined with
regularized linear regression.
• KDD cup 2014: Predict funding requests that deserve an
A+ in donorschoose.org
• Multistage ensemble
• KDD cup 2015: Predict dropouts in MOOC
• Multistage ensemble

33. Success story 3: Kinect
• Computer Vision
• Classify pixels into body parts (leg, head, etc)
• Use Random Forests

34. 34!
• A family of machine learning algorithms with one of
the best over all performances. Comparable or better
than SVMs
• Almost parameter less learning algorithms.
• If decision trees are the base learners, they are cheap
(fast) to train and in test.
Good things about ensembles

35. 35!
• None! Well maybe something…
• Slower than single classifier. Since we create
hundreds or thousands of classifiers.
• Can be mitigated using ensemble pruning
Bad things about ensembles