The document discusses the application of Lie group and Lie algebra concepts in robot mechanics, focusing on motion representation, kinematics, and dynamics. Key topics include differential manifolds, forward kinematics, and inverse dynamics, utilizing the product of exponentials and the Jacobian for angular velocity. The summary also highlights the differences between Lie groups and other notational systems for describing rigid body dynamics.

1. Terry Taewoong Um (terry.t.um@gmail.com)
University of Waterloo
Department of Electrical & Computer Engineering
Terry Taewoong Um
LIE GROUP FORMULATION
FOR ROBOT MECHANICS
1

2. Terry Taewoong Um (terry.t.um@gmail.com)
CONTENTS
1. Motion and Lie Group
2. Kinematics and Dynamics
3. Summary + Q&A
2

3. Terry Taewoong Um (terry.t.um@gmail.com)
CONTENTS
3
1. Motion and Lie Group

4. Terry Taewoong Um (terry.t.um@gmail.com)
MOTIVATION
4
• Coordinate-free approach
http://arxiv.org/pdf/1404.1100.pdf
- Which coordinate should we choose?
- Let’s remove the dependency on the choice of reference frames!
→ Use the right representation for motion → Lie group & Lie algebra
[Newton-Euler formulation]
- Geodesic : a shortest path b/w two points
- Euler angle-based trajectory is not a geodesic!

5. Terry Taewoong Um (terry.t.um@gmail.com)
PRELIMINARY
5
• Differential Manifolds
Implicit representation
Explicit representation
Local
coordinate
n-dim manifold is a set that locally resembles n-dim Euclidean space
- Each point of an n-dimensional manifold has a neighbourhood that is
homeomorphic to the Euclidean space of dimension n.
Local coordinate : vector space! Riemannian metric
Minimal geodesics
distortion

6. Terry Taewoong Um (terry.t.um@gmail.com)
6
- General Linear Group, GL(n)
: 𝑛 × 𝑛 invertible matrices with matrix multiplication
PRELIMINARY
- Special Linear Group, SL(n) : GL(n) with determinant 1
- Orthogonal Group, O(n) : 𝑄 ∈ 𝐺𝐿 𝑛 𝑄 𝑇
𝑄 = 𝑄𝑄 𝑇
= 𝐼}
• Lie Group : a group that is also a differentiable manifold
e.g.)
• Lie Algebra : the tangent space at the identity of Lie group
a vector space with Lie bracket operation [x, y]
- Lie bracket
Non-commutative
Lie group
Lie algebra

7. Terry Taewoong Um (terry.t.um@gmail.com)
7
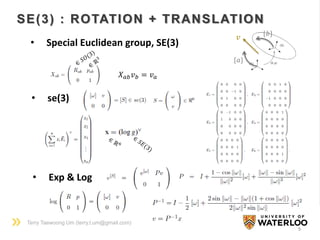
SO(3) : ROTATION
• Special Orthogonal group, SO(3)
𝑅 𝑇
𝑅 = 𝑅𝑅 𝑇
= 𝐼det 𝑅 = 1
• Lie algebra of SO(3) : so(3)
𝑅 𝑎𝑏 = [𝑥 𝑎 𝑦𝑎 𝑧 𝑎]
𝑥
𝑦
𝑧
𝑥 of {b} w.r.t. {a}
- You can express SO(3) with the rotation axis & angle!
http://goo.gl/uqilDV
so(3) : skew-symm. matrices
• Exponential mapping
exp ∶ 𝑠𝑜 3 → 𝑆𝑂(3) exp ∶ 𝑠𝑒 3 → 𝑆𝐸(3)
exp ∶ 𝐿𝑖𝑒 𝑎𝑙𝑔𝑒𝑏𝑟𝑎 → 𝐿𝑖𝑒 𝑔𝑟𝑜𝑢𝑝
𝑅 𝑎𝑏 𝑣 𝑏 = 𝑣 𝑎

8. Terry Taewoong Um (terry.t.um@gmail.com)
8
SO(3) : ROTATION
• Exponential mapping (Cont.)
e.g.) 𝑅𝑜𝑡 𝑧, 𝜃 = 𝐼 + 𝑠𝑖𝑛𝜃
0 −1 0
1 0 0
0 0 0
+ (1 − 𝑐𝑜𝑠𝜃)
0 −1 0
1 0 0
0 0 0
0 −1 0
1 0 0
0 0 0
=
1 0 0
0 1 0
0 0 1
+
0 −𝑠𝑖𝑛𝜃 0
𝑠𝑖𝑛𝜃 0 0
0 0 0
+ (1 − 𝑐𝑜𝑠𝜃)
−1 0 0
0 −1 0
0 0 0
=
𝑐𝑜𝑠𝜃 −𝑠𝑖𝑛𝜃 0
𝑠𝑖𝑛𝜃 𝑐𝑜𝑠𝜃 0
0 0 1
• Logarithm mapping log : 𝐿𝑖𝑒 𝑔𝑟𝑜𝑢𝑝 → 𝐿𝑖𝑒 𝑎𝑙𝑔𝑒𝑏𝑟𝑎

9. Terry Taewoong Um (terry.t.um@gmail.com)
9
SE(3) : ROTATION + TRANSLATION
• Special Euclidean group, SE(3)
𝑋 𝑎𝑏 𝑣 𝑏 = 𝑣 𝑎
• Exp & Log
• se(3)
𝑣
{𝑏}
{𝑎}

10. Terry Taewoong Um (terry.t.um@gmail.com)
10
ADJOINT MAPPING
• Lie Algebra : the tangent space at the identity of Lie group
a vector space with Lie bracket operation [x, y]
• Small adjoint mapping
• Large adjoint mapping
cross product
For so(3),
For se(3),
For so(3),
For se(3),
coordinate change

11. Terry Taewoong Um (terry.t.um@gmail.com)
CONTENTS
11
2. Kinematics & Dynamics

12. Terry Taewoong Um (terry.t.um@gmail.com)
12
FORWARD KINEMATICS
• Product of Exponential (POE) Formula
- D-H Convention
- POE formula from robot configuration
h = pitch (m/𝑟𝑎𝑑) (0 for rev. joint)
q = a point on the axis
variableconstant
c.f.)
A seen from {0}
𝑅 𝑎𝑏 𝑣 𝑏 = 𝑣 𝑎
𝑇𝑎𝑏 𝑣 𝑏 = 𝑣 𝑎
𝐴𝑑 𝑇 𝑎𝑏
[𝐴] 𝑏= [𝐴] 𝑎
Coord. change
SE(3) from {0} to {n} at home position

13. Terry Taewoong Um (terry.t.um@gmail.com)
13
FORWARD KINEMATICS

14. Terry Taewoong Um (terry.t.um@gmail.com)
14
DIFFERENTIAL KINEMATICS
• Angular velocity by rotational motion
from space(fixed frame) to body
c.f.)
body velocity
𝝎/𝒗 : angular/linear velocity of the {body} attached to
the body relative to the {space} but expressed @{body}
• Spatial velocity by screw motion
• Jacobian
From
𝜃 = 𝐽𝑠 𝜃

15. Terry Taewoong Um (terry.t.um@gmail.com)
15
PRELIMINARY FOR DYNAMICS
• Coordinate transformation rules
for velocity-like se(3) for force-like se(3)
generalized momentum
dual map
c
• Time derivatives
: :
c.f.)
whole
derivative
component-wise
derivative
𝑉 is required

16. Terry Taewoong Um (terry.t.um@gmail.com)
16
INVERSE DYNAMICS
• 𝑽 :
• 𝑽 : c.f.)
• 𝑭𝒐𝒓𝒄𝒆 ∶
propagated forces

17. Terry Taewoong Um (terry.t.um@gmail.com)
17
INVERSE DYNAMICS

18. Terry Taewoong Um (terry.t.um@gmail.com)
CONTENTS
18
3. Summary + Q&A

19. Terry Taewoong Um (terry.t.um@gmail.com)
19
SUMMARY
• Lie Group : a group that is also a differentiable manifold
• Lie Algebra : the tangent space at the identity of Lie group
• SO(3), so(3), SE(3), se(3), exp, log, Ad, ad
coord. trans.
for se(3)
cross product
for se(3)
• Forward Kinematics
• Lie algebra is vector space! (easier to apply pdf)
• Inverse Dynamics
• Differential Kinematics
𝜃 = 𝐽𝑠 𝜃

20. Terry Taewoong Um (terry.t.um@gmail.com)
20
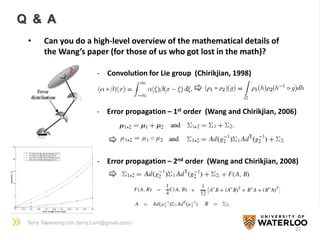
Q & A
• What are the benefits/drawbacks of using Lie group for rigid
body dynamics?
• What are the key differences between Lie groups and other 6D
formulations (e.g., Featherstone's spatial notation)?
[Featherstone's cross operation]
skew-symmetric
Lie bracket

21. Terry Taewoong Um (terry.t.um@gmail.com)
21
Q & A
[From Featherstone's book]

22. Terry Taewoong Um (terry.t.um@gmail.com)
22
Q & A
• Can you do a high-level overview of the mathematical details of
the Wang’s paper (for those of us who got lost in the math)?
? - Convolution for Lie group (Chirikjian, 1998)
- Error propagation – 1st order (Wang and Chirikjian, 2006)
- Error propagation – 2nd order (Wang and Chirikjian, 2008)

23. Terry Taewoong Um (terry.t.um@gmail.com)
23
Thank you