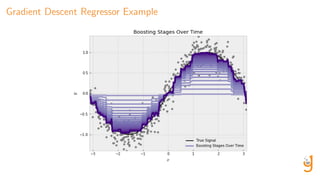
This document compares and contrasts boosting with other ensemble methods such as bagging and random forests. It discusses two specific boosting algorithms - AdaBoost, which fits models on weighted labels, and gradient boosting, which fits models on residuals from previous models. Both aim to produce low bias, low variance predictions by building models sequentially. The document provides pseudocode for AdaBoost classification and gradient boosting regression, and explains how boosting methods work to improve upon previous predictions at each step of the ensemble.

1. Boosting
An Ensemble Learning Method
Kirkwood Donavin & Galvanize Inc.
13th of December, 2017

2. Learning Objectives
Compare and contrast boosting with other ensemble methods
Differences between AdaBoost and Gradient Boosting
Boosting algorithm for both classification and regression

3. It’s Test Time!
How might an ensemble of DSI
students complete a single
assessment as if they were a
machine learning algorithm?
Concurrently work on (copies
of) the exam, and then
aggregate responses
Assume students are strong
learners (i.e., generally correct on
average, with some mistakes).
Would each student be high or
low bias estimator? Would
each student be a low or high
variance estimator?

4. An Unconventional Strategy
Now, instead of working in parallel on multiple exams, there is one exam on which each
student may have a very limited amount of time to complete in sequence.
In between estimators (students) the scorer (me) comes and marks answers that are
incorrect, and then passes the marked exam to the to the next learner.
Now, is each estimator (student) high or low bias? low or high variance?

5. Ensemble Methods
Goal: to improve generalizability by combining the predictions of several
estimators to produce a single prediction. There are two families:
1. Averaging Methods - high-variance estimators’ predictions are aggregated to produce a
single low-variance prediction (e.g., bagging, random forests)
2. Boosting Methods - high-bias estimator predictions are built on top of each other,
sequentially until a low-bias prediction is achieved
Similarity: Both have the goal of arriving at low-bias, low-variance predictions

6. Boosted Trees
A Different Ensemble Approach
The ensemble of decision trees (i.e., the weak estimators) are ‘grown’ sequentially, based
on the results of prior estimator prediction scores
Importantly, each new estimator is fit on a modified version of the training set, based
on the results of the prior tree
Each tree is a weak learner on purpose, that way variance between estimators is low
Check for Understanding with a Partner: What are the similarities and differences
between boosting and bagging? Random forest?

7. Two Boosting Algorithms
AdaBoost (Adaptive Boost): In between weak estimators (e.g., decision trees of depth
1) the labels (yi ) are weighted by the amount of times they are mis-classified, or the
magnitude of their residual error.
Gradient Boost: The training data passed from one weak estimator to another are
residuals from the prior estimator
Note: Either of these algorithms may be applied to classification or regression problems

8. Discrete AdaBoost Classification Algorithm
Given an input training set, (xi , yi )n
i=1, a weighted loss function L(y, F(x), w) where F(·) is a weak classifier, and a number of
estimators, M.
1. Initialize the observation weights: wi = 1
N , i = 1, 2, . . . , N
2. For m = 1 to M estimators:
(a) Fit a weak classifier Fm(x): (e.g., decision tree of depth 1) to the weighted training data
that minimizes the weighted loss function, L(y, Fm(·), w).
(b) Compute the weighted error rate for classifier m:
εm =
N
i wi · I [yi = Fm(xi )]
N
i wi
(c) Compute tree weighting factor:
αm = log
1 − εm
εm
(d) Update training data weights:
wi ← wi · exp {αm · I [yi = Fm(xi )]} , for i = 1, 2, . . . , N
3. Finally, output the sign of the weighted sum of models 1 . . . , M:
F(X) = sign
M
m=1
αmFm(X)
E.g., Fm(xi ) = arg min
F(·)
N
i wi · I [yi = F(xi )]
A measure of each
weak learner’s
classification success

9. AdaBoost Classification Example

10. Gradient Descent Regressor Algorithm
Given an input training set, (xi , yi )n
i=1, a differentiable loss function L(y, G(X)) where G(·) is a weak regressor, and a number
of estimators, M.
1. Initialize model with a constant value:
G0(X) = arg min
γ
n
i
L(yi , γ)
= ¯y
2. For m = 1 to M:
(a) Compute the pseudo-residuals:
ri,m = −
∂L(yi , Gm−1(xi ))
∂Gm−1(xi )
for i = 1, . . . , n
(b) Fit a high-bias learner, Gm(X) to pseudo-residuals.
(c) Calculate a weighting multiplier:
γm = arg min
γ
n
i=1
L(yi , Gm−1(xi ) + γGm(xi ))
3. Finally, combine the weighted estimators:
G(X) =
M
m=1
γmGm(X)
E.g., L(y, G(X)) = i
1
2 [yi − G(xi )]2
,
where G(·) is a decision tree of depth 1
i.e., the gradient part!
Train with (xi , ri,m)n
i=1
(instead of y)
The greater the
loss-improvement, the
higher the weight

11. Gradient Descent Regressor Example

12. Recap
You should now feel comfortable doing the following:
Comparing and contrasting boosting with other ensemble methods (e.g., bagging, random
forest)
Name the characteristic differences between AdaBoost and Gradient Boosting.
fitted on weighted labels versus residuals
And, how are they similar?
Write pseudo-code for the Discrete AdaBoost Classification algorithm, and the Gradient
Descent Regressor algorithm (with the assistance of the slides above, of course)

13. Acknowledgments
Galvanize, Inc. for instructional material
My Galvanize Data Science Instructors: Taryn Heilman & Jon Courtney for education and
guidance
Presentation created with LATEX’s Beamer package