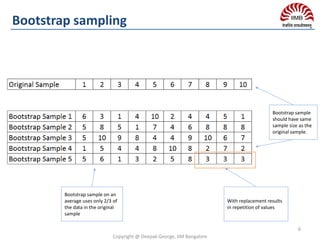
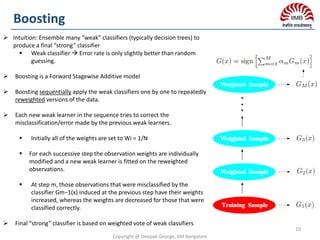
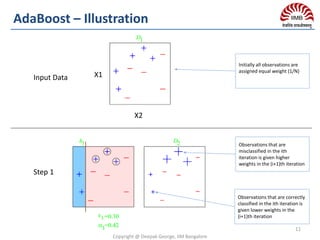
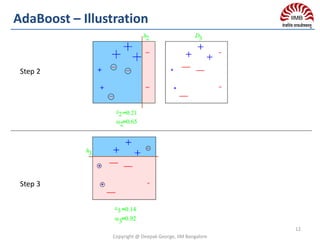
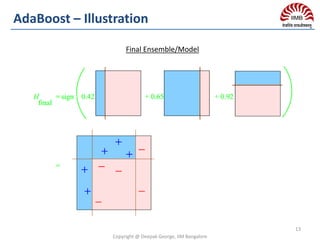
This document provides a summary of Deepak George's background and experience in data science and machine learning. It includes information about his education such as degrees from College of Engineering Trivandrum and Indian Institute of Management Bangalore. It also lists his work experience at companies like Mu Sigma and Accenture Analytics. Additionally, it outlines some of Deepak's data science projects and accomplishments, as well as his contact information.



![ Problem: Decision tree have low bias & suffer from high variance
Goal: Reduce variance of decision trees
Hint: Given set of n independent observations Z1, . . . , Zn, each
with variance σ2, the variance of the mean of the observations is given
by σ2/n.
In other words, averaging a set of observations reduces variance.
Theoretically: Take multiple independent samples S’ from the population
Fit “bushy”/deep decision trees on each S1,S2…. Sn
Trees are grown deep and are not pruned
Variance reduces linearly & Bias remain unchanged
Practically: We only have one sample/training set & not the population.
So take bootstrap samples i.e. multiple samples from the
single sample with replacement
Variance reduces sub-linearly & Bias often increase slightly
because bootstrap samples are correlated.
Final Classifier: Average of predictions for regression or majority vote
for classification.
High Variance introduced by deep decision trees are mitigated by
averaging predictions from each decision trees.
Copyright @ Deepak George, IIM Bangalore
5
Bagging
Population
Alice# 14# 0# 1#
Bob# 10# 1# 1#
Carol# 13# 0# 1#
Dave# 8# 1# 0#
Erin# 11# 0# 0#
Frank# 9# 1# 1#
Gena# 8# 0# 0#
James# 11# 1# 1#
Jessica# 14# 0# 1#
Alice# 14# 0# 1#
Amy# 12# 0# 1#
Bob# 10# 1# 1#
Xavier# 9# 1# 0#
Cathy# 9# 0# 1#
Carol# 13# 0# 1#
Eugene# 13# 1# 0#
Rafael# 12# 1# 1#
Dave# 8# 1# 0#
Peter# 9# 1# 0#
Henry# 13# 1# 0#
Erin# 11# 0# 0#
Rose# 7# 0# 0#
Iain# 8# 1# 1#
Paulo# 12# 1# 0#
Margaret# 10# 0# 1#
Frank# 9# 1# 1#
Jill# 13# 0# 0#
Leon# 10# 1# 0#
Sarah# 12# 0# 0#
Gena# 8# 0# 0#
Patrick# 5# 1# 1# L(h)#=#E(x,y)~P(x,y)[#f(h(x),y)#]###
Alice# 14# 0# 1#
Bob# 10# 1# 1#
Carol# 13# 0# 1#
Dave# 8# 1# 0#
Erin# 11# 0# 0#
Frank# 9# 1# 1#
Gena# 8# 0# 0#
James# 11# 1# 1#
Jessica# 14# 0# 1#
Alice# 14# 0# 1#
Amy# 12# 0# 1#
Bob# 10# 1# 1#
Xavier# 9# 1# 0#
Cathy# 9# 0# 1#
Carol# 13# 0# 1#
Eugene# 13# 1# 0#
Rafael# 12# 1# 1#
Dave# 8# 1# 0#
Peter# 9# 1# 0#
Henry# 13# 1# 0#
Erin# 11# 0# 0#
Rose# 7# 0# 0#
Iain# 8# 1# 1#
Paulo# 12# 1# 0#
Margaret# 10# 0# 1#
Frank# 9# 1# 1#
Jill# 13# 0# 0#
Leon# 10# 1# 0#
Sarah# 12# 0# 0#
Gena# 8# 0# 0#
Patrick# 5# 1# 1# L(h)#=#E(x,y)~P(x,y)[#f(h(x),y)#]###
S1
Alice# 14# 0# 1#
Bob# 10# 1# 1#
Carol# 13# 0# 1#
Dave# 8# 1# 0#
Erin# 11# 0# 0#
Frank# 9# 1# 1#
Gena# 8# 0# 0#
James# 11# 1# 1#
Jessica# 14# 0# 1#
Alice# 14# 0# 1#
Amy# 12# 0# 1#
Bob# 10# 1# 1#
Xavier# 9# 1# 0#
Cathy# 9# 0# 1#
Carol# 13# 0# 1#
Eugene# 13# 1# 0#
Rafael# 12# 1# 1#
Dave# 8# 1# 0#
Peter# 9# 1# 0#
Henry# 13# 1# 0#
Erin# 11# 0# 0#
Rose# 7# 0# 0#
Iain# 8# 1# 1#
Paulo# 12# 1# 0#
Margaret# 10# 0# 1#
Frank# 9# 1# 1#
Jill# 13# 0# 0#
Leon# 10# 1# 0#
Sarah# 12# 0# 0#
Gena# 8# 0# 0#
Patrick# 5# 1# 1# L(h)#=#E(x,y)~P(x,y)[#f(h(x),y)#]###
S2
Alice# 14# 0# 1#
Bob# 10# 1# 1#
Carol# 13# 0# 1#
Dave# 8# 1# 0#
Erin# 11# 0# 0#
Frank# 9# 1# 1#
Gena# 8# 0# 0#
James# 11# 1# 1#
Jessica# 14# 0# 1#
Alice# 14# 0# 1#
Amy# 12# 0# 1#
Bob# 10# 1# 1#
Xavier# 9# 1# 0#
Cathy# 9# 0# 1#
Carol# 13# 0# 1#
Eugene# 13# 1# 0#
Rafael# 12# 1# 1#
Dave# 8# 1# 0#
Peter# 9# 1# 0#
Henry# 13# 1# 0#
Erin# 11# 0# 0#
Rose# 7# 0# 0#
Iain# 8# 1# 1#
Paulo# 12# 1# 0#
Margaret# 10# 0# 1#
Frank# 9# 1# 1#
Jill# 13# 0# 0#
Leon# 10# 1# 0#
Sarah# 12# 0# 0#
Gena# 8# 0# 0#
Patrick# 5# 1# 1# L(h)#=#E(x,y)~P(x,y)[#f(h(x),y)#]###
Sn
.
.
.
Samples
Sample
Alice# 14# 0# 1#
Bob# 10# 1# 1#
Carol# 13# 0# 1#
Dave# 8# 1# 0#
Erin# 11# 0# 0#
Frank# 9# 1# 1#
Gena# 8# 0# 0#
James# 11# 1# 1#
Jessica# 14# 0# 1#
Alice# 14# 0# 1#
Amy# 12# 0# 1#
Bob# 10# 1# 1#
Xavier# 9# 1# 0#
Cathy# 9# 0# 1#
Carol# 13# 0# 1#
Eugene# 13# 1# 0#
Rafael# 12# 1# 1#
Dave# 8# 1# 0#
Peter# 9# 1# 0#
Henry# 13# 1# 0#
Erin# 11# 0# 0#
Rose# 7# 0# 0#
Iain# 8# 1# 1#
Paulo# 12# 1# 0#
Margaret# 10# 0# 1#
Frank# 9# 1# 1#
Jill# 13# 0# 0#
Leon# 10# 1# 0#
Sarah# 12# 0# 0#
Gena# 8# 0# 0#
Patrick# 5# 1# 1# L(h)#=#E(x,y)~P(x,y)[#f(h(x),y)#]###
S1
Alice# 14# 0# 1#
Bob# 10# 1# 1#
Carol# 13# 0# 1#
Dave# 8# 1# 0#
Erin# 11# 0# 0#
Frank# 9# 1# 1#
Gena# 8# 0# 0#
James# 11# 1# 1#
Jessica# 14# 0# 1#
Alice# 14# 0# 1#
Amy# 12# 0# 1#
Bob# 10# 1# 1#
Xavier# 9# 1# 0#
Cathy# 9# 0# 1#
Carol# 13# 0# 1#
Eugene# 13# 1# 0#
Rafael# 12# 1# 1#
Dave# 8# 1# 0#
Peter# 9# 1# 0#
Henry# 13# 1# 0#
Erin# 11# 0# 0#
Rose# 7# 0# 0#
Iain# 8# 1# 1#
Paulo# 12# 1# 0#
Margaret# 10# 0# 1#
Frank# 9# 1# 1#
Jill# 13# 0# 0#
Leon# 10# 1# 0#
Sarah# 12# 0# 0#
Gena# 8# 0# 0#
Patrick# 5# 1# 1# L(h)#=#E(x,y)~P(x,y)[#f(h(x),y)#]###
S2
Alice# 14# 0# 1#
Bob# 10# 1# 1#
Carol# 13# 0# 1#
Dave# 8# 1# 0#
Erin# 11# 0# 0#
Frank# 9# 1# 1#
Gena# 8# 0# 0#
James# 11# 1# 1#
Jessica# 14# 0# 1#
Alice# 14# 0# 1#
Amy# 12# 0# 1#
Bob# 10# 1# 1#
Xavier# 9# 1# 0#
Cathy# 9# 0# 1#
Carol# 13# 0# 1#
Eugene# 13# 1# 0#
Rafael# 12# 1# 1#
Dave# 8# 1# 0#
Peter# 9# 1# 0#
Henry# 13# 1# 0#
Erin# 11# 0# 0#
Rose# 7# 0# 0#
Iain# 8# 1# 1#
Paulo# 12# 1# 0#
Margaret# 10# 0# 1#
Frank# 9# 1# 1#
Jill# 13# 0# 0#
Sn
.
.
.
Bootstrap Samples
Alice# 14# 0# 1#
Bob# 10# 1# 1#
Carol# 13# 0# 1#
Dave# 8# 1# 0#
Erin# 11# 0# 0#
Frank# 9# 1# 1#
Gena# 8# 0# 0#
James# 11# 1# 1#
Jessica# 14# 0# 1#
Alice# 14# 0# 1#
Amy# 12# 0# 1#
Bob# 10# 1# 1#
Xavier# 9# 1# 0#
Cathy# 9# 0# 1#
Carol# 13# 0# 1#
Eugene# 13# 1# 0#
Rafael# 12# 1# 1#
Dave# 8# 1# 0#
Peter# 9# 1# 0#
Henry# 13# 1# 0#
Erin# 11# 0# 0#
Rose# 7# 0# 0#
Iain# 8# 1# 1#
Paulo# 12# 1# 0#
Margaret# 10# 0# 1#
Frank# 9# 1# 1#
Jill# 13# 0# 0#
Leon# 10# 1# 0#
Sarah# 12# 0# 0#
Gena# 8# 0# 0#
Patrick# 5# 1# 1# L(h)#=#E(x,y)~P(x,y)[#f(h(x),y)#]###](https://image.slidesharecdn.com/decisiontreeensembles-iimb-151220043843/85/Decision-Tree-Ensembles-Bagging-Random-Forest-Gradient-Boosting-Machines-5-320.jpg)