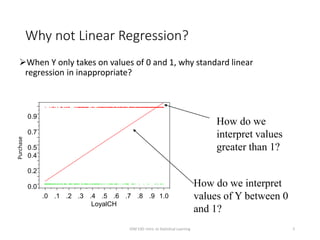
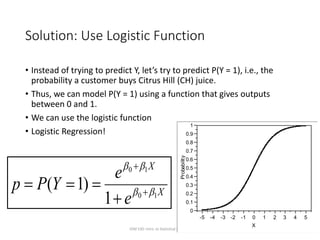
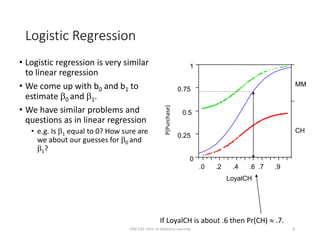
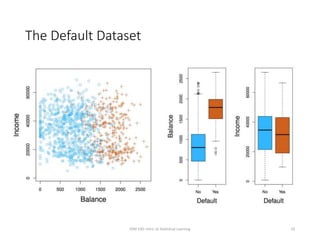
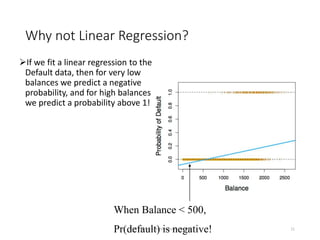
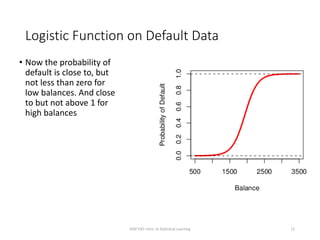
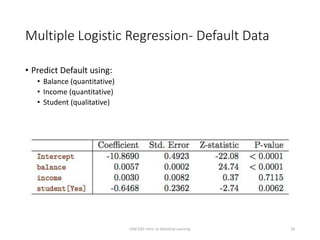
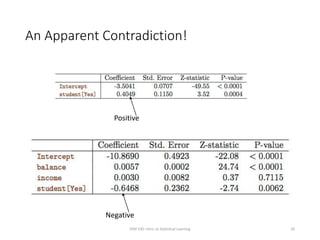
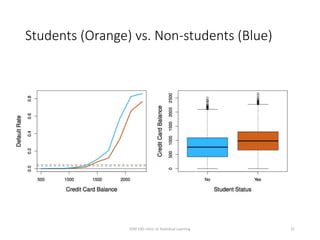
This document provides an overview of logistic regression for classification problems. It introduces logistic regression using two examples: predicting orange juice brand preference and credit card default. Linear regression is inappropriate for classification with binary outcomes. Logistic regression models the probability of an outcome using a logistic function to constrain predictions between 0 and 1. The document explains how to interpret logistic regression coefficients and make predictions, and how to extend the approach to multiple predictors.

1. Classification Methods
Chapter 04 (part 01)
IOM 530: Intro. to Statistical Learning 1

2. Logistic Regression
IOM 530: Intro. to Statistical Learning 2

3. Outline
Cases:
Orange Juice Brand Preference
Credit Card Default Data
Why Not Linear Regression?
Simple Logistic Regression
Logistic Function
 Interpreting the coefficients
Making Predictions
Adding Qualitative Predictors
Multiple Logistic Regression
IOM 530: Intro. to Statistical Learning 3

4. Case 1: Brand Preference for Orange Juice
• We would like to predict what customers prefer to buy: Citrus Hill or
Minute Maid orange juice?
• The Y (Purchase) variable is categorical: 0 or 1
• The X (LoyalCH) variable is a numerical value (between 0 and 1)
which specifies the how much the customers are loyal to the Citrus
Hill (CH) orange juice
• Can we use Linear Regression when Y is categorical?
IOM 530: Intro. to Statistical Learning 4

5. Why not Linear Regression?
When Y only takes on values of 0 and 1, why standard linear
regression in inappropriate?
IOM 530: Intro. to Statistical Learning 5
0.0
0.2
0.4
0.5
0.7
0.9
.0 .1 .2 .3 .4 .5 .6 .7 .8 .9 1.0
LoyalCH
Purchase
How do we interpret
values of Y between 0
and 1?
How do we
interpret values
greater than 1?

6. Problems
• The regression line 0+1X can take on any value between negative
and positive infinity
• In the orange juice classification problem, Y can only take on two
possible values: 0 or 1.
• Therefore the regression line almost always predicts the wrong value
for Y in classification problems
IOM 530: Intro. to Statistical Learning 6

7. Solution: Use Logistic Function
• Instead of trying to predict Y, let’s try to predict P(Y = 1), i.e., the
probability a customer buys Citrus Hill (CH) juice.
• Thus, we can model P(Y = 1) using a function that gives outputs
between 0 and 1.
• We can use the logistic function
• Logistic Regression!
IOM 530: Intro. to Statistical Learning 7
X
X
e
e
YPp 10
10
1
)1( 





0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Probability
-5 -4 -3 -2 -1 0 1 2 3 4 5
X

8. Logistic Regression
• Logistic regression is very similar
to linear regression
• We come up with b0 and b1 to
estimate 0 and 1.
• We have similar problems and
questions as in linear regression
• e.g. Is 1 equal to 0? How sure are
we about our guesses for 0 and
1?
IOM 530: Intro. to Statistical Learning 8
0
0.25
0.5
0.75
1
.0 .2 .4 .6 .7 .9
LoyalCH
CH
MM
If LoyalCH is about .6 then Pr(CH)  .7.
P(Purchase)

9. Case 2: Credit Card Default Data
We would like to be able to predict customers that are likely to
default
Possible X variables are:
Annual Income
Monthly credit card balance
The Y variable (Default) is categorical: Yes or No
How do we check the relationship between Y and X?
IOM 530: Intro. to Statistical Learning 9

10. The Default Dataset
IOM 530: Intro. to Statistical Learning 10

11. Why not Linear Regression?
If we fit a linear regression to the
Default data, then for very low
balances we predict a negative
probability, and for high balances
we predict a probability above 1!
IOM 530: Intro. to Statistical Learning 11
When Balance < 500,
Pr(default) is negative!

12. Logistic Function on Default Data
• Now the probability of
default is close to, but
not less than zero for
low balances. And close
to but not above 1 for
high balances
IOM 530: Intro. to Statistical Learning 12

13. Interpreting 1
• Interpreting what 1 means is not very easy with logistic regression,
simply because we are predicting P(Y) and not Y.
• If 1 =0, this means that there is no relationship between Y and X.
• If 1 >0, this means that when X gets larger so does the probability
that Y = 1.
• If 1 <0, this means that when X gets larger, the probability that Y = 1
gets smaller.
• But how much bigger or smaller depends on where we are on the
slope
IOM 530: Intro. to Statistical Learning 13

14. Are the coefficients significant?
• We still want to perform a hypothesis test to see whether we can be
sure that are 0 and 1 significantly different from zero.
• We use a Z test instead of a T test, but of course that doesn’t change
the way we interpret the p-value
• Here the p-value for balance is very small, and b1 is positive, so we
are sure that if the balance increase, then the probability of default
will increase as well.
IOM 530: Intro. to Statistical Learning 14

15. Making Prediction
• Suppose an individual has an average balance of $1000. What is their
probability of default?
• The predicted probability of default for an individual with a balance
of $1000 is less than 1%.
• For a balance of $2000, the probability is much higher, and equals to
0.586 (58.6%).
IOM 530: Intro. to Statistical Learning 15

16. Qualitative Predictors in Logistic Regression
• We can predict if an individual default by checking if she is a student
or not. Thus we can use a qualitative variable “Student” coded as
(Student = 1, Non-student =0).
• b1 is positive: This indicates students tend to have higher default
probabilities than non-students
IOM 530: Intro. to Statistical Learning 16

17. Multiple Logistic Regression
• We can fit multiple logistic just like regular regression
IOM 530: Intro. to Statistical Learning 17

18. Multiple Logistic Regression- Default Data
• Predict Default using:
• Balance (quantitative)
• Income (quantitative)
• Student (qualitative)
IOM 530: Intro. to Statistical Learning 18

19. Predictions
• A student with a credit card balance of $1,500 and an income of
$40,000 has an estimated probability of default
IOM 530: Intro. to Statistical Learning 19

20. An Apparent Contradiction!
IOM 530: Intro. to Statistical Learning 20
Positive
Negative

21. Students (Orange) vs. Non-students (Blue)
IOM 530: Intro. to Statistical Learning 21

22. To whom should credit be offered?
• A student is risker than non students if no information about the
credit card balance is available
• However, that student is less risky than a non student with the same
credit card balance!
IOM 530: Intro. to Statistical Learning 22