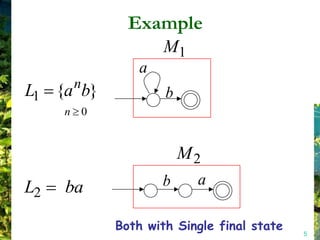
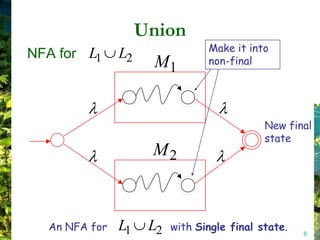
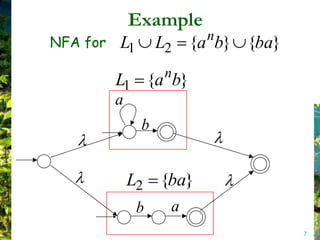
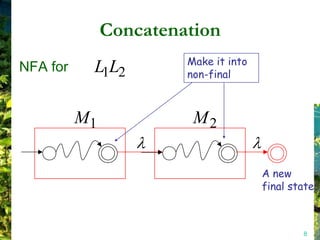
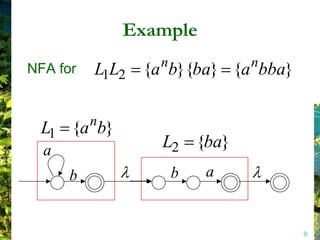
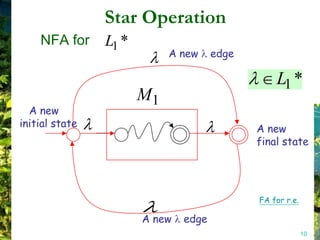
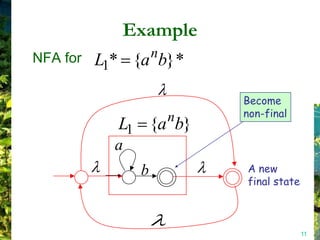
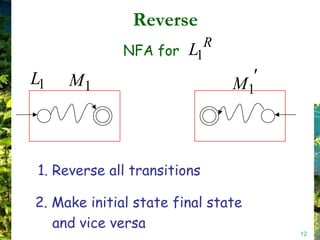
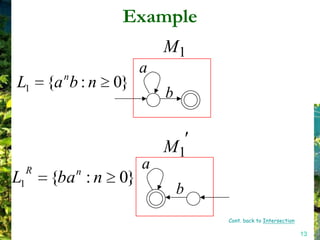
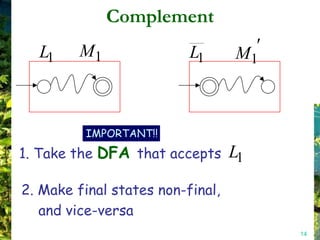
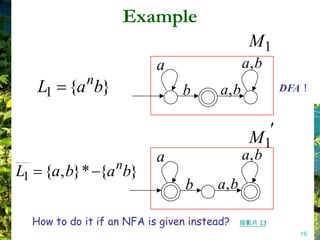
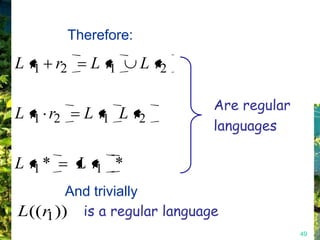
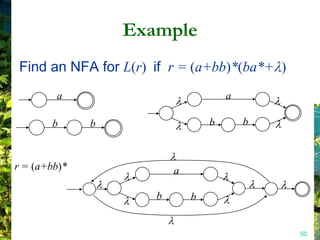
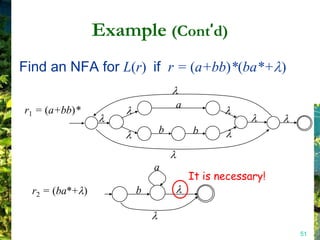
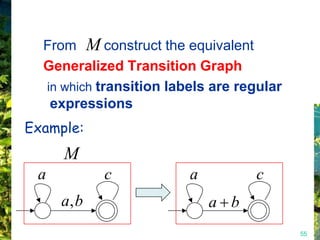
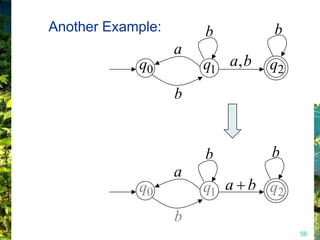
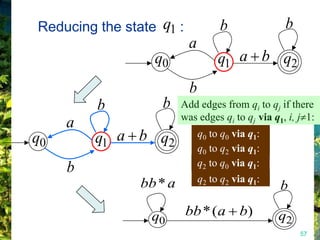
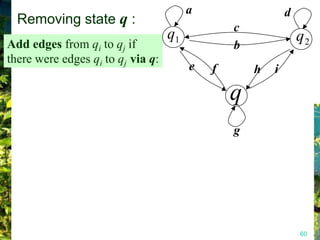
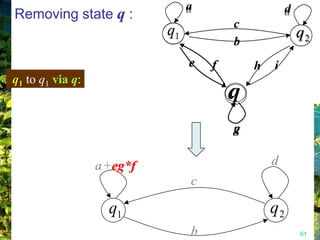
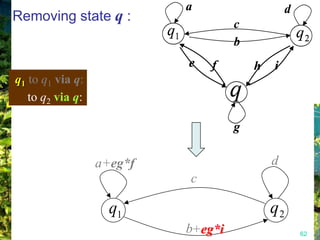
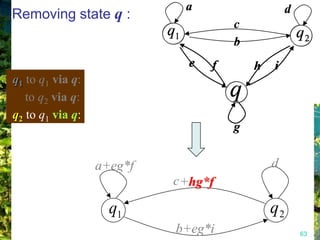
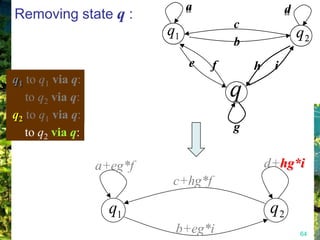
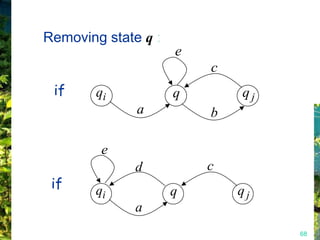
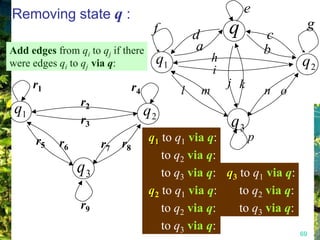
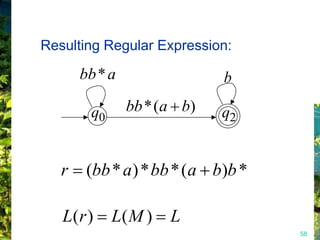This document discusses closure properties of regular languages under various operations. It proves that regular languages are closed under union, concatenation, Kleene star, reversal, complement, and intersection by constructing non-deterministic finite automata (NFAs) to recognize the languages resulting from these operations. Examples are provided to illustrate the constructions of NFAs for union, concatenation, Kleene star, and reversal. The document also discusses using DeMorgan's laws to show closure under complement and intersection.

1. Closure Properties of
Regular Languages
This is the partial material
from Section 4.1, 3.1 & 3.2
1

2. For regular languages L1 and L2
we will prove that:
Union: L1 L2
Concatenation: L1L2
Star: are regular
L1 *
Languages
Reversal: L1R
Complement: L1
Intersection: L1 L2 2

3. We say: Regular languages are closed under
Union: L1 L2
Concatenation: L1L2
Star: L1 *
Reversal: L1R
Complement: L1
Intersection: L1 L2 3

4. Regular language L1 Regular language L2
L M1 L1 L M2 L2
NFA M1 NFA M2
Single final state Single final state
4

5. Example
M1
a
n
L1 {a b} b
n 0
M2
L2 ba b a
Both with Single final state 5

6. Union
Make it into
NFA for L1 L2 non-final
M1
New final
state
M2
An NFA for L1 L2 with Single final state.
6

7. Example
n
NFA for L1 L2 {a b} {ba}
n
L1 {a b}
a
b
L2 {ba}
b a
7

8. Concatenation
Make it into
NFA for L1L2 non-final
M1 M2
A new
final state
8

9. Example
n n
NFA for L1L2 {a b}{ba} {a bba}
n
L1 {a b}
a L2 {ba}
b b a
9

10. Star Operation
NFA for L1 *
A new edge
L1 *
M1
A new
initial state A new
final state
FA for r.e.
A new edge
10

11. Example
NFA for n
L1* {a b} *
Become
n non-final
L1 {a b}
a
b A new
final state
11

12. Reverse
R
NFA for L1
L1 M1 M1
1. Reverse all transitions
2. Make initial state final state
and vice versa
12

13. Example
M1
n
a
L1 {a b : n 0}
b
M1
R n
a
L1 {ba : n 0}
b
Cont. back to Intersection
13

14. Complement
L1 M1 L1 M1
IMPORTANT!!
1. Take the DFA that accepts L1
2. Make final states non-final,
and vice-versa
14

15. Example
M1
a a, b
n
L1 {a b} b a, b DFA！
M1
a a, b
n
L1 {a, b} * {a b}
b a, b
How to do it if an NFA is given instead? 投影片 13
15

16. Intersection
DeMorgan’s Law: L1 L2 L1 L2
L1 , L2 regular
L1 , L2 regular
L1 L2 regular
L1 L2 regular
L1 L2 regular
16

17. Example
L1 {a b} regular
n
L1 L2 {ab}
L2 {ab, ba} regular regular
The cor of two languages is
cor ( L1 , L2 ) {w : w L1 or w L2 }
Show that the family of regular languages is closed
under the cor operation.
17

18. A Construction way for L1 L2
disjoint same
L1 L( M 1 ) with DFA M 1 (Q, , 1 , q0 , F1 )
L2 L( M 2 ) with DFA M 2 ( P, , 2 , p0 , F2 )
ˆ
An automaton M (Q P, , ˆ, (q0 , p0 ), F ) will
ˆ
be constructed for L1 L2 such that
for any ( qi , p j ) Q P
ˆ((q , p ), a ) (q k , pl ) iff ( qi , a ) q k and ( p j , a) pl
i j 1 2
and
ˆ
(qi , p j ) F only if qi F1 and p j F2
18

19. We use MI to denote the automaton constructed
above for L1 L2, and so are I, FI.
w L (MI ) I( (q0,p0), w)= (qf,pf) FI qf F1
and pf F2
let w = a1a2…ak, since I( (q0,p0), w)= (qf,pf) FI ,
there exists a walk from (q0,p0) to (qf,pf) with label
w.
say (q0,p0) (qi,pj) (qr,ps) … (qf,pf) there
exists a walk from q0 to qf with label w, and there
exists a walk from p0 to pf with label w. Since qf
F1 and pf F2 w L1 L 2
19

20. Find a FA for L1 L2
from machines of L1 and L2
n n
L1 {a : n 1} {ba : n 0} and
n
L2 {b} {ba : n 2}
Use your words to explain why
ˆ
L( M ) L1 L2
20

21. Example
• If L is a regular language, prove that the
language {uv: u L, v LR} is also regular.
21

22. Regular Expressions
22

23. Regular Expressions
Regular expressions
describe regular languages
The symbol of concatenation
can by omitted, i.e. ( a + bc )*
Example: (a b c) *
describes the language
a, bc * , a, bc, aa, abc, bca,...
23

24. Recursive Definition p.72
Primitive regular expressions: , , a
Given regular expressions r and
1 r2
r1 r2 The symbol of concatenation can be
omitted, so can be written as r1 r2
r1 r2
Are regular expressions
r1 *
r1
A string is a regular expression it can be derived from
primitive r.e.’s by a finite # of applications of the rules above.
24

25. Examples
regular expression or Not regular expression:
a (X)
a* b*
a b * (c ) a* c b c
3 2 m 2 n
a ( b b )a * a ( b b )a
Precedence rules:
25

26. Languages of Regular Expressions
Lr : language of regular expression r
Example
L ( a b c) * , a, bc, aa, abc, bca,...
26

27. Definition
For primitive regular expressions:
L
L
La a
27

28. Definition (continued)
For regular expressions r and
1 r2
L r1 r2 L r1 L r2
L r1 r2 L r1 L r2
L r1 * L r1 *
L r1 L r1
28

29. Example of Language L(r)
• Regular expression r a b *
Lr L((a b)*) L(a b) *
( L(a) L(b)) *
({a} {b})* {a, b}*
29

30. Example
• Regular expression: a b a*
L a b a* L a b L a*
L a b L a*
La Lb La *
a b a *
a, b , a, aa, aaa,...
a, aa, aaa,..., b, ba, baa,...
30

31. Example
Regular expression r a b * a bb
Lr a, bb, aa, abb, ba, bbb,...
{w {a, b} : w ends with a or bb}
Find a r.e. for L={w {a,b}*: w has aa as a substring}
31

32. Example
Regular expression r aa * bb * b
2n 2m 1
Lr {a b : n, m 0}
Describe L(r) if r = (aa)*b(aa)* + a(aa)*ba(aa)*.
Find a r.e. for L={ambn: m+n is even}
Which is correct:
{a2nba2n: n 0} {a2n+1ba2n+1: n 0}; {a2nba2m:
m,n 0} {a2n+1ba2m+1: m,n 0}; {anbam:
m,n 0}
32

33. Example of L(r)
Regular expression a , ( *)*
33

34. Example
Find a regular expression for
L(r ) = { all strings with at least
two consecutive 0 }
Regular expression r (0 1) * 00 (0 1) *
Find a regular expression for
L(r ) = { all strings with exactly
two consecutive 0 }
34

35. Example
Find a regular expression for
L(r ) = { all strings without
two consecutive 0 }
Case1: no 0, i.e. 1* ; or
case2: has 0, such like(0, 01, 10, 101, 011, 110,
010,0111, 1011, 1101, 1110, 0101, 0110, 1010, 0101,…)
--0--, (1+01)*0(1+10)*
Possible answers are: 1* + (1+01)*0(1+10)*;
(1+01)*(0+ )(1+10)*; (1+01)*(0+ ); (0+ )(1+10)*;
35

36. Example
L = { all strings without two consecutive 0 }
r1 = 1* + (1+01)*0(1+10)*
r2 (1 01) * (0 )
r3 (0 )(1 10 ) *
L(r1 ) L(r2 ) L(r3 )
are equivalent
r1 , r2 r
regular expr.
(1*011*)*(0+ )+1*(0+ ) is also an equivalent r.e.
36

37. Equivalent Regular Expressions
Definition:
Regular expressions r1 r2 , i.e. they
are equivalent if L(r1) L(r2 )
Try Hw #20 on p. 77
37

38. Example
Find regular expressions for
n m
L1 {a b : n 4, m 3}
The complement of L1
38

39. Example
Find a regular expression that denotes all bit strings
whose value, with leading bit 1, when interpreted as
a binary integer, is greater than or equal to 20.
Find a r.e. r such that
L(r) = {w {0, 1}*: w = 1v and binary(w) 20}
Homework
(p.108) 2, 3, 5 ~8, 12, 13, 14, hand in: 2b, 13
(p.75) 1~21, 26~28 hand in: 6bd, 14, 16ab, 17b, 18b, 20bd,
21, 28
39

40. Regular Expressions
and
Regular Languages
40

41. Theorem
Languages
Regular
Generated by
Languages
Regular Expressions
41

42. Theorem - Part 1
Languages
Regular
Generated by
Languages
Regular Expressions
1. For any regular expression r
the language L(r ) is regular
42

43. Theorem - Part 2
Languages
Regular
Generated by
Languages
Regular Expressions
2. For any regular language L there is
a regular expression r with L( r ) L
43

44. Proof - Part 1
1. For any regular expression r
the language L(r ) is regular
Proof by induction on the size of r
44

45. Induction Basis
Primitive Regular Expressions: , , a
NFAs
L ( M1 ) L( )
regular
L( M 2 ) { } L( )
languages
a
L( M 3 ) {a} L(a )
45

46. Inductive Hypothesis
Assume for regular expressions r1 and r2 that
L(r1) and L(r2) are regular languages
We will prove:
L r1 r2
L r1 r2 Are regular
Languages
L r1 *
L r1
46

47. By definition of regular expressions:
L r1 r2 L r1 L r2
L r1 r2 L r1 L r2
L r1 * L r1 *
L r1 L r1
47

48. By inductive hypothesis we know:
L(r1) and L(r2 ) are regular languages
We also know:
Regular languages are closed under:
Union L r1 L r2
Concatenation L r L r2
1
Star L r1 *
48

49. Therefore:
L r1 r2 L r1 L r2
Are regular
L r1 r2 L r1 L r2
languages
L r1 * L r1 *
And trivially
L((r )) is a regular language
1
49

50. Example
Find an NFA for L(r) if r = (a+bb)*(ba*+ )
a a
b b b b
r = (a+bb)* a
b b
50

51. Example (Cont’d)
Find an NFA for L(r) if r = (a+bb)*(ba*+ )
a
r1 = (a+bb)*
b b
a
It is necessary!
r2 = (ba*+ ) b
51

52. Example
Find an NFA for L(r) if r = (a*b)*
Construct FAs for the expressions
( ) and a . What are the languages
that they represent?
52

53. Proof – Part 2
2. For any regular language L there is
a regular expression r with L( r ) L
Proof by construction of regular expression
53

54. Since L is regular take the
NFA M that accepts it
L( M ) L
Single final state
54

55. From M construct the equivalent
Generalized Transition Graph
in which transition labels are regular
expressions
Example:
M
a c a c
a, b a b
55

56. Another Example: b b
a
q0 q1 a, b q2
b
b b
a
q0 q1 a b q2
b
56

57. Reducing the state q1 : b b
a
q0 q1 a b q2
b
b b Add edges from qi to qj if there
was edges qi to qj via q1, i, j 1:
a
q0 q1 a b q2 q0 to q0 via q1:
q0 to q2 via q1:
q2 to q0 via q1:
b
bb * a q2 to q2 via q1:
b
q0 bb * (a b) q2
57

58. Resulting Regular Expression:
bb* a b
q0 bb * (a b) q2
r (bb * a ) * bb * (a b)b *
L(r ) L( M ) L
58

59. In General
For any transition graph satisfying
q0 F and | F = {qf} | = 1
then for any state q , q q0 , q qf
will be removed.
59

60. a d
Removing state q :
c
q1 q2
Add edges from qi to qj if b
there were edges qi to qj via q:
e f h i
q
g
60

61. a
a d
d
Removing state q :
c
q1 q2
b
e f h i
q1 to q1 via q:
q
g
a +eg*f d
c
q1 q2
b 61

62. a d
Removing state q : c
q1 q2
b
e f h i
q1 to q1 via q:
to q2 via q: q
g
a+eg*f d
c
q1 q2
b+eg*i 62

63. a d
Removing state q :
c
q1 q2
b
e f h i
q1 to q1 via q:
to q2 via q: q
q2 to q1 via q:
g
a+eg*f d
c+hg*f
q1 q2
b+eg*i 63

64. a d
Removing state q :
c
q1 q2
b
e f h i
q1 to q1 via q:
to q2 via q: q
q2 to q1 via q:
to q2 via q: g
a+eg*f d+hg*i
c+hg*f
q1 q2
b+eg*i 64

65. The final transition graph:
r4
q0 qf
r2
The resulting regular expression:
r r2 r4 *
L(r ) L( M ) L
65

66. The final transition graph:
r4
r3
q0 qf
r2
The resulting regular expression:
r r2 (r4 r3r2 ) *
L(r ) L( M ) L
66

67. The final transition graph:
r1 r4
r3
q0 qf
r2
The resulting regular expression:
r r1 * r2 (r4 r3r1 * r2 ) *
L(r ) L( M ) L
67

68. Removing state q :
e
c
if qi q qj
a b
e
d c
if qi q qj
a
68

69. Removing state q : e
f q g
d c
Add edges from qi to qj if there a b
were edges qi to qj via q: q1 h q2
i
r1 r4 j k
l m n o
r2
q1 q2
r3 q3
r5 q1 to q1 via q: p
r6 r7 r8
to q2 via q:
q3 to q3 via q: q3 to q1 via q:
q2 to q1 via q: to q2 via q:
r9 to q2 via q: to q3 via q:
to q3 via q:
69

70. Last Words about
Conversion from NFA to Reg. Exp.
• Remove any inaccessible states (from q0).
• If the initial state is also a final state…
• If there is more than one final states…
Hw for 3.2 (p.87): 1 ~13, 18.
70

71. L is regular
a reg. exp. r L=L(r)
a FA M L=L(M)
Show L is regular by finding its regular
expression:
L = {w {a,b}*: na(w) is even, nb(w) is odd}
It is difficult to find its reg. exp. directly.
Use FA with states:
eo representing so far it has even # of as and
odd # of bs being read, etc..
71

72. Closure Properties of
Regular Languages
Remaining material of
Section 4.1
72

73. Closure Properties
• Closure Properties of Regular Languages
– Closure under Simple Set Operations
• union, intersection, concatenation,
complementary, star-closure, reversal
– Closure under Other Operations
• Homomorphism (Def. 4.1, p.103) skip
• Right Quotient (Def. 4.2, p. 104)
73

74. Right Quotient L1/ L2
• The right quotient of L1 with L2 is
L1/L2 = {x: xy L1 for some y L2}
L1={ab, abb, abbb}, L2 ={bman: m > n}
L1 / L2 = ?
Thm 4.4 (p.106) The family of regular languages
is closed under right quotient with a regular
language.
74

75. Right Quotient L1/ L2
• The right quotient of L1 with L2 is
L1/L2 = {x: xy L1 for some y L2}
Let L1=L(a*baa*) and L2 =L (ab* )
Find L1/L2 & L2/L1
Thm 4.3 (p.104) & 4.4 (p.106) The family of regular
languages is closed under arbitrary
homomorphisms and right quotient with a
regular language. 75

76. Right quotient example (p.109, Hw #11)
• Give an example of L1 & L2 such that
L1 = L1L2/L2.
• Give an example to show that
L1 = L1L2/L2 is not true.
Do hw (p.109) : 10, 11, 15 of your own.
76