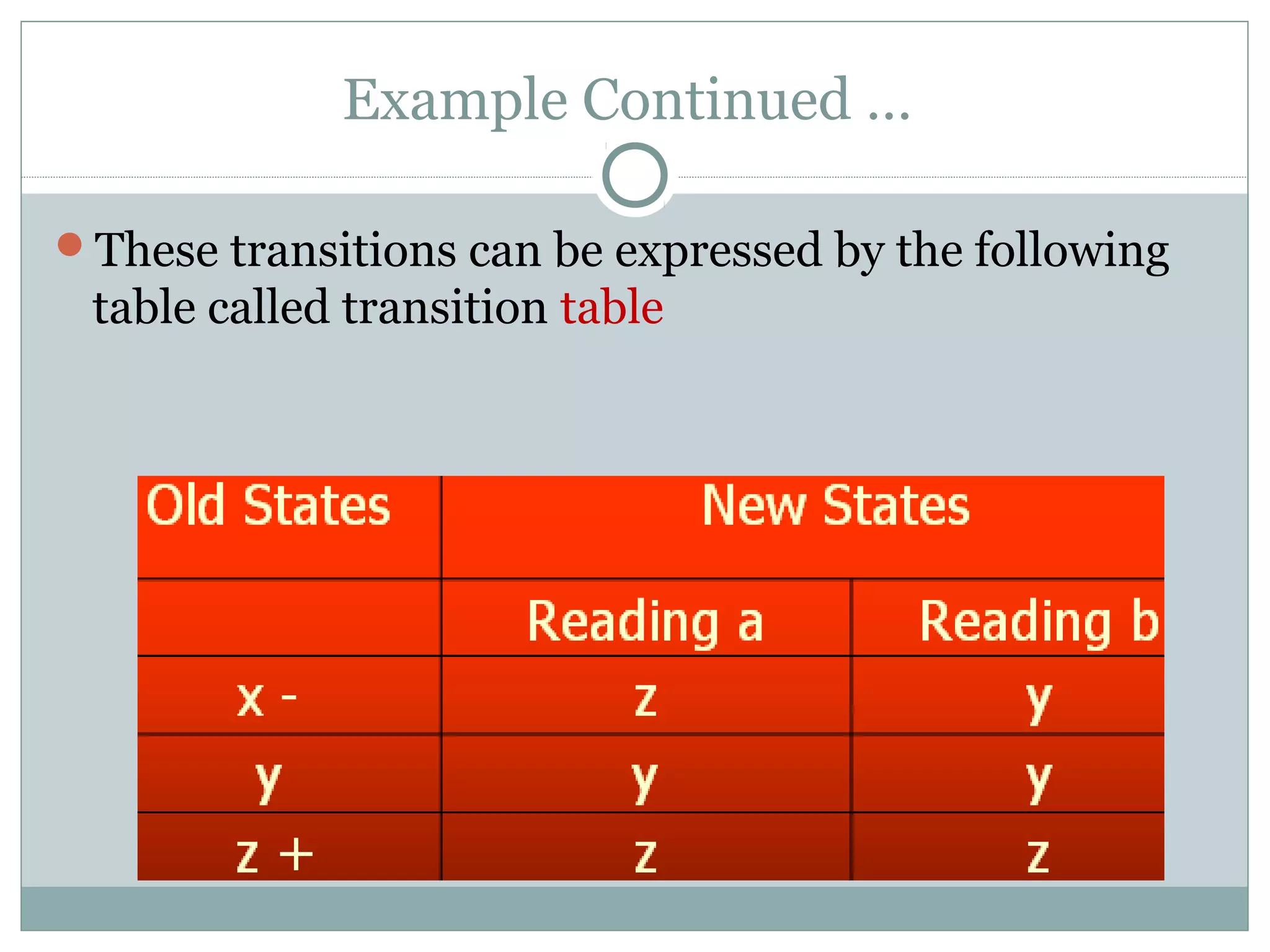
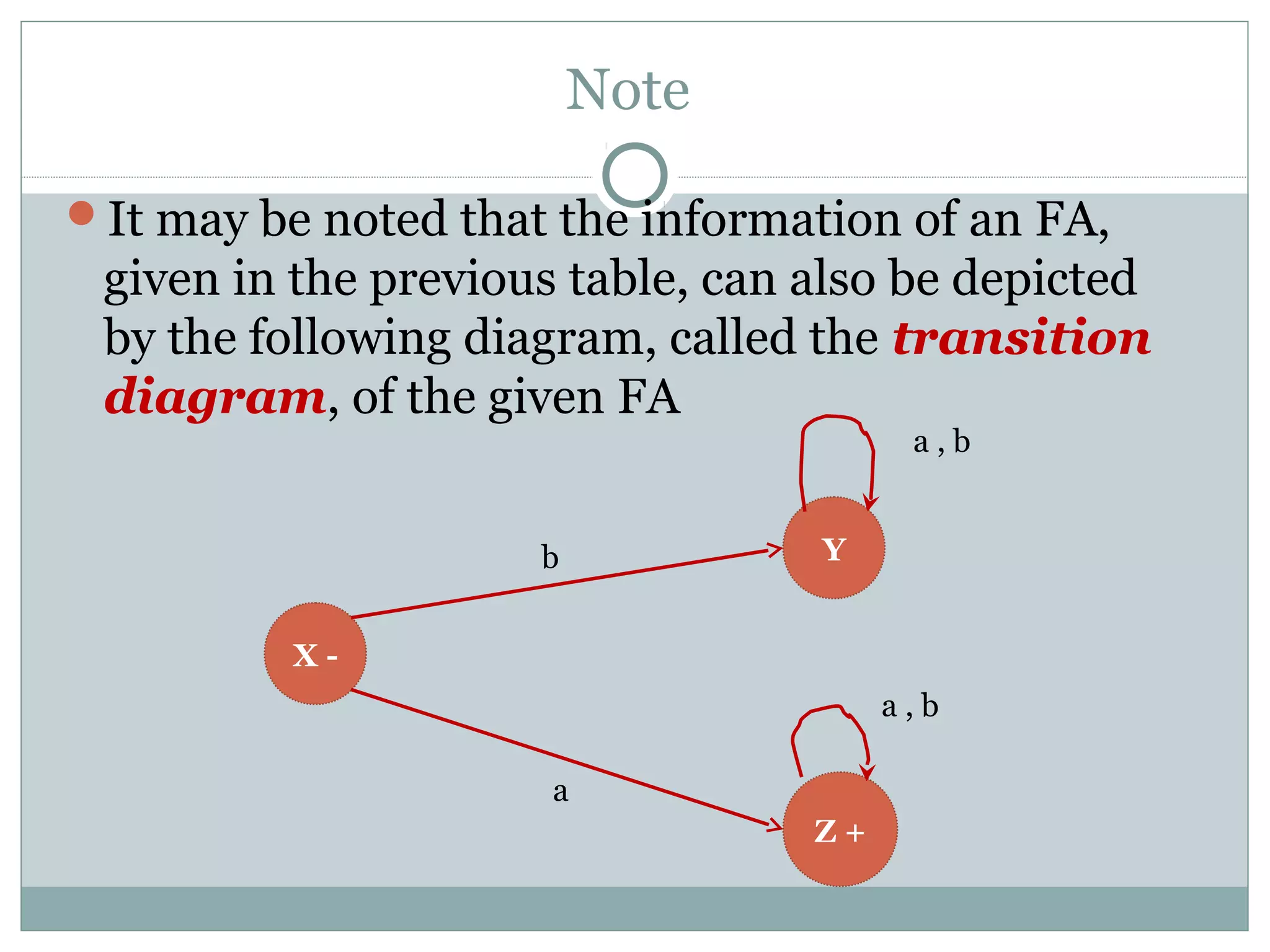
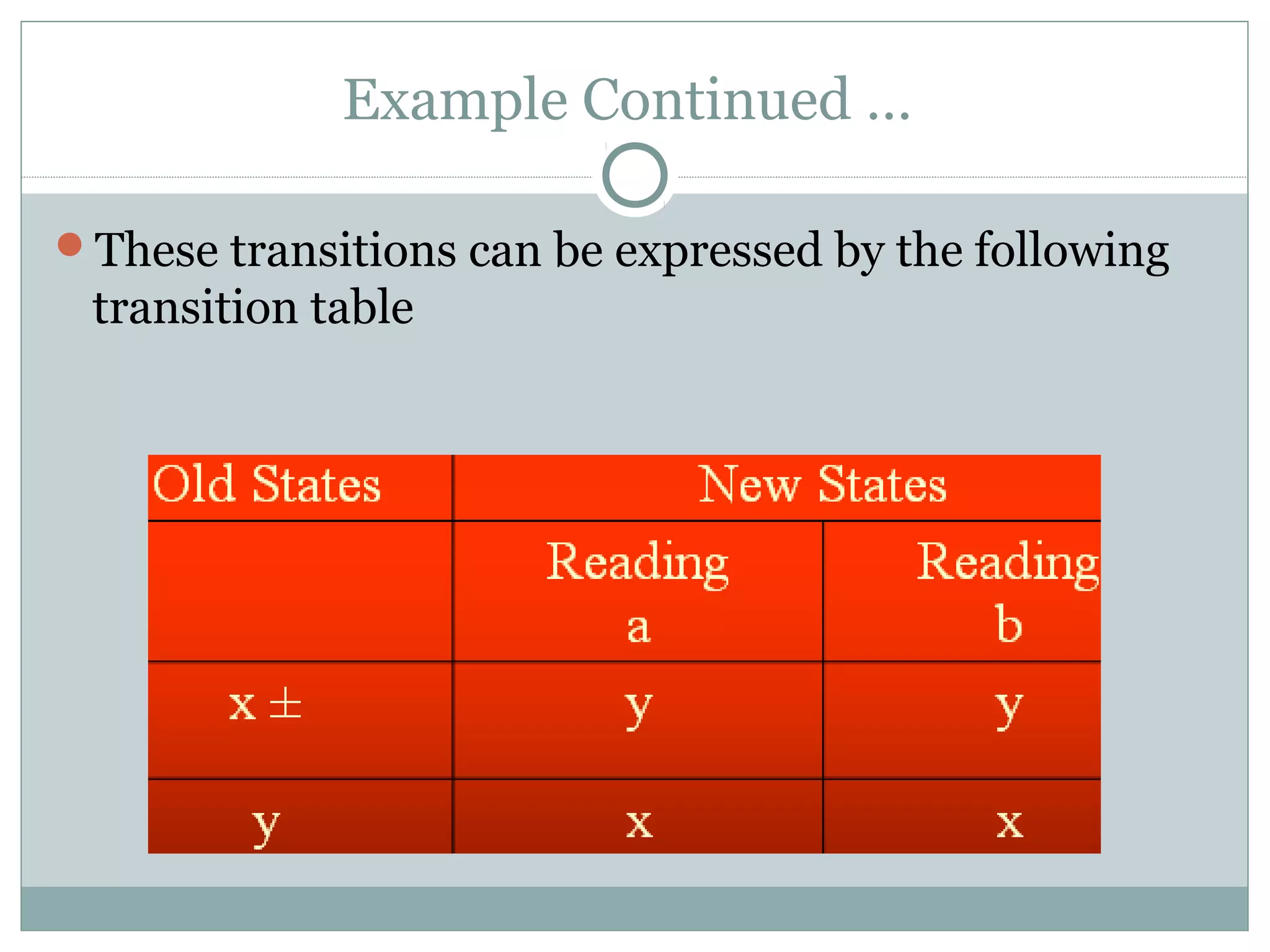
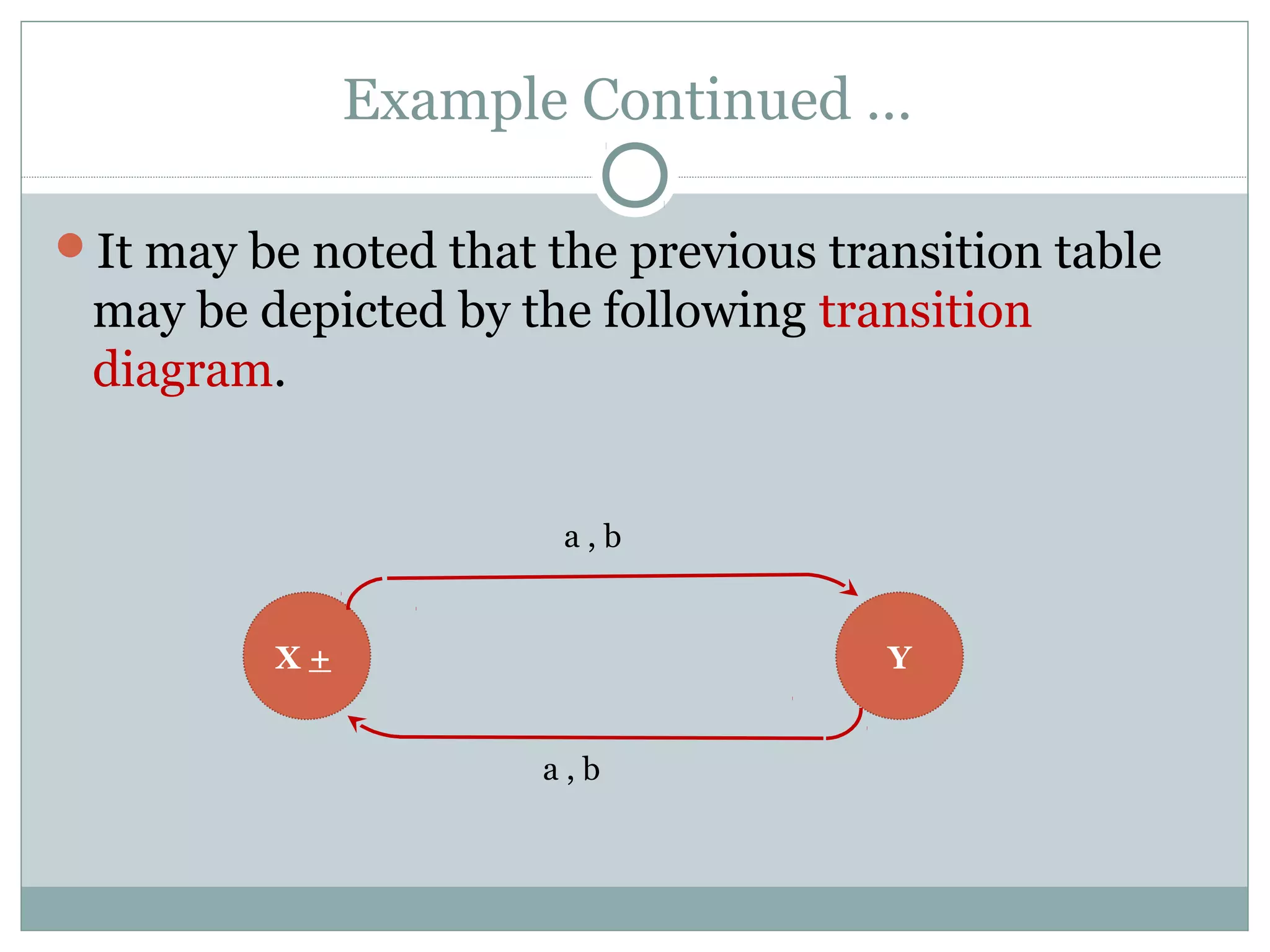
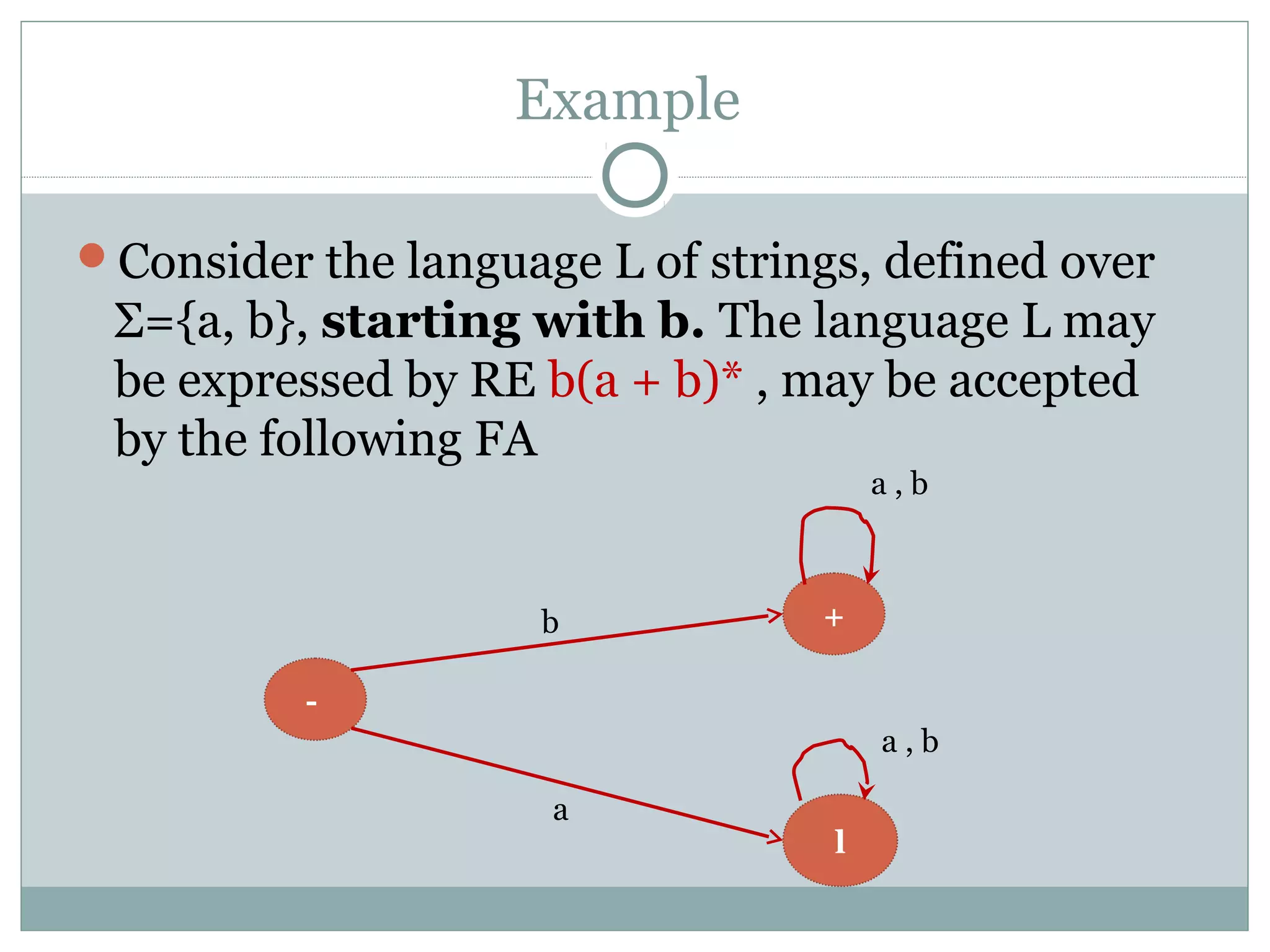
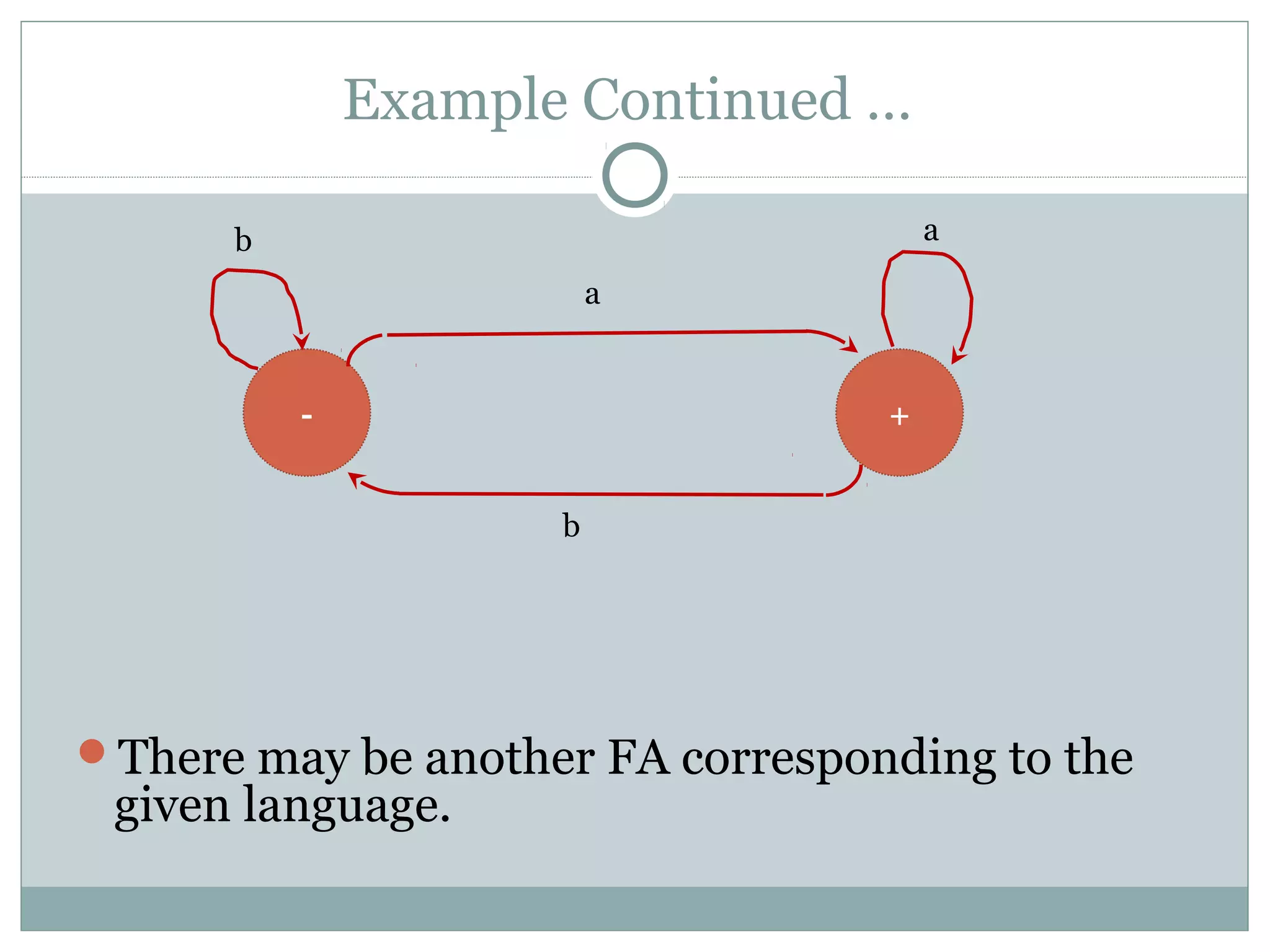
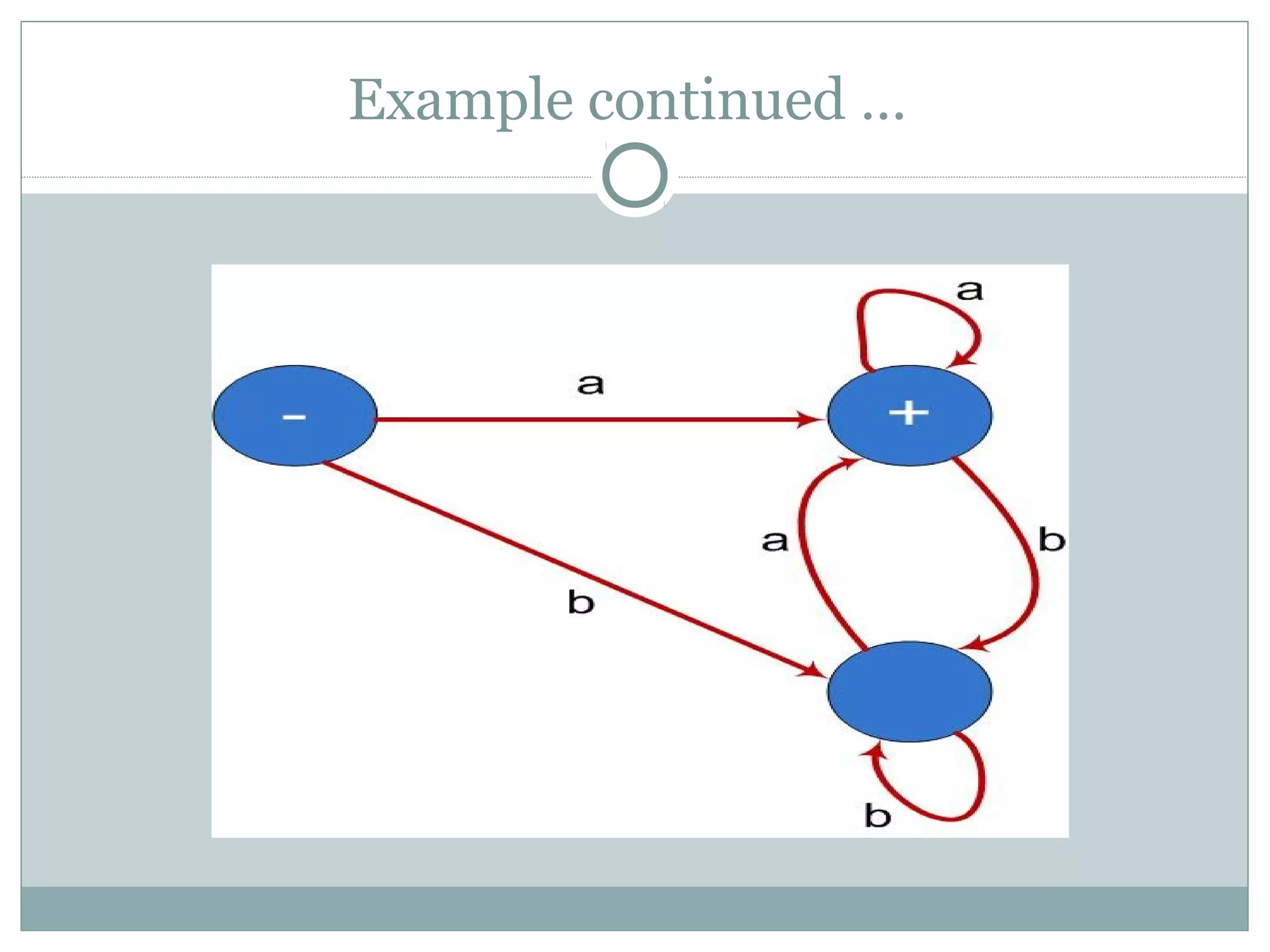
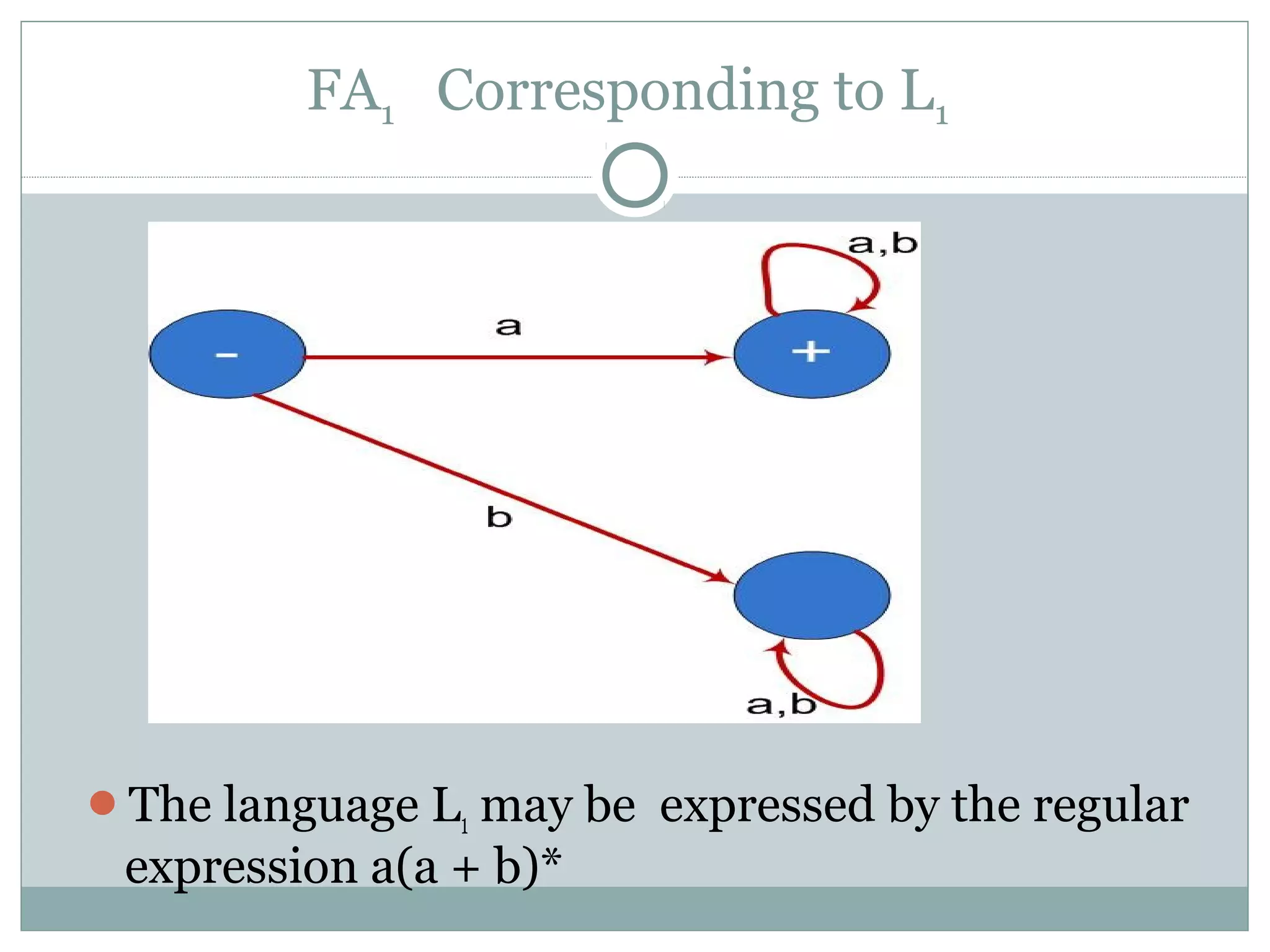
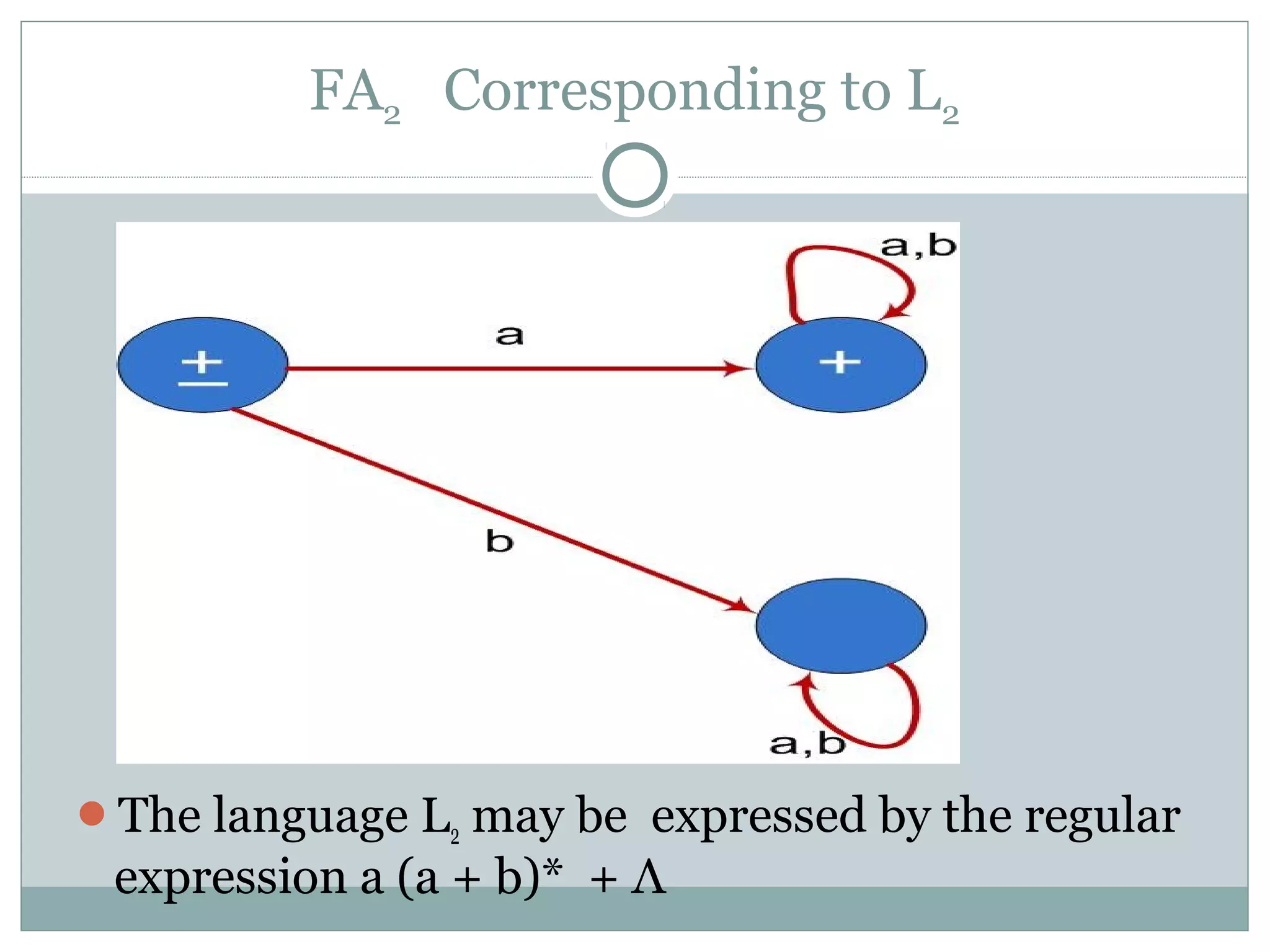
This document discusses finite automata and regular languages. It defines a finite automaton as having a finite number of states, with one initial and some final states, a finite input alphabet, and transitions between states based on input letters. Examples of finite automata are given to accept languages of strings of odd length, starting with b, and ending in a. It notes that a language can have multiple accepting finite automata, but an automaton only accepts one language. The relationship between regular expressions and finite automata is also discussed.