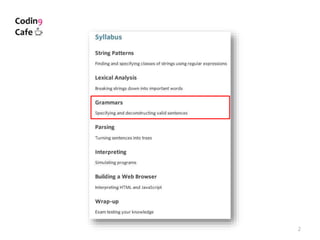
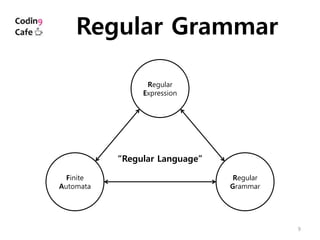
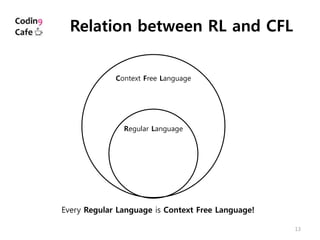
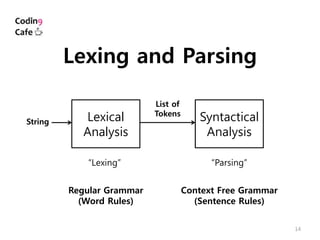
The document discusses different types of programming languages grammars including regular grammars, context-free grammars, and context-sensitive grammars. It provides examples of regular expressions and grammars to generate specific string languages. While all regular languages are context-free, not all context-free languages are regular. Lexical analysis uses regular grammars to tokenize input strings, while parsing uses context-free grammars to analyze sentence structure.

1. Programming Languages
Building a Web Brower
Instructor : Westley Weimer
1

2. 2

3. 3
Grammar
how words and their component parts combine to form sentences
I think (O)
Sentence → Subject Verb
think think I (X)
exp → num + num
7 + 5 (O)
+ 2 5 (X)

4. 4
Grammar
G = ( VN, VT, P, S )
VN = A finite set of non-terminal symbols
VT = A finite set of terminal symbols
P = A finite set of production rules
S = S∈N, start symbol

5. 5
Grammar
S ⇒ aA (S → aA)
S ⇒ abS (A → bS)
S ⇒ abbB (S → bB)
S ⇒ abbaS (B → aS)
S ⇒ abba (S → E)
P : S → aA | bB | Epsilon
P : A → bS
P : B → aS
G = ({S, A}, {a, b}, P, S)
VN VT

6. 6
Grammar
 Unrestricted Grammar
 Context-Sensitive Grammar
 Context-Free Grammar
 Regular Grammar

7. 7
Regular Grammar
RLG(Right-Linear Grammar) : A → tB, A → t
OR
LLG(Left-Linear Grammar) : A → Bt, A → t
P : S → aA
P : A → bA | b
P : S → Aa
P : A → Ab | b

8. 8
Regular Grammar
P : S → aA | c
P : A → Sb
G = ({S, A}, {a, b, c}, P, S)
S ⇒ aA ⇒ aSb ⇒ acb
S ⇒ aA ⇒ aSb ⇒ aaAb
S ⇒ aaSbb ⇒ aacbb
L(G) = { ancbn | n ≥ 0 }
↔ r"a*cb*" (X)
P : S → aA | c
P : A → bS
G = ({S, A}, {a, b, c}, P, S)
S ⇒ aA ⇒ abS ⇒ abc
S ⇒ aA ⇒ abS ⇒ abaA
S ⇒ ababS ⇒ ababc
L(G) = { (ab)n c | n ≥ 0 }
↔ r "(?:ab)*c" (O)

9. 9
Regular Grammar
Regular
Expression
Finite
Automata
Regular
Grammar
“Regular Language”

10. 10
Context Free Grammar
doesn't care about the line above or below it
X = 1
X + 2 → 3
X = 3
X + 2 → 5
X + 2

11. 11
Context Free Grammar
P : A → α
V*
P : S → aA | c
P : A → Sb
V* = ( VN U VT )*, A string of variables and/or terminals

12. 12
Context Free Grammar
P : S → ( S )
P : S → EpsilonP :
G = ({S}, {( , )}, P, S)
S ⇒ ( S ) ⇒ ( )
S ⇒ ( S ) ⇒ (( S )) ⇒ (( ))
S ⇒ ( S ) ⇒ (( S )) ⇒ ((( S ))) ⇒ ((( )))
L(G) = { (n )n | n ≥ 1 } ↔ r"(*)*" (X)

13. 13
Relation between RL and CFL
Context Free Language
Regular Language
Every Regular Language is Context Free Language!

14. 14
Syntactical
Analysis
Lexical
Analysis
“Lexing” “Parsing”
Regular Grammar
(Word Rules)
Context Free Grammar
(Sentence Rules)
String
List of
Tokens
Lexing and Parsing

15. 15