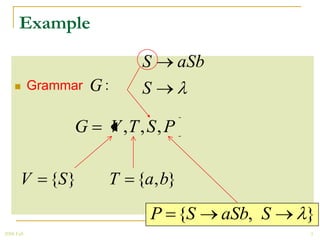
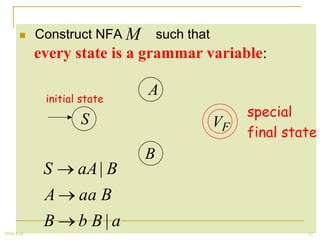
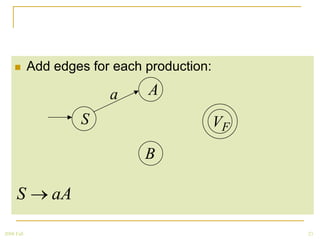
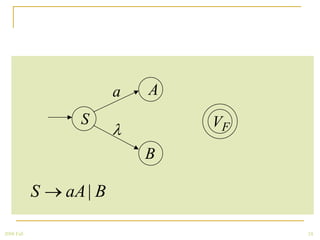
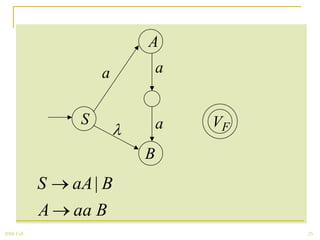
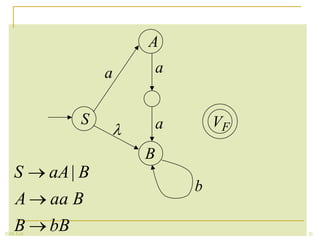
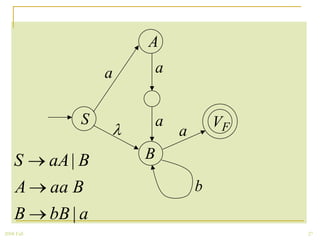
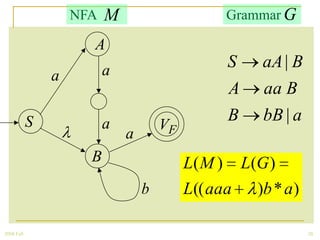
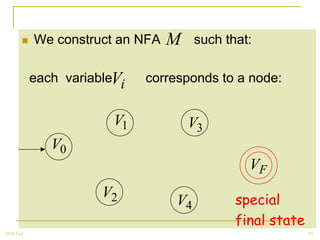
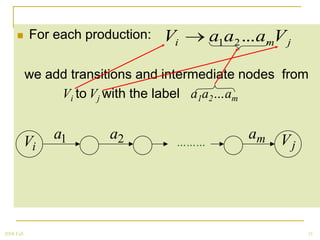
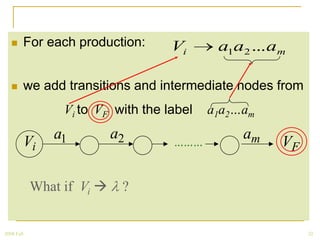
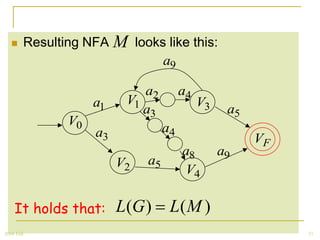
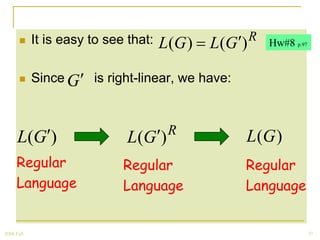
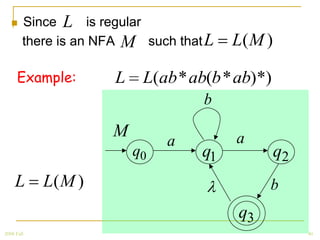
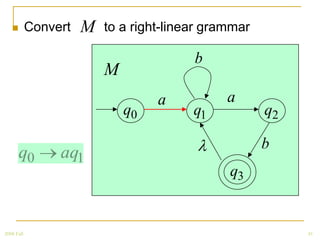
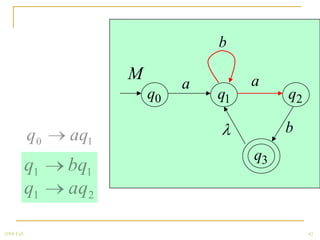
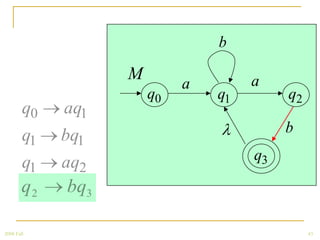
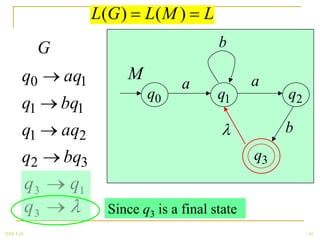
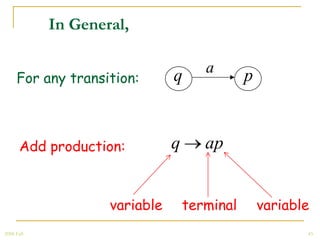
The document discusses regular grammars and how they generate regular languages. It defines regular grammars as grammars that are either right-linear or left-linear, meaning productions have at most one variable on the right-hand side. It then proves that languages generated by regular grammars are regular by constructing a finite automaton from a regular grammar that accepts the same language. Specifically, it shows how to build an NFA where states correspond to variables in the grammar and transitions correspond to grammar productions.

1. 3.3 Grammars
HW on p.97 : 1~13, 17, 26(p.111)
2008 Fall 1

2. Recall Notation
 Grammar G V ,T , S , P p.21
V : Set of variables
T : Set of terminal symbols
S : Start variable
P: Set of Production rules
2008 Fall 2

3. Example
S aSb
 Grammar G: S
G V ,T , S , P
V {S } T {a, b}
P {S aSb, S }
2008 Fall 3

4. More Notation on Derivations
 Sentential Form:
A sentence that contains variables
 Example:
A derivation from the starting variable
S aSb aaSbb aaaSbbb aaabbb
Sentential Forms sentence
2008 Fall 4

5. *
 We write: S aaabbb
Instead of:
S aSb aaSbb aaaSbbb aaabbb
2008 Fall 5

6. Linear Grammars
2008 Fall 6

7. Linear Grammars
 Grammars with productions of the form
X Y with X V, Y V T*, and
Y has at most one variable from V
i.e. at most one variable at the right side of a production
Examples:
S Ab
S aSb |
A aAb |
2008 Fall 7

8. A Non-Linear Grammar
2 variables on the right
 Grammar G : S SS of the production
S
S aSb
S bSa
L(G) {w : na ( w) nb ( w)}
Number of a in string w
2008 Fall 8

9. Right-Linear Grammars
 All productions A xB
have form:
or
Example:
A x
S abS
x : string of terminals
S a including
2008 Fall 9

10. Left-Linear Grammars
All productions have form: A Bx
or
Example:
A x
S Aab
A Aab | B
x : string of terminals
B a including
2008 Fall 10

11. Regular Grammars
2008 Fall 11

12. Regular Grammars
 A regular grammar is any
right-linear or left-linear grammar
 Examples:
G1 G2
S abS S Aab
S a A Aab | B
B a
2008 Fall 12

13. Observation-1
 Regular grammars generate regular languages
 Examples: G2
G1 S Aab
A Aab | B
S abS
B a
S a
2008 Fall 13

14. Observation-2
S abS
G1
S a
Consider string w = abababa:
S abS ababS abababS abababa
a The derivation S * abababa
S b
corresponds to a walk in a FA with label
a
abababa from the state S to a final state.
2008 Fall 14

15. Regular Grammars
Generate
Regular Languages
2008 Fall 15

16. Theorem
Languages
Regular
Generated by
Languages
Regular Grammars
2008 Fall 16

17. Theorem - Part 1
Languages
Regular
Generated by
Languages
Regular Grammars
Any regular grammar generates
a regular language
G: regular grammar, show L(G) is regular
2008 Fall 17

18. Theorem - Part 2
Languages
Regular
Generated by
Languages
Regular Grammars
Any regular language is generated
by some regular grammar
L is regular, show there is a regular
grammar G such that L= L(G).
2008 Fall 18

19. Proof – Part 1
Languages
Regular
Generated by
Languages
Regular Grammars
The language L (G ) is regular if G is
any regular grammar
2008 Fall 19

20. The case of Right-Linear Grammars
 Let G be a right-linear grammar
We will prove: L(G ) is regular
Proof idea:
We will construct NFA M
with L( M ) L(G )
2008 Fall 20

21.  Grammar G is right-linear
Example: S aA | B
A aa B
B b B|a
Note that
V= {S, A, B} in the given regular grammar
2008 Fall 21

22.  Construct NFA M such that
every state is a grammar variable:
initial state
A
special
S VF
final state
B
S aA | B
A aa B
B b B|a
2008 Fall 22

23.  Add edges for each production:
a A
S VF
B
S aA
2008 Fall 23

24. a A
S VF
B
S aA | B
2008 Fall 24

25. A
a a
S a VF
B
S aA | B
A aa B
2008 Fall 25

26. A
a a
S a VF
B
S aA | B
b
A aa B
B
2008 Fall
bB 26

27. A
a a
S a VF
a
S aA | B B
A aa B b
B bB | a
2008 Fall 27

28. NFA M Grammar G
A
a S aA | B
a
A aa B
S a B bB | a
VF
a
B L( M ) L(G )
b L(( aaa )b * a )
2008 Fall 28

29. In General
 A right-linear grammar G
has variables:V0 ,V1,V2 ,
and productions:
Vi a1a2 ...amV j
or
Vi a1a2 ...am
2008 Fall 29

30.  We construct an NFA M such that:
each variableVi corresponds to a node:
V1 V3
V0
VF
V2 special
V4
final state
2008 Fall 30

31.  For each production: Vi a1a2 ...amV j
we add transitions and intermediate nodes from
Vi to Vj with the label a1a2…am
Vi a1 a2 ………
am V
j
2008 Fall 31

32.  For each production: Vi a1a2 ... am
 we add transitions and intermediate nodes from
Vi to VF with the label a1a2…am
a1 a2 ………
am
Vi VF
What if Vi  ?
2008 Fall 32

33.  Resulting NFA M looks like this:
a9
a2 a4
a1 V1 V3
a3 a5
V0
a3 a4
VF
a8 a9
V2 a5
V4
It holds that: L(G ) L( M )
2008 Fall 33

34. The case of Left-Linear Grammars
 Let G be a left-linear grammar
 We will prove: L(G ) is regular
Proof idea:
We will construct a right-linear
grammar G with
R
L(G ) L(G )
2008 Fall 34

35. 
Since G is left-linear grammar
the productions look like:
A Ba1a2 ... ak
A a1a2 ... ak
2008 Fall 35

36.  Construct right-linear grammar G from G by
G:X Y G' : X YR
( Bv )R = vR BR = vR B
Left linear G Right linear G
A → Bv A R
v B
A Ba1a2 ... ak A ak ... a2 a1 B
A v R
A v
A a1a2 ... ak A ak ... a2 a1
2008 Fall 36

37.  It is easy to see that: R
L(G ) L(G ) Hw#8 p.97
 Since G is right-linear, we have:
R L(G )
L(G ) L(G )
Regular Regular Regular
Language Language Language
2008 Fall 37

38. Proof - Part 2
Languages
Regular
Generated by
Languages
Regular Grammars
Any regular language L is generated
by some regular grammar G
2008 Fall 38

39. Any regular language L is generated
by some regular grammar G
Proof idea:
Let M be the NFA with L L(M ).
Construct from M a regular grammar G
such that L ( M ) L (G )
2008 Fall 39

40.  Since L is regular
there is an NFA M such that L L(M )
Example: L L(ab * ab(b * ab)*)
b
M a
a
q0 q1 q2
L L(M ) b
q3
2008 Fall 40

41.  Convert M to a right-linear grammar
b
M
a a
q0 q1 q2
b
q0 aq1
q3
2008 Fall 41

42. b
M a
a
q0 q1 q2
q0 aq1 b
q3
q1 bq1
q1 aq2
2008 Fall 42

43. b
M a
a
q0 q1 q2
q0 aq1
b
q1 bq1
q1 aq2 q3
q2 bq3
2008 Fall 43

44. L(G ) L( M ) L
G b
q0 aq1 M a
a
q0 q1 q2
q1 bq1
q1 aq2 b
q2 bq3 q3
q3 q1
q3 Since q3 is a final state
2008 Fall 44

45. In General, Converting given FA into a
regular grammar:
a
For any transition: q p
Add production: q ap
variable terminal variable
2008 Fall 45

46. For any final state: qf
Add production: qf
2008 Fall 46

47.  Since G is right-linear grammar
G is also a regular grammar
with L(G ) L( M ) L
2008 Fall 47

48. Construct a left-linear grammar
from FA: hw# 9 p.97
 If L={strings with abb as prefix}
From FA of the reverse of L, LR, we can
easily obtain a right linear grammar for LR.
Finally, convert this grammar into a left-
linear one for L.
2008 Fall 48

49. Example
 Sometimes we can construct a regular grammar
by inspecting the corresponding regular
expression.
Example: Find both a left-linear and right-
linear grammar for L(aab*a)?
L(aab*a)* ?
L((ab+a)b*a) ?
L(aa*(ab+a)*)?
2008 Fall 49

50. Example
 Consider language L = { anbm : n+m is even}
Find its right-, left-linear grammar by
(1) inspection from reg. exp. (2) FA.
We have so far introduce three ways to represent a
regular language: Finite State Machine, Regular
Expression, Regular Grammar.
2008 Fall 50