This document summarizes a lecture on context free languages and grammars. It includes: - Definitions of context free grammars and languages. A context free grammar is defined as a 4-tuple (V, Σ, R, S) where V is variables, Σ is terminals, R is rules, and S is the start variable. - Examples of context free grammars that generate specific languages. Grammars are provided to generate languages of even length palindromes, strings with a^i b^j where i,j > 0, and strings with a^i b^2i. 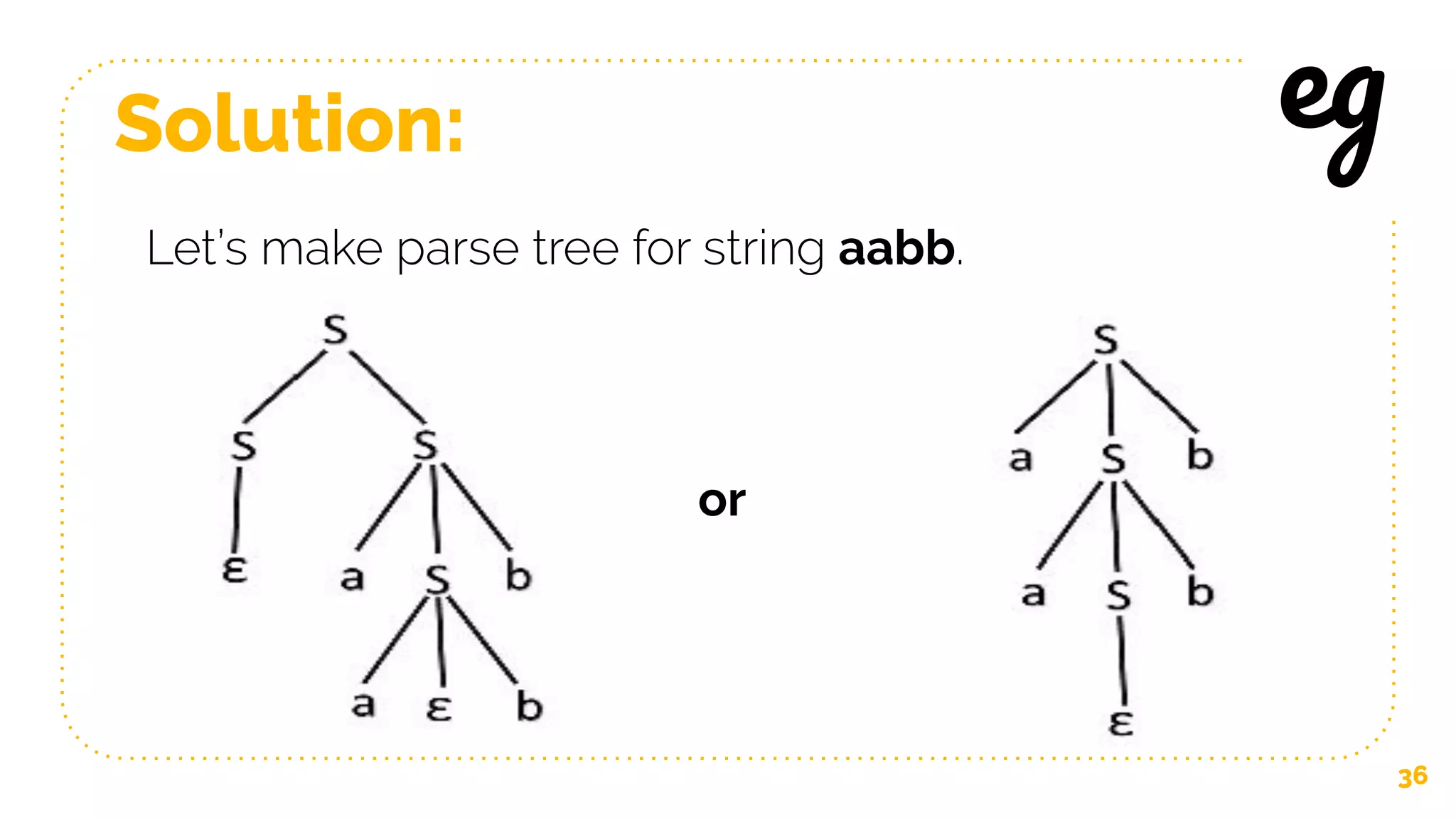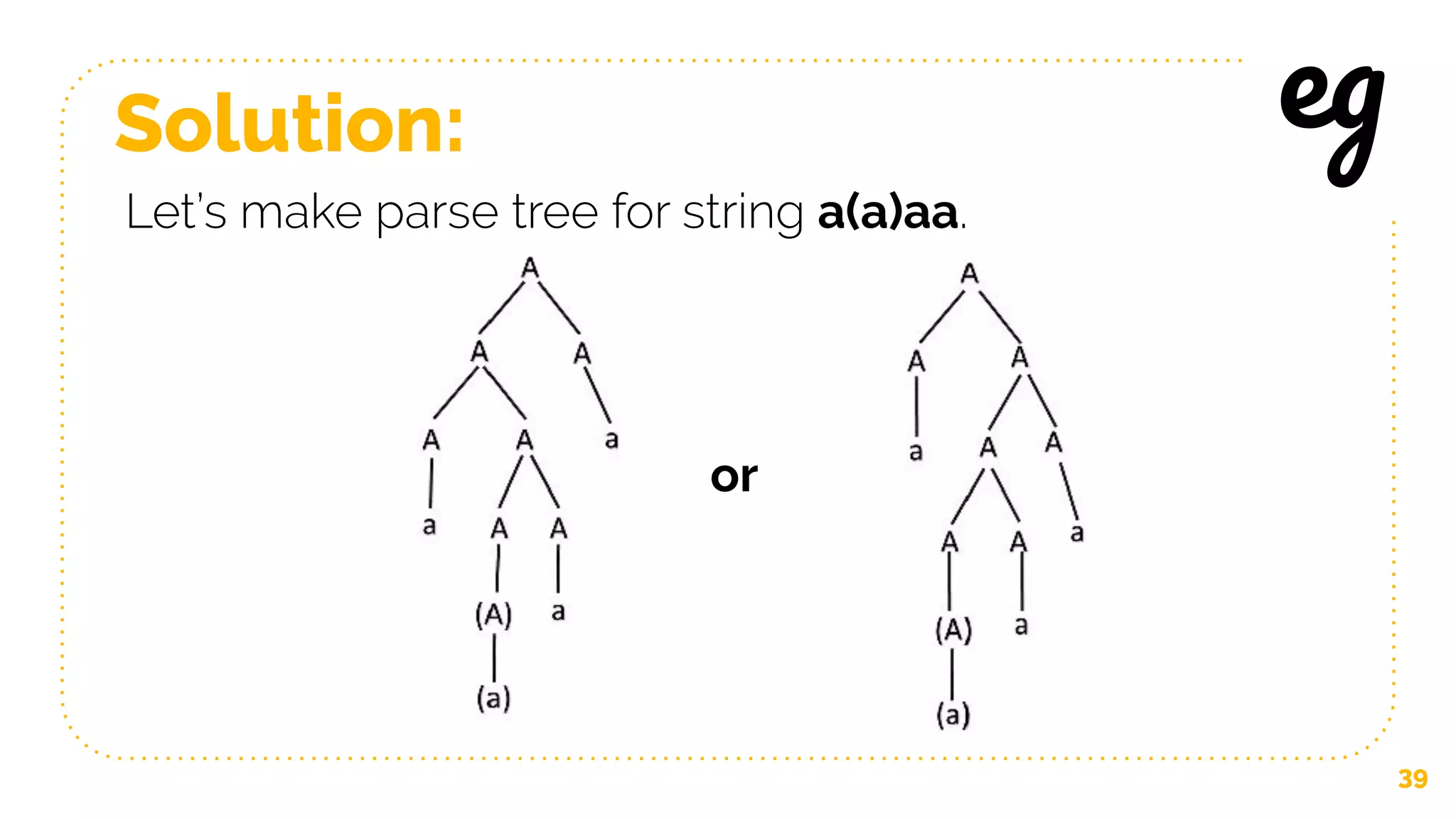- Discussion of ambiguity in grammars and languages. A grammar is ambiguous if it can derive

1. Lecture-17
Context Free Languages
Group ID - 11
Prepared under CS222 at IIT Jodhpur

2. Contribution
Each person has contributed almost equally for this
presentation.
Whereas specific contributions include
Muskan Bathla(B18CSE036): slides 27-50=24 slides
*Nivedit Jain(B18CSE039): slides 3-18, slide 51- 62=28 slides
Sanskar Mani(B18CSE048): slides 19-26=8 slides
* was on academic leave during lecture. Approval
2

3. Presentation Outline
3
Slide 4-18
Context Free
Language
Introduction
and Grammar
(Prerequisite)
Slide 19-21
Writing
Grammar for
Languages
Slide 22-31
Examples
and Problems
Slide 43-61
Chomsky
Normal Form
Slide 32-42
Ambiguous
Grammar

4. Context Free
Language

5. The collections of languages associated with context-free
grammars are called the Context Free Languages.
5

6. The collections of languages associated with context-free
grammars are called the Context Free Languages.
6
Context Free Grammars ???

7. The collections of languages associated with context-free
grammars are called the Context Free Languages.
7
Context Free Grammars ???

8. Context Free
Grammar ?
8

9. Context Free Grammar
9
Formally,
A context-free grammar is a 4-tuple (V,∑,R,S), where
1. V is a finite set called the variables.
2. ∑ is a finite set, disjoint from V, called terminals.
3. R is a finite set of rules, with each rule being a
variable and a string of variables and terminals, and
4. S ϵ V is the start variable
Michael Sipser. 1996. Introduction to the Theory of Computation (1st. ed.). International Thomson Publishing.

10. Context Free Grammar
10
Formally,
A context-free grammar is a 4-tuple (V,∑,R,S), where
1. V is a finite set called the variables.
2. ∑ is a finite set, disjoint from V, called terminals.
3. R is a finite set of rules, with each rule being a
variable and a string of variables and terminals, and
4. S ϵ V is the start variable
Michael Sipser. 1996. Introduction to the Theory of Computation (1st. ed.). International Thomson Publishing.

11. Context Free Grammar
11
Formally,
A context-free grammar is a 4-tuple (V,∑,R,S), where
1. V is a finite set called the variables.
2. ∑ is a finite set, disjoint from V, called terminals.
3. R is a finite set of rules, with each rule being a
variable and a string of variables and terminals, and
4. S ϵ V is the start variable
Michael Sipser. 1996. Introduction to the Theory of Computation (1st. ed.). International Thomson Publishing.
SURE!!

12. Let's consider an example
12
eg
A → 0A1
A → B
B → #

13. Let's consider an example
13
eg
A → 0A1
A → B
B → #
A grammar
consists of a
collection of
substitution
rules, also called
productions.

14. Let's consider an example
14
eg
A → 0A1
A → B
B → #
Symbol is called
a variable

15. Let's consider an example
15
eg
A → 0A1
A → B
B → #
The string
consists of
variables and
other symbols
called terminals

16. Let's consider an example
16
eg
A → 0A1
A → B
B → #
Start variable, it
occurs on the
left-hand side of
the topmost rule.
I am A and I am
the start variable

17. Context Free Grammar
17
Formally,
A context-free grammar is a 4-tuple (V,∑,R,S), where
1. V is a finite set called the variables.
2. ∑ is a finite set, disjoint from V, called terminals.
3. R is a finite set of rules, with each rule being a
variable and a string of variables and terminals, and
4. S ϵ V is the start variable
Michael Sipser. 1996. Introduction to the Theory of Computation (1st. ed.). International Thomson Publishing.

18. Context Free Grammar
18
Formally,
A context-free grammar is a 4-tuple (V,∑,R,S), where
1. V is a finite set called the variables.
2. ∑ is a finite set, disjoint from V, called terminals.
3. R is a finite set of rules, with each rule being a
variable and a string of variables and terminals, and
4. S ϵ V is the start variable
Michael Sipser. 1996. Introduction to the Theory of Computation (1st. ed.). International Thomson Publishing.

19. Grammar for
Languages

20. Method
20
You use a grammar to describe a language by
generating each string of that
language in the following manner -
1. Write down the start variable. It is the variable on
the left-hand side of the
top rule, unless specified otherwise.

21. Method (contd.)
21
2. Find a variable that is written down and a rule
that starts with that variable.
Replace the written down variable with the
right-hand side of that rule.
3. Repeat step 2 until no variables remain.

22. Examples

23. Example 1
23
eg
Write grammar for all
even length palindromes.

24. Solution:
24
eg
Even length palindromes =
{aa , bb , aaaa , abba , baab ,
bbbb , … }
S→aSa | bSb | aa | bb

25. Example 2
25
eg
Write grammar to
generate
L = { ai
bj
| i,j > 0 }

26. Solution:
26
eg
L = {ab , aab , abb , aaab ,
aabb , abbb , bbbb , … }
S→AB
A→aAa | a
B→bBb | b

27. Example 3
27
eg
Write grammar to
generate
L = { ai
b2i
| i,j > 0 }

28. Solution:
28
eg
L = { ε, abb, aabbbb, … }
S→ASB | ε
A→a
B→bb

29. Example 4
29
eg
E → E+E | ExE | (E) | a
w= a+axa
Write the parse tree for w.

30. Solution:
30
eg
or

31. Solution (contd.) :
31
eg
● As we can see, there are two different parse
trees possible
● When a grammar generates the same string in
different ways, we say that the string is derived
ambiguously
● Such a grammar is known as ambiguous
grammar
Michael Sipser. 1996. Introduction to the Theory of Computation (1st. ed.). International Thomson Publishing.

32. Ambiguity

33. Ambiguous Grammar
33
Formally,
A string w is derived ambiguously in context-free
grammar G if it has two or more different leftmost
derivations. Grammar G is ambiguous if it
generates some string ambiguously.
Michael Sipser. 1996. Introduction to the Theory of Computation (1st. ed.). International Thomson Publishing.

34. Note Points:
34
1. When we say that a grammar generates a string
ambiguously, we mean that the string has two
different parse trees, not two different derivations.
2. Sometimes, we can find an unambiguous
grammar that generates the same language as
generated by our ambiguous grammar.
Michael Sipser. 1996. Introduction to the Theory of Computation (1st. ed.). International Thomson Publishing.

35. Example 1
35
eg
S → aSb | SS | ε
Check if the grammar is
ambiguous or not.

36. Solution:
36
eg
Let’s make parse tree for string aabb.
or

37. Solution (contd.) :
37
eg
Since two different parse trees are
possible, the language is ambiguous.

38. Example 2
38
eg
A → AA | (A) | a
Check if the grammar is
ambiguous or not.

39. Solution:
39
eg
Let’s make parse tree for string a(a)aa.
or

40. Solution (contd.) :
40
eg
Since two different parse trees are
possible, the language is ambiguous.

41. Inherently Ambiguous Language
41
Some languages can be generated only by
ambiguous grammars.
Such languages are called inherently ambiguous.
Michael Sipser. 1996. Introduction to the Theory of Computation (1st. ed.). International Thomson Publishing.

42. Example
42
eg
A= { ai
bj
ck
| i=j or j=k }
A is inherently ambiguous

43. Chomsky Normal
Form

44. Chomsky Normal Form
44
Formally,
A context-free grammar is in chomsky normal form if every rule is
of the form
A→BC
A→a
where a is any terminal and A,B and C are any variable except that
B and C may not be start variable. In addition we permit the rule
S→ε
Michael Sipser. 1996. Introduction to the Theory of Computation (1st. ed.). International Thomson Publishing.

45. Any context-free language is
generated by a context-free
grammar in Chomsky normal
form !!
45
Theorem
Michael Sipser. 1996. Introduction to the Theory of Computation (1st. ed.). International Thomson Publishing.

46. How to convert any
context free grammar to
Chomsky Normal
Form (CNF) ?

47. CFG →CNF
47
Step 1
Eliminate start symbol from the right hand side
If the start symbol is at the RHS of any production in
grammar, create a new start variable and new
production as
Eg, S0
→S
So, S0
becomes the new start variable.

48. CFG →CNF
48
Step 2
Eliminate null, unit and useless productions

49. CFG →CNF
49
Step 3
Eliminate terminals from RHS if they exist with other
terminals or non-terminals
Eg,
X→xY can be decomposed as
X→ZY
Z→x

50. CFG →CNF
50
Step 4
Eliminate RHS with more than two non-terminals
Eg,
X→XZY can be decomposed as
X→PY
P→XZ

51. Examples CFG→CNF

52. CFG →CNF
52
Example 1, Given CFG
eg
S → ASB
A → aAS|a|ε
B → SbS|A|bb

53. CFG →CNF
53
Step 1
eg
As start symbol S appears on the RHS, we will create a new
production rule S0
→ S. Therefore, the grammar will become
S0
→S
S→ASB
A→aAS|a|ε
B→SbS|A|bb

54. CFG →CNF
54
Step 2
eg
As grammar contains null production A→ε and B→ε, its removal
from the grammar yields
S0
→S
S→AS|ASB|SB|S
A→aAS|aS|a
B→SbS|A|bb

55. CFG →CNF
55
Step 2 (continued)
eg
As grammar contains null production B→A and S0
→S, its removal
from the grammar yields
S0
→AS|ASB|SB|S
S→AS|ASB|SB|S
A→aAS|aS|a
B→SbS|aAS|aS|a|bb

56. CFG →CNF
56
Step 3
eg
terminals a and b exist on RHS with non-terminates. Removing
them from RHS
S0
→AS|ASB|SB
S→AS|ASB|SB
A→XAS|XS|a
B→SYS|bb|XAS|XS|a
X→a
Y→b

57. CFG →CNF
57
Step 3
eg
B→bb can’t be part of CNF, removing it from grammar yields
S0
→AS|ASB|SB
S→AS|ASB|SB
A→XAS|XS|a
B→SYS|VV|XAS|XS|a
X→a
Y→b
V→b

58. CFG →CNF
58
Step 4
eg
Eliminating RHS with more than two non-terminals, finally we get

59. CFG →CNF
59
Step 4
eg
S0
→ AS|PB|SB
S → AS|QB|SB
A → RS|XS|a
B → TS|VV|US|XS|a
X → a
Y → b
V → b
P → AS
Q → AS
R → XA
T → SY
U → XA

60. CFG →CNF
60
Example 2, Given CFG
eg
S → ASA | aB
A → B | S
B → b | ε

61. CFG →CNF
61
Example 2, CNF
eg
S0→ AX | YB | a | AS | SA
S→ AX | YB | a | AS | SA
A → b |AX | YB | a | AS | SA
B → b
X → SA
Y → a

62. 62
Thank
You!