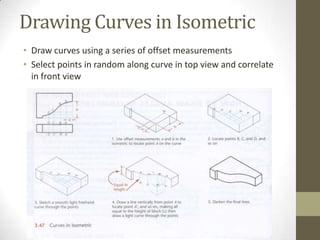
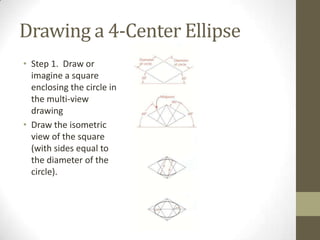
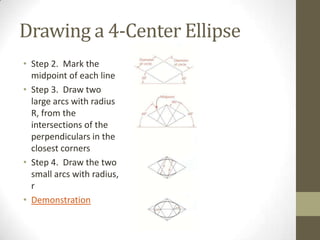
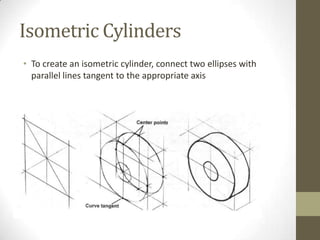
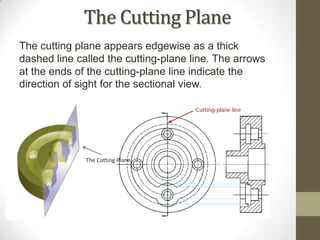
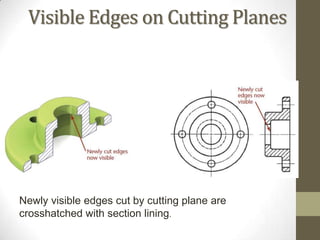
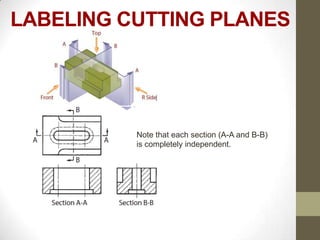
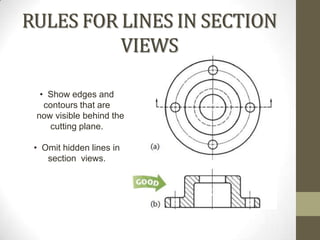
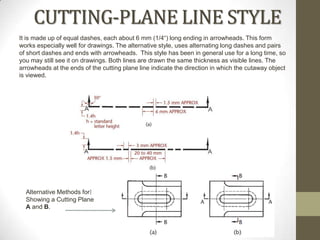
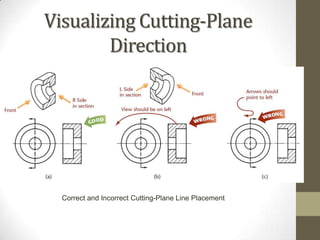
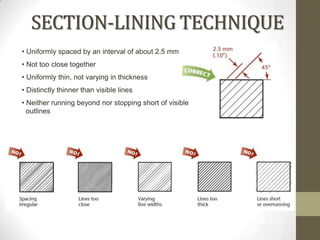
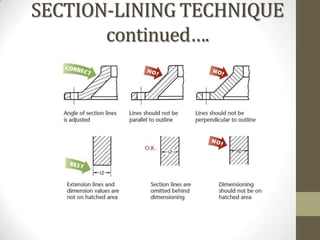
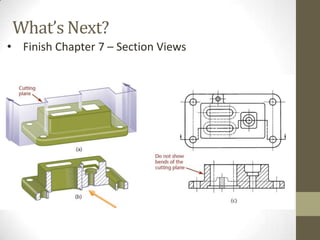
This document provides an overview of a 2D Essentials class being taught from January 18th to May 16th. It covers topics like isometric drawings, axonometric projections, drawing curves and holes in isometric views, and section views. Reminders are provided about upcoming project deadlines. Examples are given for techniques like drawing oblique surfaces, angles, cylinders, and screw threads in isometric. Students will complete group projects applying these techniques and visualizing exercises are linked to reinforce learning. The next class will finish the chapter on section views and address any remaining questions. Homework includes exercises from chapters 3 and 7.

1. 2D Essentials
Instructor: Laura Gerold, PE
Catalog #10614113
Class # 22784, 24113, 24136, & 24138
Class Start: January 18, 2012
Class End: May 16, 2012

2. Reminders
• 50% Project Plans are due next TODAY!
• Final Project is due on May 9th.
• Optional extra credit is due next week on April 11th
• Find other countries where 1st and 3rd angle projections are used
for 5 extra points
• Details are on blackboard in class materials / extra credit folder

3. Chapter 3 – Isometric
Drawing

4. Group Project
• Individually Create an object using your blocks.
• Draw an isometric drawing of your creations.
• Trade your drawing with someone in a different row.
• With a new drawing in hand from someone else, create the
object on the plan using your blocks.
• Questions
• Can you create the object with an isometric drawing only?
• Was it easier or harder than creating an object using the
orthographic plans?
• Which method would you prefer, or would you like both for
creating a part in the “real-world?”

5. Axonometric Drawings
• Axonometric projection is a type of
parallel projection, more specifically a
type of orthographic projection, used to
create a pictorial drawing of an object,
where the object is rotated along one or
more of its axes relative to the plane of
projection.
• Different from orthographic because of
the angle the object is “tipped”
• "Axonometric" means "to measure
along axes". There are three axes.
• There are three main types of
axonometric projection: isometric,
dimetric, and trimetric projection.

6. Axonometric Drawings
• Foreshortening – reducing the length of a line to create an
illusion of an object being in 3D
• Isometric Projection – equal foreshortening along each of the
three axis
• Isometric is the most common form of axonometric projection
used.

7. Axonometric Drawings
• Dimetric Projection – equal foreshortening along two axis, and
a different along the third axis. Not “tipped” evenly on all
planes of projection.
Source: http://draftingmanuals.tpub.com/14276/css/14276_326.htm

8. Axonometric Drawings
• Trimetric projection – different foreshortening along all three
axis directions
Source: http://draftingmanuals.tpub.com/14276/css/14276_327.htm

9. Isometric Lines
• The projections of the edges of a cube make angles of 120
degrees to each other (isometric axes)
• Any line parallel to one of these lines is called an isometric
line
• Isometric Lines are used to draw normal edges

10. Non-Isometric Lines
• Non-Isometric Lines are lines that are not parallel to the
isometric axes
• The lengths of non-isometric lines cannot be measured
directly with a scale
• Non-isometric lines are used to draw inclined & oblique
surfaces

11. Oblique Surfaces in Isometric
• Step 1: Find the intersections of the oblique surfaces with the
isometric planes.
• Note that for this example, the oblique plane contains point A,
B, and C

12. Oblique Surfaces in Isometric
• Step 2: To draw the plane, extend line AB to X and Y, in the
same isometric plane as C
• Use lines XC and YC to locate points E and F

13. Oblique Surfaces in Isometric
• Step 3: Finally draw AD and ED using the rule that parallel
lines appear parallel in every orthographic or isometric view

14. Group Project - Oblique
Surfaces in Isometric
• Create a simple isometric sketch of an oblique surface. Use
items you brought, items in the room, or go on a quick
scavenger hunt around the 2nd floor
• Label the isometric and non-isometric lines
• Shade in the oblique planes
• Present your drawing as a group to the class

15. Hidden Lines and Centerlines
• Hidden lines are omitted from pictorial drawings unless they
are needed to make the drawing clear
• Draw centerlines locating the center of a hole only if they are
needed to indicate symmetry or for dimensioning
• Use centerlines sparingly in isometric drawings - “If in doubt,
leave them out”

16. Angles in Isometric
• Angles project true size only when the plane containing the
angle is parallel to the plane of projection
• An angle may project to appear larger or smaller than the true
angle depending on its position

17. Drawing Angles in Isometric
• The multi-view below shows three 60 degree angles. None of
the three angles will be 60 degrees in the isometric drawing.

18. Drawing Angles in Isometric
• Step 1. Lightly draw an enclosing box
using the given dimensions, except
for dimension X, which is not given.
• Step 2. To find X, draw triangle BDA
from the top view full size as shown.
• Step 3. Transfer dimension X to the
isometric drawing to complete the
enclosing box Find dimension Y by a
similar method and then transfer it to
the isometric.
• Step 4. Use dimension K to locate
point E. A protractor can’t be used to
measure angles in a isometric
drawing . Convert angular
measurements to linear
measurements along isometric axes.

19. Group Project - Angles in
Isometric
• Draw a multi-view (orthographic) sketch of a triangle with
three angles, 30, 60, and 90 on the front view, with a depth
and width of your choice.
• Create an isometric drawing using your orthographic sketch
• Present

20. Drawing Curves in Isometric
• Draw curves using a series of offset measurements
• Select points in random along curve in top view and correlate
in front view

21. Drawing Holes in Isometric
• When a circle lies in a plane that is not parallel to the plane of
projection, the circle projects as an ellipse.
• The ellipse can be constructed using offset measurements.
• There are several different methods that can be used to draw
an isometric ellipse . . . We’ll cover a couple in class.

22. Isometric Ellipse – Random
Line Method
• Step 1: Draw parallel lines
spaced at random across
the circle
• Step 2: Transfer these lines
to the isometric drawing

23. Isometric Ellipse in a non-
isometric plane
• If the curve lies on a non-isometric plane (it is inclined or
oblique), can not directly apply offset measurements
• Step 1. Draw lines in the orthographic view to locate points

24. Isometric Ellipse in a non-
isometric plane
• Step 2 Enclose the cylinder in a construction box and draw
the box in the isometric drawing
• Draw the base using offset measurements
• Construct the inclined ellipse by locating points and drawing
the final curve through them

25. Isometric Ellipse in a non-
isometric plane
• Step 3: Darken the final lines

26. Orienting Ellipses in Isometric
• All diagonals on an isometric cube are horizontal or are at 60
degrees to the horizontal
• Approximate ellipses drawn using the four center method are
accurate enough for most isometric drawings

27. Drawing a 4-Center Ellipse
• Step 1. Draw or
imagine a square
enclosing the circle in
the multi-view
drawing
• Draw the isometric
view of the square
(with sides equal to
the diameter of the
circle).

28. Drawing a 4-Center Ellipse
• Step 2. Mark the
midpoint of each line
• Step 3. Draw two
large arcs with radius
R, from the
intersections of the
perpendiculars in the
closest corners
• Step 4. Draw the two
small arcs with radius,
r
• Demonstration

29. Group Project - Isometric
Ellipses
• Use your blocks to build a simple object
• Draw the object in isometric complete with holes show as
isometric ellipse
• If you brought an item with holes , you can draw that item
instead
• Present drawings

30. Isometric Cylinders
• To create an isometric cylinder, connect two ellipses with
parallel lines tangent to the appropriate axis

31. Group Project – Isometric
Cylinders
• Use an object you brought, that I have, or that you find in a
room and draw an isometric cylinder
• Present results

32. Screw Threads in Isometric
• Use parallel partial ellipses equally spaced at the symbolic
thread pitch to represent the crests of a screw thread in
isometric

33. Visualization Exercise
• http://www.wisc-
online.com/objects/ViewObject.aspx?ID=ENG20004

34. Chapter 7 – Section
Views

35. Why do we need Section
Views?
• To see what is “hidden” within a item to be able to build it
• To show the material that the item is built out of
• How-To Architect

36. UNDERSTANDING SECTIONS
Section views are used for three main purposes:
• To document the design and manufacture of single parts that are manufactured as one
piece.
• To document how multiple parts are to be assembled or built.
• To aid in visualizing the internal workings of a design.
When the part is cut fully
in half, the resulting view
is called a full section.

37. The Cutting Plane
The cutting plane appears edgewise as a thick
dashed line called the cutting-plane line. The arrows
at the ends of the cutting-plane line indicate the
direction of sight for the sectional view.
The Cutting Plane

38. Visible Edges on Cutting Planes
Newly visible edges cut by cutting plane are
crosshatched with section lining.

39. LABELING CUTTING PLANES
Note that each section (A-A and B-B)
is completely independent.

40. RULES FOR LINES IN SECTION
VIEWS
• Show edges and
contours that are
now visible behind the
cutting plane.
• Omit hidden lines in
section views.

41. RULES FOR LINES IN SECTION
VIEWS
• Show edges and contours
that are now visible behind the
cutting plane.
• Omit hidden lines in section
views.
• A sectioned area is always
completely bounded by a
visible outline—never by a
hidden line.
• A visible line can never
cross a sectioned area in a
view of a single part.

42. CUTTING-PLANE LINE STYLE
It is made up of equal dashes, each about 6 mm (1/4“) long ending in arrowheads. This form
works especially well for drawings. The alternative style, uses alternating long dashes and pairs
of short dashes and ends with arrowheads. This style has been in general use for a long time, so
you may still see it on drawings. Both lines are drawn the same thickness as visible lines. The
arrowheads at the ends of the cutting plane line indicate the direction in which the cutaway object
is viewed.
Alternative Methods for
Showing a Cutting Plane
A and B.

43. Visualizing Cutting-Plane
Direction
Correct and Incorrect Cutting-Plane Line Placement

44. SECTION-LINING TECHNIQUE
• Uniformly spaced by an interval of about 2.5 mm
• Not too close together
• Uniformly thin, not varying in thickness
• Distinctly thinner than visible lines
• Neither running beyond nor stopping short of visible
outlines

45. SECTION-LINING TECHNIQUE
continued….

46. Group Project - Section Views
• Draw a section view of a simple object (blocks?) in the room

47. Section Views Visualization
Exercise
• http://www.wisc-
online.com/objects/ViewObject.aspx?ID=ENG19804

48. What’s Next?
• Finish Chapter 7 – Section Views

49. Questions?
• On one of your sketches, answer the following two questions:
• What was the most useful thing that you learned today?
• What do you still have questions about?

50. Homework
Chapter 3 Exercises: 3.1 (h, i – isometric sketch only)
Chapter 7 Review Questions: 1