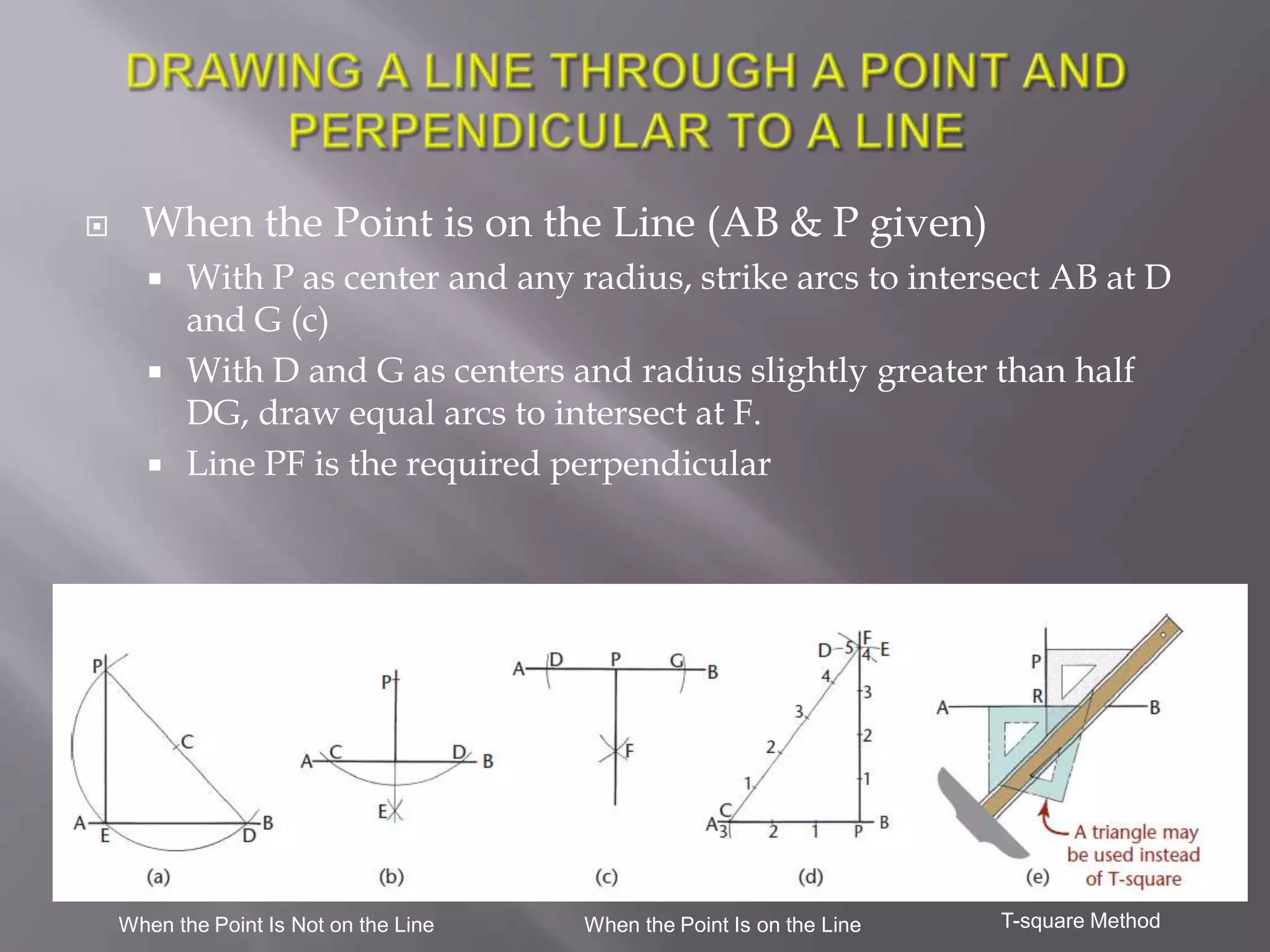
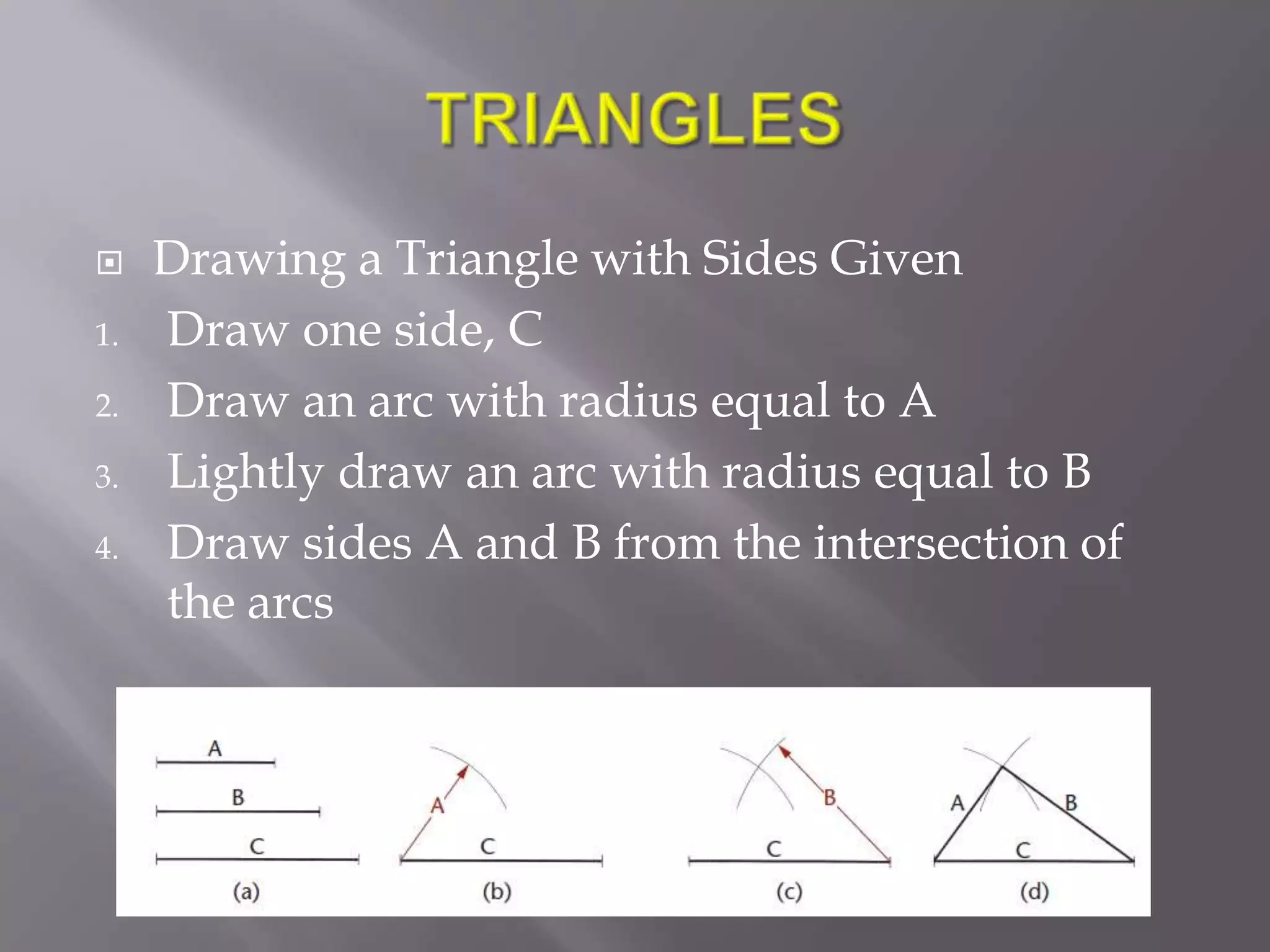
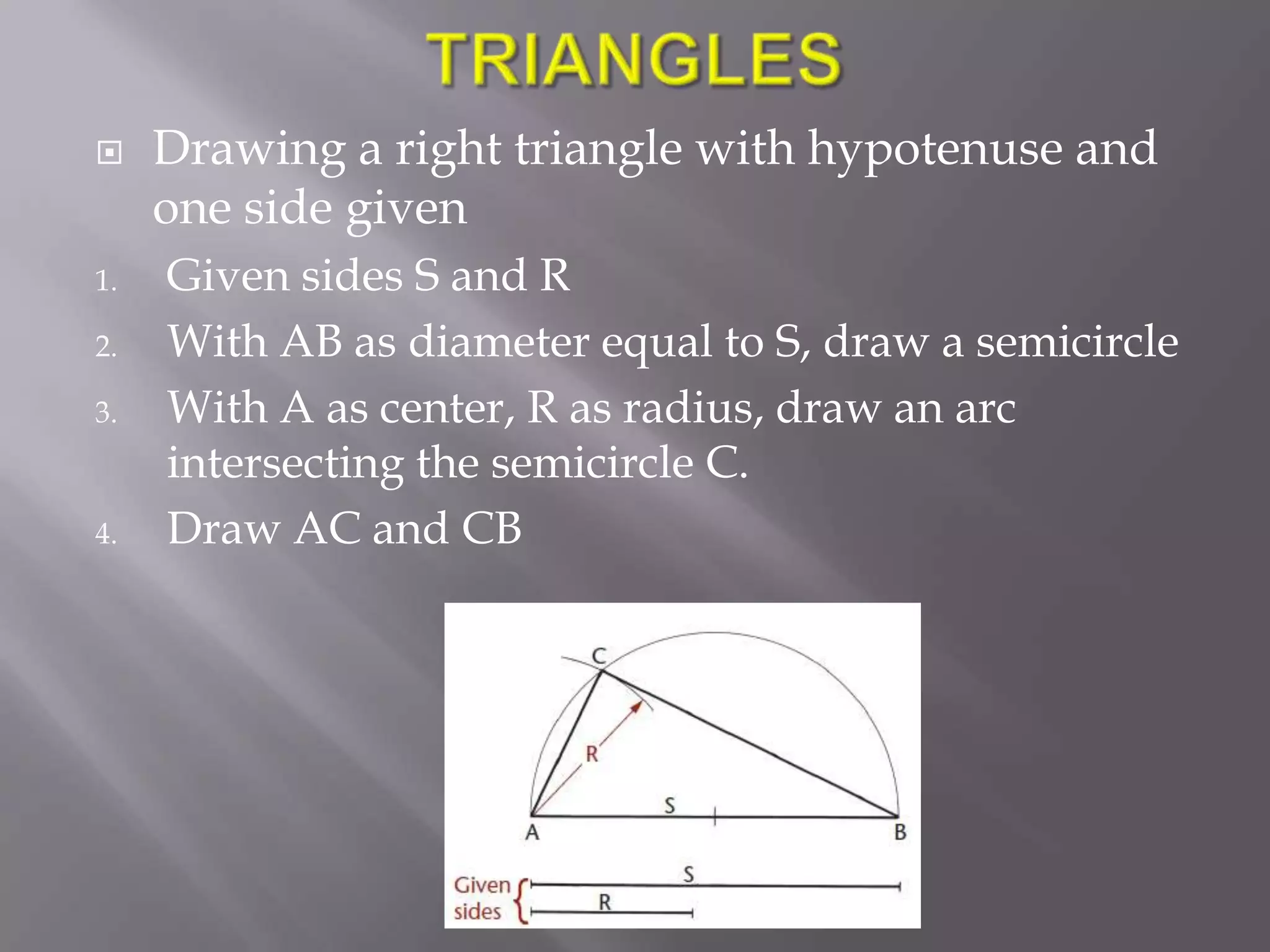
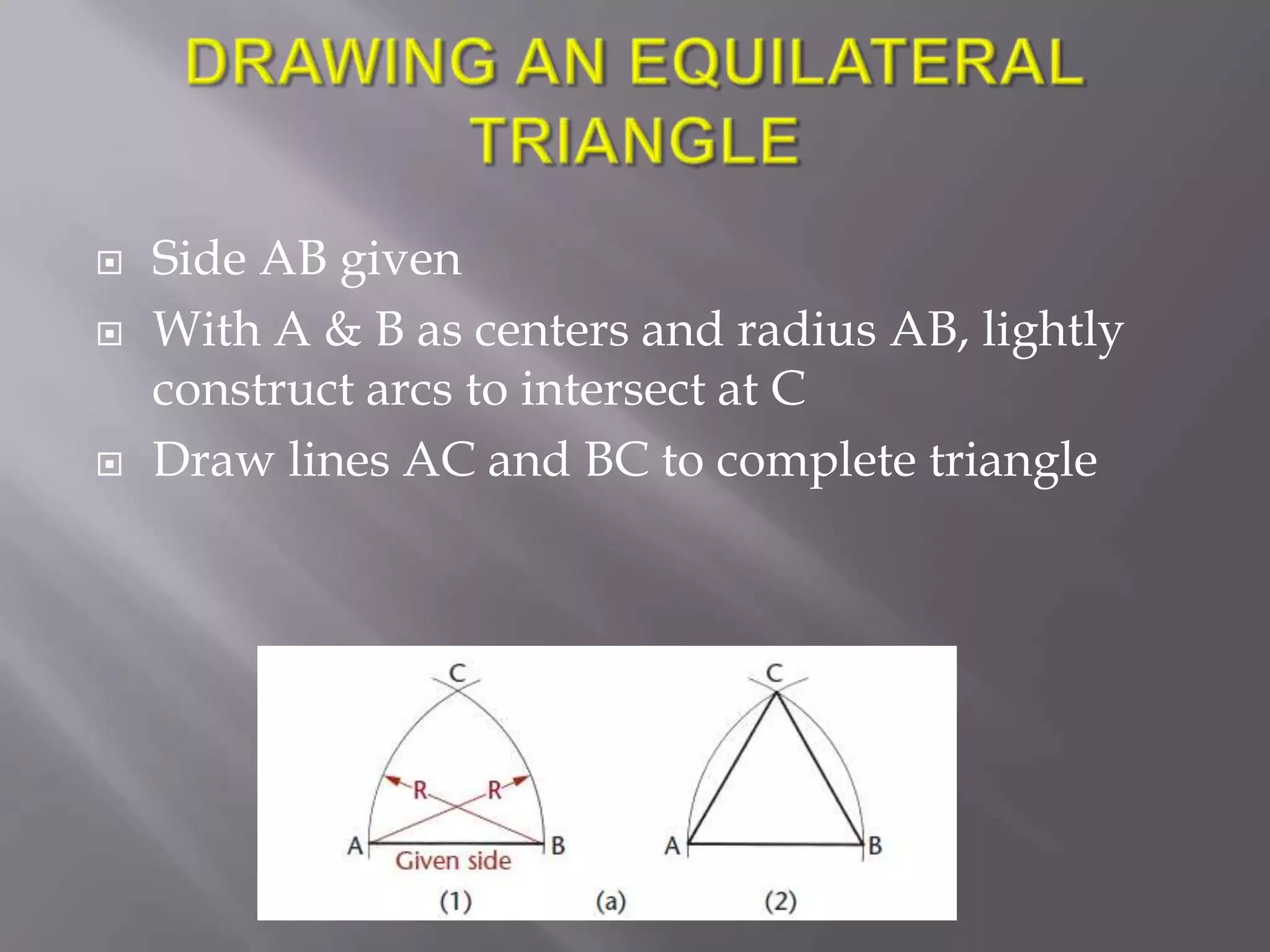
Here are the steps to draw an equilateral triangle using the diameters method:
1. Draw a circle of any convenient size.
2. Draw two diameters of the circle that intersect at right angles. These will form the bases of the triangle.
3. With the points where the diameters intersect the circle as centers, and using the radius of the circle as the radius, draw arcs above the diameters.
4. The point where the arcs intersect will be the third vertex of the equilateral triangle.
5. Connect this point to the two base points to complete the equilateral triangle.
The key steps are using the diameters of the circle as the bases, and the fact that arcs drawn with the same