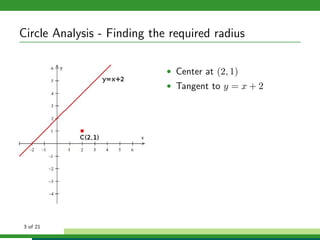
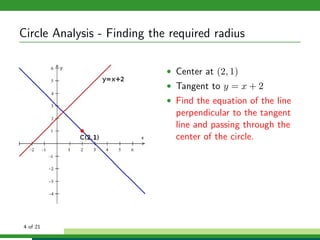
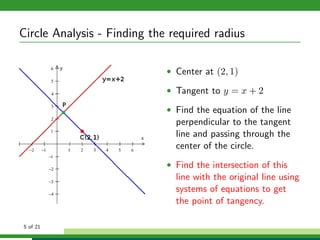
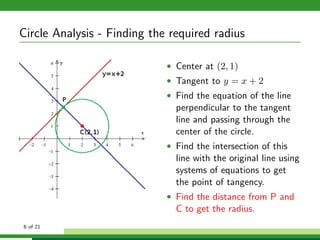
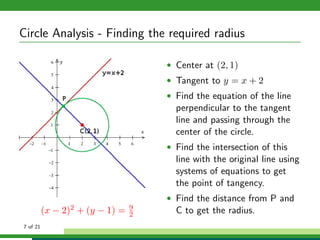
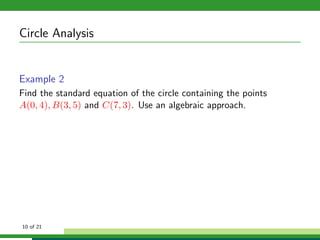
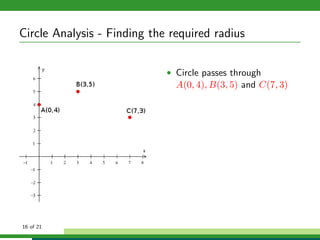
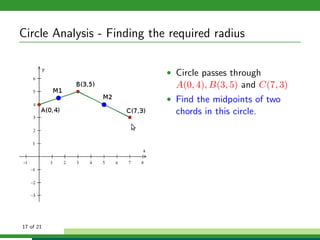
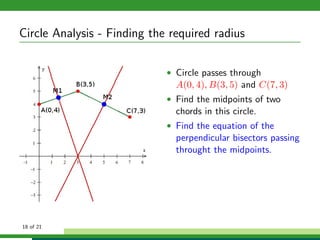
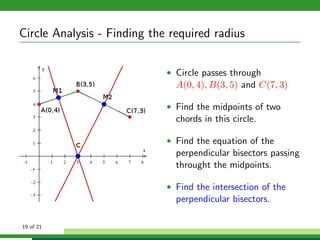
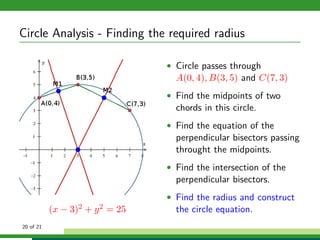
This document provides examples and explanations for analyzing problems involving circles. It begins by working through an example of finding the equation of a circle tangent to a given line with a specified center. It then discusses using an algebraic approach to find the standard equation of a circle passing through three given points by setting up three equations and solving simultaneously for the center and radius. Finally, it covers using a geometric approach involving finding the perpendicular bisectors of chord midpoints and their intersection to determine the circle's center. The document aims to demonstrate different methods for solving circle geometry problems.

1. Circles - Analysis Problems
Mathematics 4
August 15, 2011
1 of 21

2. Circle Analysis
Example 1
A circle with center (2, 1) is tangent to the line y = x + 2. Find the
equation of this circle.
2 of 21

3. Circle Analysis
Example 1
A circle with center (2, 1) is tangent to the line y = x + 2. Find the
equation of this circle.
What do we need to solve for?
2 of 21

4. Circle Analysis
Example 1
A circle with center (2, 1) is tangent to the line y = x + 2. Find the
equation of this circle.
What do we need to solve for? → the radius of the circle.
2 of 21

5. Circle Analysis
Example 1
A circle with center (2, 1) is tangent to the line y = x + 2. Find the
equation of this circle.
What do we need to solve for? → the radius of the circle.
What do we know?
2 of 21

6. Circle Analysis
Example 1
A circle with center (2, 1) is tangent to the line y = x + 2. Find the
equation of this circle.
What do we need to solve for? → the radius of the circle.
What do we know?
1. The tangent line is perpendicular to the line passing through the
radius and point of tangency.
2. To get the value of the radius, we need to find the coordinates of
the point of tangency.
2 of 21

7. Circle Analysis - Finding the required radius
• Center at (2, 1)
• Tangent to y = x + 2
3 of 21

8. Circle Analysis - Finding the required radius
• Center at (2, 1)
• Tangent to y = x + 2
• Find the equation of the line
perpendicular to the tangent
line and passing through the
center of the circle.
4 of 21

9. Circle Analysis - Finding the required radius
• Center at (2, 1)
• Tangent to y = x + 2
• Find the equation of the line
perpendicular to the tangent
line and passing through the
center of the circle.
• Find the intersection of this
line with the original line using
systems of equations to get
the point of tangency.
5 of 21

10. Circle Analysis - Finding the required radius
• Center at (2, 1)
• Tangent to y = x + 2
• Find the equation of the line
perpendicular to the tangent
line and passing through the
center of the circle.
• Find the intersection of this
line with the original line using
systems of equations to get
the point of tangency.
• Find the distance from P and
C to get the radius.
6 of 21

11. Circle Analysis - Finding the required radius
• Center at (2, 1)
• Tangent to y = x + 2
• Find the equation of the line
perpendicular to the tangent
line and passing through the
center of the circle.
• Find the intersection of this
line with the original line using
systems of equations to get
the point of tangency.
• Find the distance from P and
9
(x − 2)2 + (y − 1) = 2 C to get the radius.
7 of 21

12. Recitation Problem
For 2 reci points
Find the standard equation of a circle tangent to y = 2x + 11 and
whose center is at C(1, 3).
• 1 reci point for the point of tangency
• 1 reci point for the standard equation
8 of 21

13. Recitation Problem
For 2 reci points
Find the standard equation of a circle tangent to y = 2x + 11 and
whose center is at C(1, 3).
• 1 reci point for the point of tangency → P (−3, 5)
• 1 reci point for the standard equation → (x − 1)2 + (y − 3)2 = 20.
9 of 21

14. Circle Analysis
Example 2
Find the standard equation of the circle containing the points
A(0, 4), B(3, 5) and C(7, 3). Use an algebraic approach.
10 of 21

15. Circle Analysis
Example 2
Find the standard equation of the circle containing the points
A(0, 4), B(3, 5) and C(7, 3). Use an algebraic approach.
What do we need to solve for?
10 of 21

16. Circle Analysis
Example 2
Find the standard equation of the circle containing the points
A(0, 4), B(3, 5) and C(7, 3). Use an algebraic approach.
What do we need to solve for? → the radius and center of the circle.
10 of 21

17. Circle Analysis
Example 2
Find the standard equation of the circle containing the points
A(0, 4), B(3, 5) and C(7, 3). Use an algebraic approach.
What do we need to solve for? → the radius and center of the circle.
What do we know?
10 of 21

18. Circle Analysis
Example 2
Find the standard equation of the circle containing the points
A(0, 4), B(3, 5) and C(7, 3). Use an algebraic approach.
What do we need to solve for? → the radius and center of the circle.
What do we know?
1. The standard equation of the circle is (x − h)2 + (y − k)2 = r2
2. Three different points satisfying this equation.
10 of 21

19. Circle Analysis
Example 2
Find the standard equation of the circle containing the points
A(0, 4), B(3, 5) and C(7, 3). Use an algebraic approach.
What do we need to solve for? → the radius and center of the circle.
What do we know?
1. The standard equation of the circle is (x − h)2 + (y − k)2 = r2
2. Three different points satisfying this equation.
What do we need to do?
10 of 21

20. Circle Analysis
Example 2
Find the standard equation of the circle containing the points
A(0, 4), B(3, 5) and C(7, 3). Use an algebraic approach.
What do we need to solve for? → the radius and center of the circle.
What do we know?
1. The standard equation of the circle is (x − h)2 + (y − k)2 = r2
2. Three different points satisfying this equation.
What do we need to do? → Find the values for h, k and r2 .
10 of 21

21. Circle Analysis - A(0, 4), B(3, 5) and C(7, 3).
Construct 3 equations using the standard equation and each of the
three points.
11 of 21

22. Circle Analysis - A(0, 4), B(3, 5) and C(7, 3).
Construct 3 equations using the standard equation and each of the
three points.
1. (0 − h)2 + (4 − k)2 = r2
2. (3 − h)2 + (5 − k)2 = r2
3. (7 − h)2 + (3 − k)2 = r2
11 of 21

23. Circle Analysis - A(0, 4), B(3, 5) and C(7, 3).
Construct 3 equations using the standard equation and each of the
three points.
1. (0 − h)2 + (4 − k)2 = r2
2. (3 − h)2 + (5 − k)2 = r2
3. (7 − h)2 + (3 − k)2 = r2
Equate the equations since they are all equal to r2 .
1 = 2 (0 − h)2 + (4 − k)2 = (3 − h)2 + (5 − k)2
2 = 3 (3 − h)2 + (5 − k)2 = (7 − h)2 + (3 − k)2
11 of 21

24. Circle Analysis - A(0, 4), B(3, 5) and C(7, 3).
Construct 3 equations using the standard equation and each of the
three points.
1. (0 − h)2 + (4 − k)2 = r2
2. (3 − h)2 + (5 − k)2 = r2
3. (7 − h)2 + (3 − k)2 = r2
Equate the equations since they are all equal to r2 .
1 = 2 (0 − h)2 + (4 − k)2 = (3 − h)2 + (5 − k)2 → 3h + k = 9 (A)
2 = 3 (3 − h)2 + (5 − k)2 = (7 − h)2 + (3 − k)2 → 2h − k = 6 (B)
12 of 21

25. Circle Analysis - A(0, 4), B(3, 5) and C(7, 3).
Solving Equations A and B simultaneously:
13 of 21

26. Circle Analysis - A(0, 4), B(3, 5) and C(7, 3).
Solving Equations A and B simultaneously:
3h + k = 9
2h − k = 6
13 of 21

27. Circle Analysis - A(0, 4), B(3, 5) and C(7, 3).
Solving Equations A and B simultaneously:
3h + k = 9
2h − k = 6
We get the center to be (3, 0).
13 of 21

28. Circle Analysis - A(0, 4), B(3, 5) and C(7, 3).
Solving Equations A and B simultaneously:
3h + k = 9
2h − k = 6
We get the center to be (3, 0).
Find the radius by substituting (3, 0) to any of the first three
equations we generated.
13 of 21

29. Circle Analysis - A(0, 4), B(3, 5) and C(7, 3).
Solving Equations A and B simultaneously:
3h + k = 9
2h − k = 6
We get the center to be (3, 0).
Find the radius by substituting (3, 0) to any of the first three
equations we generated.
(0 − 3)2 + (4 − 0)2 = r2
9 + 16 = r2
13 of 21

30. Circle Analysis - A(0, 4), B(3, 5) and C(7, 3).
Solving Equations A and B simultaneously:
3h + k = 9
2h − k = 6
We get the center to be (3, 0).
Find the radius by substituting (3, 0) to any of the first three
equations we generated.
(0 − 3)2 + (4 − 0)2 = r2
9 + 16 = r2
Final standard equation: (x − 3)2 + y 2 = 25
13 of 21

31. Recitation Problem
Reci Problem 2
Find the general equation of the circle containing the points
A(−5, 0), B(1, 0), and C(−2, −3).
14 of 21

32. Recitation Problem
Reci Problem 2
Find the general equation of the circle containing the points
A(−5, 0), B(1, 0), and C(−2, −3).
x2 + y 2 + 4x − 5 = 0
14 of 21

33. Circle Analysis
Example 3
Find the standard equation of the circle containing the points
A(0, 4), B(3, 5) and C(7, 3). Use a geometric approach.
15 of 21

34. Circle Analysis
Example 3
Find the standard equation of the circle containing the points
A(0, 4), B(3, 5) and C(7, 3). Use a geometric approach.
What do we need to solve for?
15 of 21

35. Circle Analysis
Example 3
Find the standard equation of the circle containing the points
A(0, 4), B(3, 5) and C(7, 3). Use a geometric approach.
What do we need to solve for? → the radius and center of the circle.
15 of 21

36. Circle Analysis
Example 3
Find the standard equation of the circle containing the points
A(0, 4), B(3, 5) and C(7, 3). Use a geometric approach.
What do we need to solve for? → the radius and center of the circle.
What do we know?
15 of 21

37. Circle Analysis
Example 3
Find the standard equation of the circle containing the points
A(0, 4), B(3, 5) and C(7, 3). Use a geometric approach.
What do we need to solve for? → the radius and center of the circle.
What do we know? → The perpendicular bisectors of chords intersect
at the center.
15 of 21

38. Circle Analysis
Example 3
Find the standard equation of the circle containing the points
A(0, 4), B(3, 5) and C(7, 3). Use a geometric approach.
What do we need to solve for? → the radius and center of the circle.
What do we know? → The perpendicular bisectors of chords intersect
at the center.
What do we need to do?
15 of 21

39. Circle Analysis
Example 3
Find the standard equation of the circle containing the points
A(0, 4), B(3, 5) and C(7, 3). Use a geometric approach.
What do we need to solve for? → the radius and center of the circle.
What do we know? → The perpendicular bisectors of chords intersect
at the center.
What do we need to do?
• Find the equation of the perpendicular bisectors of the midpoints.
15 of 21

40. Circle Analysis
Example 3
Find the standard equation of the circle containing the points
A(0, 4), B(3, 5) and C(7, 3). Use a geometric approach.
What do we need to solve for? → the radius and center of the circle.
What do we know? → The perpendicular bisectors of chords intersect
at the center.
What do we need to do?
• Find the equation of the perpendicular bisectors of the midpoints.
• Find the intersection of the perpendicular bisectors of the
midpoints, which is the center.
15 of 21

41. Circle Analysis
Example 3
Find the standard equation of the circle containing the points
A(0, 4), B(3, 5) and C(7, 3). Use a geometric approach.
What do we need to solve for? → the radius and center of the circle.
What do we know? → The perpendicular bisectors of chords intersect
at the center.
What do we need to do?
• Find the equation of the perpendicular bisectors of the midpoints.
• Find the intersection of the perpendicular bisectors of the
midpoints, which is the center.
• Find the radius by getting the distance from the center to one of
the points in the circle.
15 of 21

42. Circle Analysis - Finding the required radius
• Circle passes through
A(0, 4), B(3, 5) and C(7, 3)
16 of 21

43. Circle Analysis - Finding the required radius
• Circle passes through
A(0, 4), B(3, 5) and C(7, 3)
• Find the midpoints of two
chords in this circle.
17 of 21

44. Circle Analysis - Finding the required radius
• Circle passes through
A(0, 4), B(3, 5) and C(7, 3)
• Find the midpoints of two
chords in this circle.
• Find the equation of the
perpendicular bisectors passing
throught the midpoints.
18 of 21

45. Circle Analysis - Finding the required radius
• Circle passes through
A(0, 4), B(3, 5) and C(7, 3)
• Find the midpoints of two
chords in this circle.
• Find the equation of the
perpendicular bisectors passing
throught the midpoints.
• Find the intersection of the
perpendicular bisectors.
19 of 21

46. Circle Analysis - Finding the required radius
• Circle passes through
A(0, 4), B(3, 5) and C(7, 3)
• Find the midpoints of two
chords in this circle.
• Find the equation of the
perpendicular bisectors passing
throught the midpoints.
• Find the intersection of the
perpendicular bisectors.
• Find the radius and construct
(x − 3)2 + y2 = 25 the circle equation.
20 of 21

47. Recitation Problem
Reci Problem 3
Find the standard equation of the circle containing the points
A(2, 8), B(6, 4) and C(2, 0). Use an geometric approach.
21 of 21

48. Recitation Problem
Reci Problem 3
Find the standard equation of the circle containing the points
A(2, 8), B(6, 4) and C(2, 0). Use an geometric approach.
(x − 2)2 + (y − 4)2 = 16
21 of 21