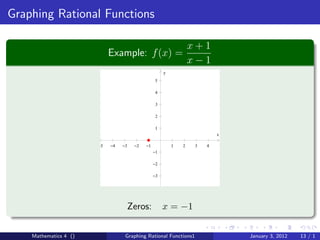
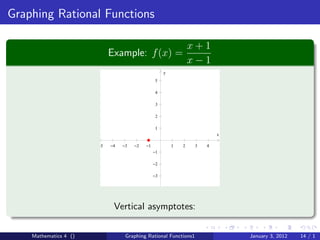
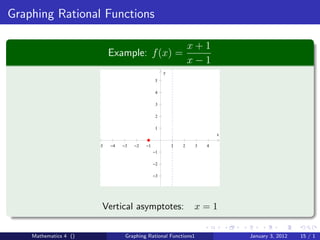
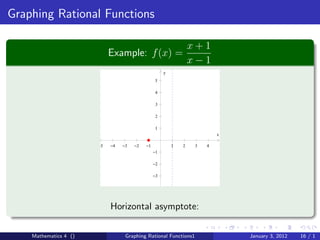
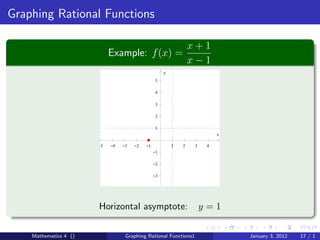
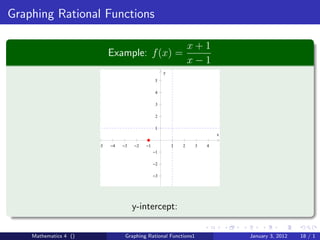
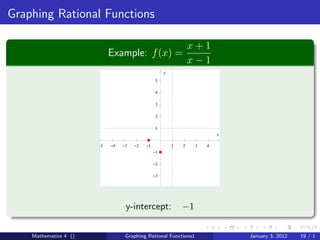
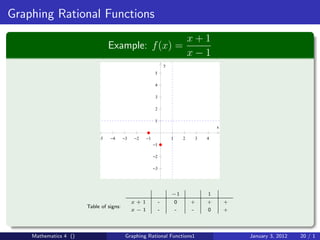
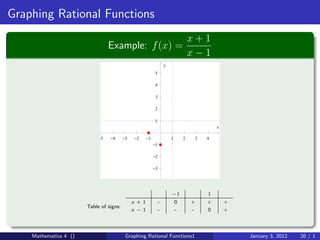
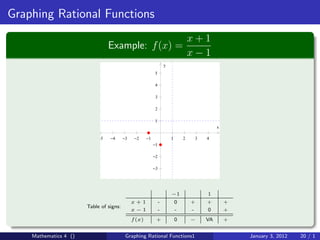
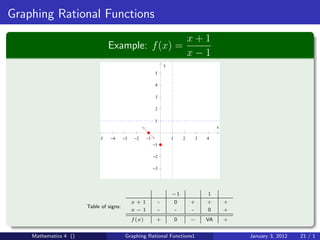
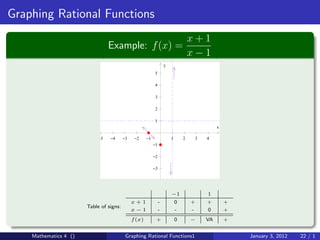
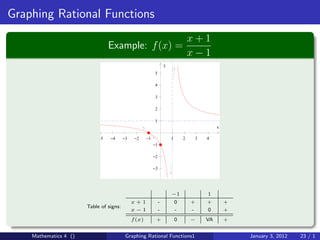
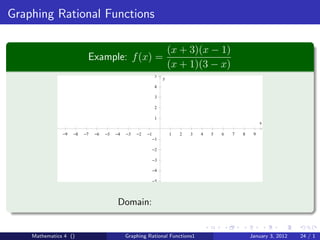
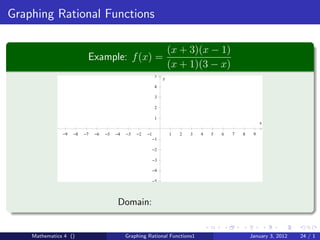
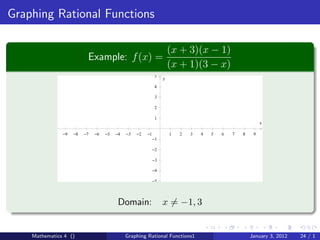
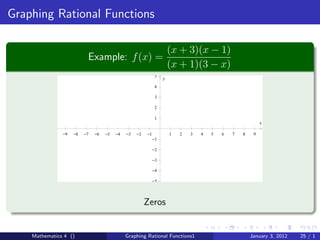
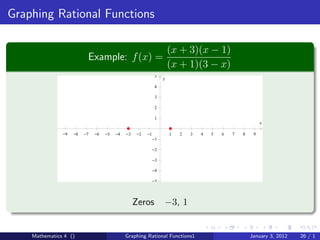
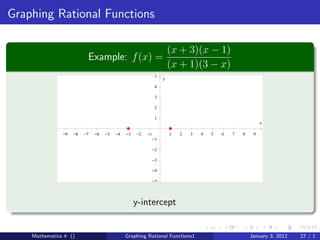
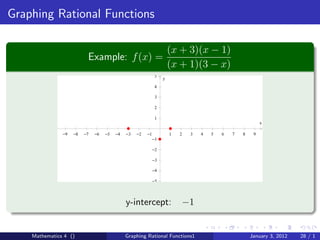
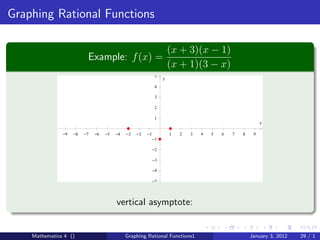
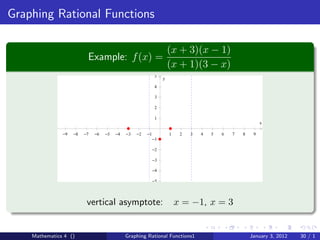
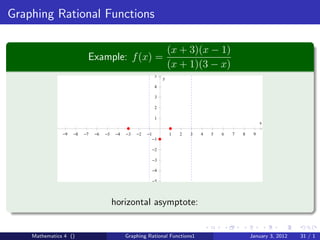
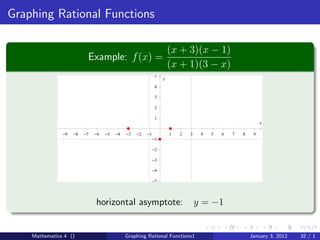
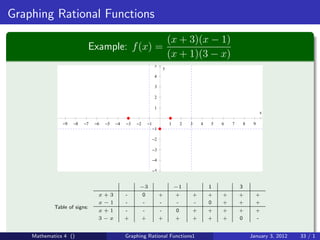
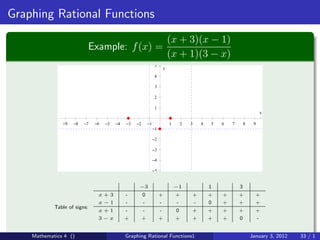
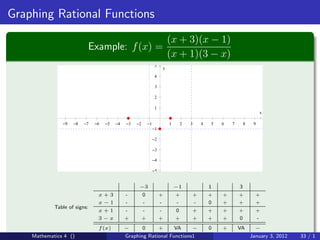
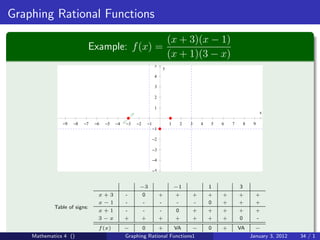
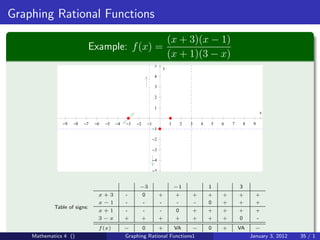
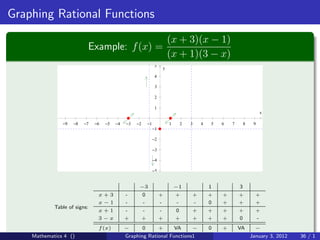
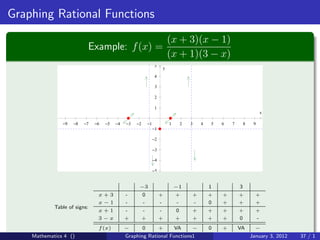
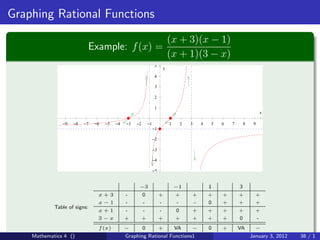
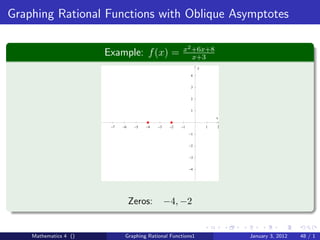
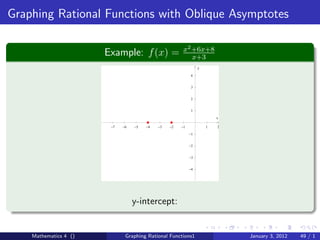
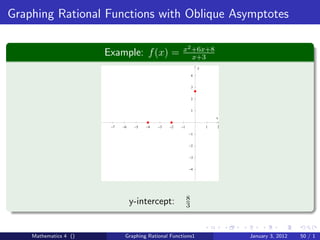
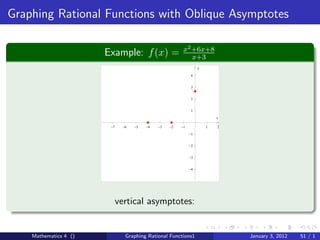
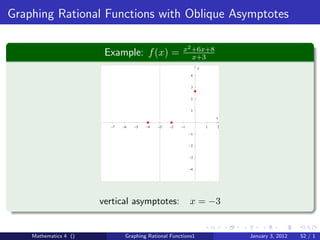
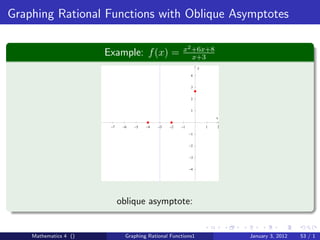
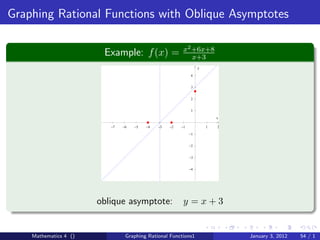
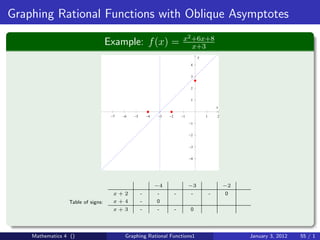
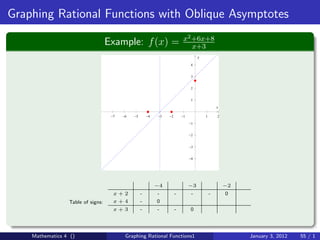
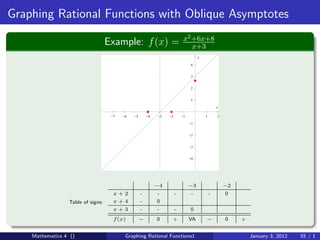
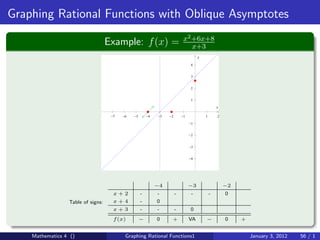
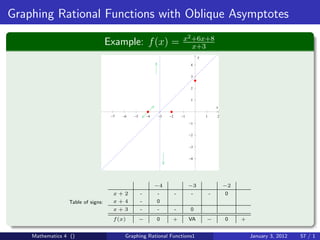
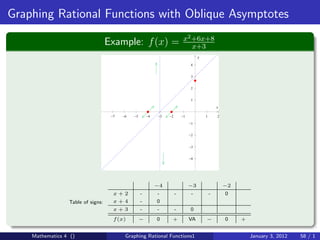
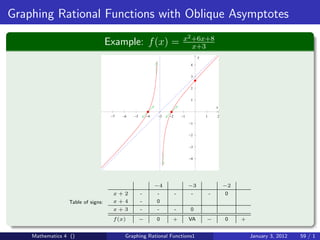
The document discusses rational functions and their key properties for graphing. It defines a rational function as a quotient of two polynomial functions, with the domain being all real numbers except where the denominator is zero. The zeros of the numerator are the zeros of the rational function, and the zeros of the denominator determine the vertical asymptotes. The horizontal asymptote is the line a rational function approaches as x approaches positive and negative infinity. An example demonstrates how to find the horizontal asymptote of a rational function by evaluating it at large positive and negative values of x.