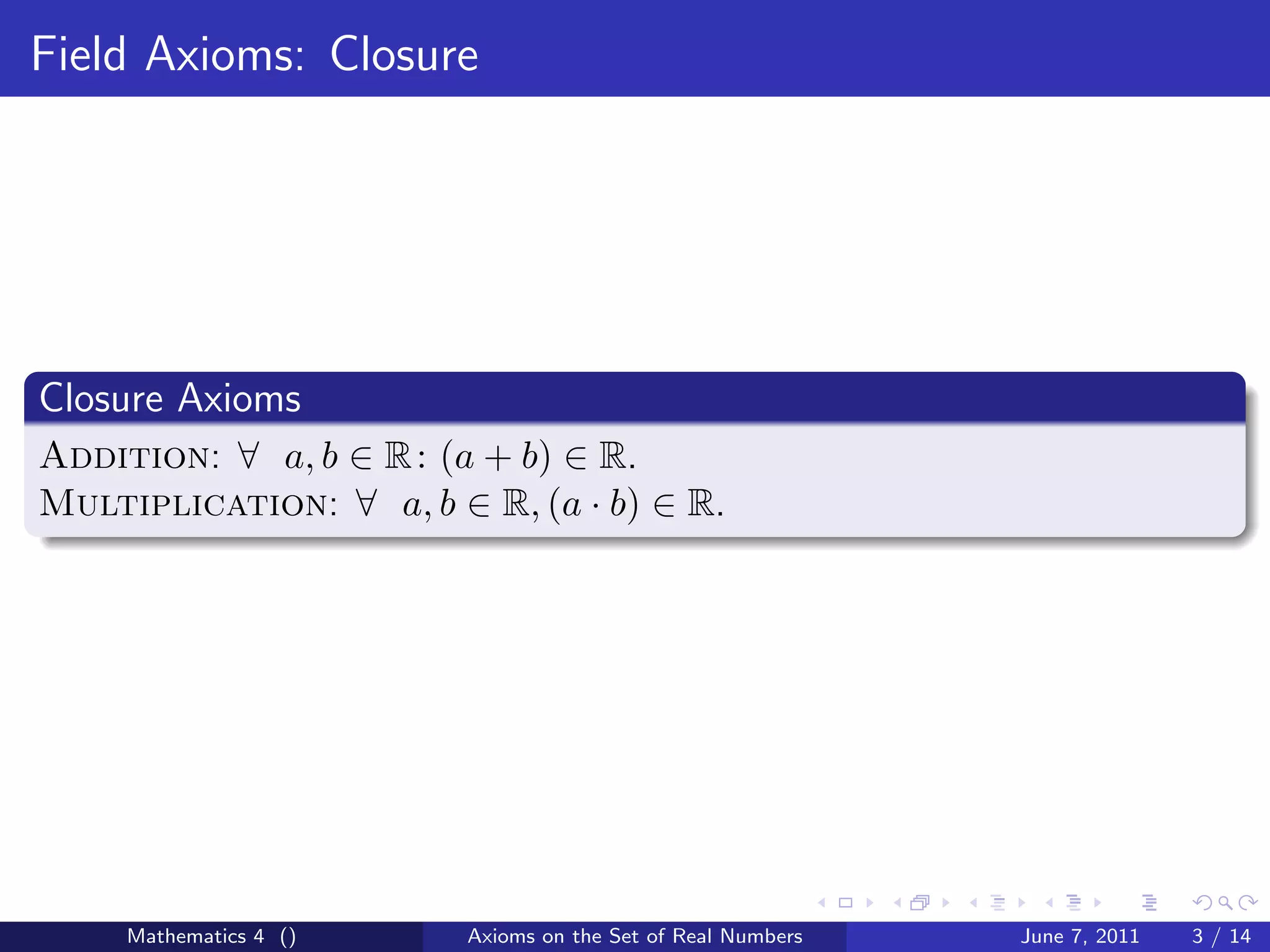
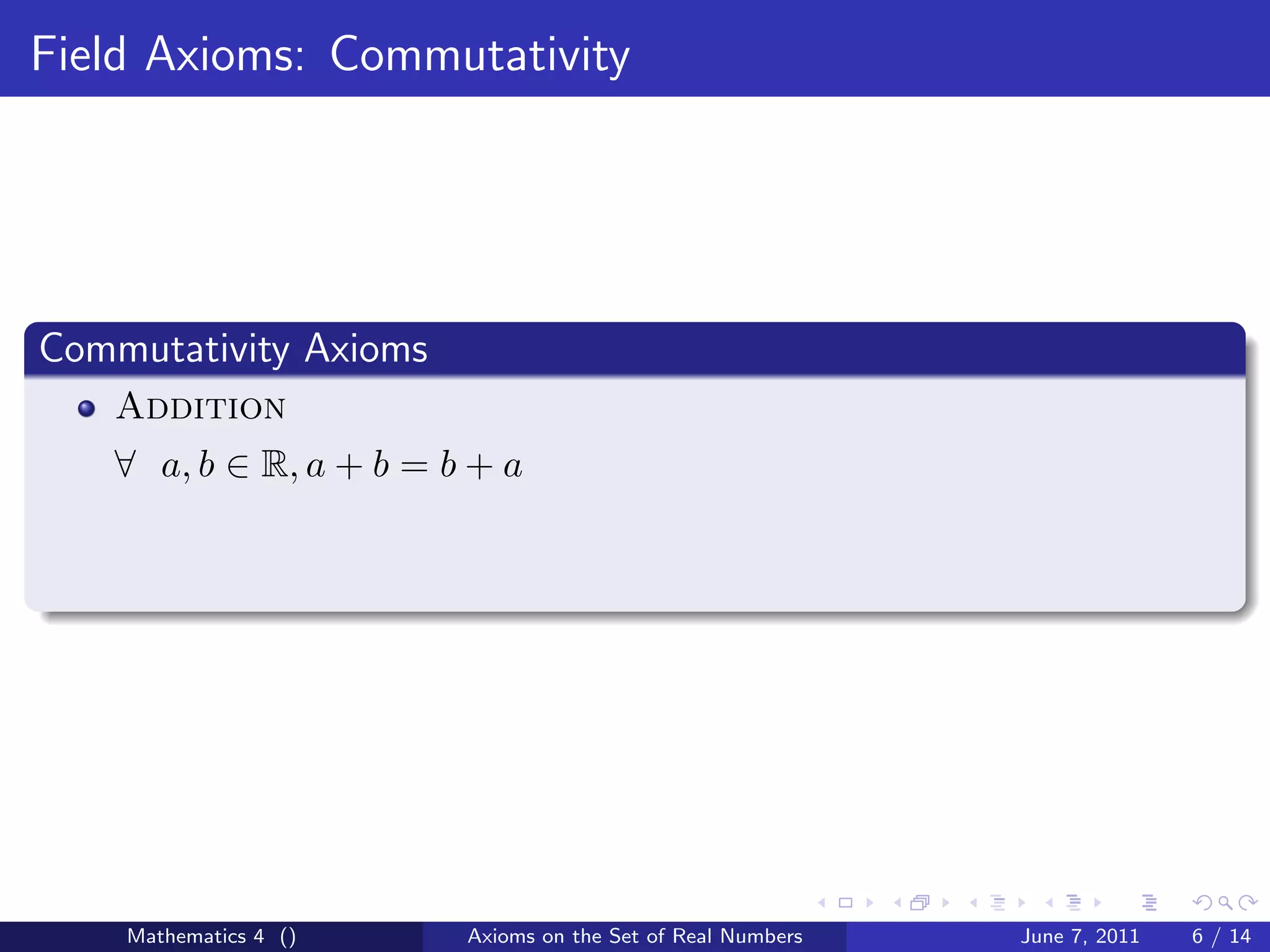
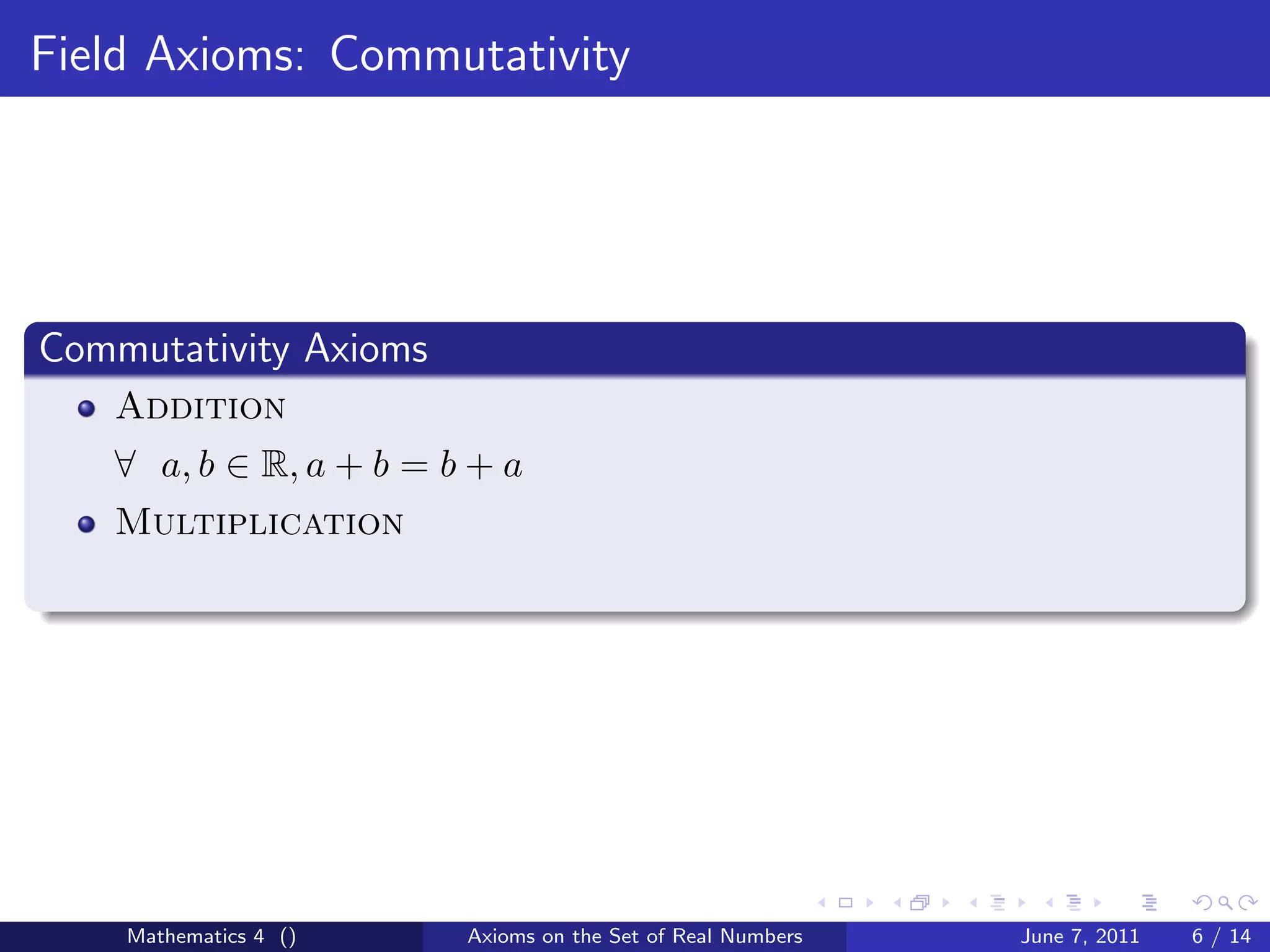
This document discusses the axioms that define a field and the set of real numbers. It outlines the closure, associativity, commutativity, distributive property, identity element, and inverse element axioms for fields. It also covers the equality axioms of reflexivity, symmetry, transitivity, and property extensions for addition and multiplication. The goal is to define the necessary axioms for the set of real numbers to form a field.

1. Axioms on the Set of Real Numbers
Mathematics 4
June 7, 2011
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 1 / 14

2. Field Axioms
Fields
A field is a set where the following axioms hold:
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 2 / 14

3. Field Axioms
Fields
A field is a set where the following axioms hold:
Closure Axioms
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 2 / 14

4. Field Axioms
Fields
A field is a set where the following axioms hold:
Closure Axioms
Associativity Axioms
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 2 / 14

5. Field Axioms
Fields
A field is a set where the following axioms hold:
Closure Axioms
Associativity Axioms
Commutativity Axioms
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 2 / 14

6. Field Axioms
Fields
A field is a set where the following axioms hold:
Closure Axioms
Associativity Axioms
Commutativity Axioms
Distributive Property of Multiplication over Addition
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 2 / 14

7. Field Axioms
Fields
A field is a set where the following axioms hold:
Closure Axioms
Associativity Axioms
Commutativity Axioms
Distributive Property of Multiplication over Addition
Existence of an Identity Element
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 2 / 14

8. Field Axioms
Fields
A field is a set where the following axioms hold:
Closure Axioms
Associativity Axioms
Commutativity Axioms
Distributive Property of Multiplication over Addition
Existence of an Identity Element
Existence of an Inverse Element
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 2 / 14

9. Field Axioms: Closure
Closure Axioms
Addition: ∀ a, b ∈ R : (a + b) ∈ R.
Multiplication: ∀ a, b ∈ R, (a · b) ∈ R.
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 3 / 14

10. Field Axioms: Closure
Identify if the following sets are closed under addition and
multiplication:
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 4 / 14

11. Field Axioms: Closure
Identify if the following sets are closed under addition and
multiplication:
1 Z+
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 4 / 14

12. Field Axioms: Closure
Identify if the following sets are closed under addition and
multiplication:
1 Z+
2 Z−
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 4 / 14

13. Field Axioms: Closure
Identify if the following sets are closed under addition and
multiplication:
1 Z+
2 Z−
3 {−1, 0, 1}
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 4 / 14

14. Field Axioms: Closure
Identify if the following sets are closed under addition and
multiplication:
1 Z+
2 Z−
3 {−1, 0, 1}
4 {2, 4, 6, 8, 10, ...}
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 4 / 14

15. Field Axioms: Closure
Identify if the following sets are closed under addition and
multiplication:
1 Z+
2 Z−
3 {−1, 0, 1}
4 {2, 4, 6, 8, 10, ...}
5 {−2, −1, 0, 1, 2, 3, ...}
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 4 / 14

16. Field Axioms: Closure
Identify if the following sets are closed under addition and
multiplication:
1 Z+
2 Z−
3 {−1, 0, 1}
4 {2, 4, 6, 8, 10, ...}
5 {−2, −1, 0, 1, 2, 3, ...}
6 Q
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 4 / 14

17. Field Axioms: Closure
Identify if the following sets are closed under addition and
multiplication:
1 Z+
2 Z−
3 {−1, 0, 1}
4 {2, 4, 6, 8, 10, ...}
5 {−2, −1, 0, 1, 2, 3, ...}
6 Q
7 Q
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 4 / 14

18. Field Axioms: Associativity
Associativity Axioms
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 5 / 14

19. Field Axioms: Associativity
Associativity Axioms
Addition
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 5 / 14

20. Field Axioms: Associativity
Associativity Axioms
Addition
∀ a, b, c ∈ R, (a + b) + c = a + (b + c)
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 5 / 14

21. Field Axioms: Associativity
Associativity Axioms
Addition
∀ a, b, c ∈ R, (a + b) + c = a + (b + c)
Multiplication
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 5 / 14

22. Field Axioms: Associativity
Associativity Axioms
Addition
∀ a, b, c ∈ R, (a + b) + c = a + (b + c)
Multiplication
∀ a, b, c ∈ R, (a · b) · c = a · (b · c)
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 5 / 14

23. Field Axioms: Commutativity
Commutativity Axioms
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 6 / 14

24. Field Axioms: Commutativity
Commutativity Axioms
Addition
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 6 / 14

25. Field Axioms: Commutativity
Commutativity Axioms
Addition
∀ a, b ∈ R, a + b = b + a
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 6 / 14

26. Field Axioms: Commutativity
Commutativity Axioms
Addition
∀ a, b ∈ R, a + b = b + a
Multiplication
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 6 / 14

27. Field Axioms: Commutativity
Commutativity Axioms
Addition
∀ a, b ∈ R, a + b = b + a
Multiplication
∀ a, b ∈ R, a · b = b · a
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 6 / 14

28. Field Axioms: DPMA
Distributive Property of Multiplication over Addition
∀ a, b, c ∈ R, c · (a + b) = c · a + c · b
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 7 / 14

29. Field Axioms: Existence of an Identity Element
Existence of an Identity Element
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 8 / 14

30. Field Axioms: Existence of an Identity Element
Existence of an Identity Element
Addition
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 8 / 14

31. Field Axioms: Existence of an Identity Element
Existence of an Identity Element
Addition
∃! 0 : a + 0 = a for a ∈ R.
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 8 / 14

32. Field Axioms: Existence of an Identity Element
Existence of an Identity Element
Addition
∃! 0 : a + 0 = a for a ∈ R.
Multiplication
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 8 / 14

33. Field Axioms: Existence of an Identity Element
Existence of an Identity Element
Addition
∃! 0 : a + 0 = a for a ∈ R.
Multiplication
∃! 1 : a · 1 = a and 1 · a = a for a ∈ R.
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 8 / 14

34. Field Axioms: Existence of an Inverse Element
Existence of an Inverse Element
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 9 / 14

35. Field Axioms: Existence of an Inverse Element
Existence of an Inverse Element
Addition
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 9 / 14

36. Field Axioms: Existence of an Inverse Element
Existence of an Inverse Element
Addition
∀ a ∈ R, ∃! (-a) : a + (−a) = 0
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 9 / 14

37. Field Axioms: Existence of an Inverse Element
Existence of an Inverse Element
Addition
∀ a ∈ R, ∃! (-a) : a + (−a) = 0
Multiplication
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 9 / 14

38. Field Axioms: Existence of an Inverse Element
Existence of an Inverse Element
Addition
∀ a ∈ R, ∃! (-a) : a + (−a) = 0
Multiplication
1 1
∀ a ∈ R − {0}, ∃! a : a· a =1
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 9 / 14

39. Equality Axioms
Equality Axioms
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 10 / 14

40. Equality Axioms
Equality Axioms
1 Reflexivity: ∀ a ∈ R : a = a
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 10 / 14

41. Equality Axioms
Equality Axioms
1 Reflexivity: ∀ a ∈ R : a = a
2 Symmetry: ∀ a, b ∈ R : a = b → b = a
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 10 / 14

42. Equality Axioms
Equality Axioms
1 Reflexivity: ∀ a ∈ R : a = a
2 Symmetry: ∀ a, b ∈ R : a = b → b = a
3 Transitivity: ∀ a, b, c ∈ R : a = b ∧ b = c → a = c
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 10 / 14

43. Equality Axioms
Equality Axioms
1 Reflexivity: ∀ a ∈ R : a = a
2 Symmetry: ∀ a, b ∈ R : a = b → b = a
3 Transitivity: ∀ a, b, c ∈ R : a = b ∧ b = c → a = c
4 Addition PE: ∀ a, b, c ∈ R : a = b → a + c = b + c
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 10 / 14

44. Equality Axioms
Equality Axioms
1 Reflexivity: ∀ a ∈ R : a = a
2 Symmetry: ∀ a, b ∈ R : a = b → b = a
3 Transitivity: ∀ a, b, c ∈ R : a = b ∧ b = c → a = c
4 Addition PE: ∀ a, b, c ∈ R : a = b → a + c = b + c
5 Multiplication PE: ∀ a, b, c ∈ R : a = b → a · c = b · c
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 10 / 14

45. Theorems from the Field and Equality Axioms
Cancellation for Addition: ∀ a, b, c ∈ R : a + c = b + c → a = c
a+c=b+c Given
a + c + (−c) = b + c + (−c) APE
a + (c + (−c)) = b + (c + (−c)) APA
a+0=b+0 ∃ additive inverses
a=b ∃ additive identity
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 11 / 14

46. Theorems from the Field and Equality Axioms
Prove the following theorems
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 12 / 14

47. Theorems from the Field and Equality Axioms
Prove the following theorems
Involution: ∀ a ∈ R : − (−a) = a
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 12 / 14

48. Theorems from the Field and Equality Axioms
Prove the following theorems
Involution: ∀ a ∈ R : − (−a) = a
Zero Property of Multiplication: ∀ a ∈ R : a · 0 = 0
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 12 / 14

49. Theorems from the Field and Equality Axioms
Prove the following theorems
Involution: ∀ a ∈ R : − (−a) = a
Zero Property of Multiplication: ∀ a ∈ R : a · 0 = 0
∀ a, b ∈ R : (−a) · b = −(ab)
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 12 / 14

50. Theorems from the Field and Equality Axioms
Prove the following theorems
Involution: ∀ a ∈ R : − (−a) = a
Zero Property of Multiplication: ∀ a ∈ R : a · 0 = 0
∀ a, b ∈ R : (−a) · b = −(ab)
∀ b ∈ R : (−1) · b = −b (Corollary of previous item)
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 12 / 14

51. Theorems from the Field and Equality Axioms
Prove the following theorems
Involution: ∀ a ∈ R : − (−a) = a
Zero Property of Multiplication: ∀ a ∈ R : a · 0 = 0
∀ a, b ∈ R : (−a) · b = −(ab)
∀ b ∈ R : (−1) · b = −b (Corollary of previous item)
(−1) · (−1) = 1 (Corollary of previous item)
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 12 / 14

52. Theorems from the Field and Equality Axioms
Prove the following theorems
Involution: ∀ a ∈ R : − (−a) = a
Zero Property of Multiplication: ∀ a ∈ R : a · 0 = 0
∀ a, b ∈ R : (−a) · b = −(ab)
∀ b ∈ R : (−1) · b = −b (Corollary of previous item)
(−1) · (−1) = 1 (Corollary of previous item)
∀ a, b ∈ R : (−a) · (−b) = a · b
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 12 / 14

53. Theorems from the Field and Equality Axioms
Prove the following theorems
Involution: ∀ a ∈ R : − (−a) = a
Zero Property of Multiplication: ∀ a ∈ R : a · 0 = 0
∀ a, b ∈ R : (−a) · b = −(ab)
∀ b ∈ R : (−1) · b = −b (Corollary of previous item)
(−1) · (−1) = 1 (Corollary of previous item)
∀ a, b ∈ R : (−a) · (−b) = a · b
∀ a, b ∈ R : − (a + b) = (−a) + (−b)
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 12 / 14

54. Theorems from the Field and Equality Axioms
Prove the following theorems
Involution: ∀ a ∈ R : − (−a) = a
Zero Property of Multiplication: ∀ a ∈ R : a · 0 = 0
∀ a, b ∈ R : (−a) · b = −(ab)
∀ b ∈ R : (−1) · b = −b (Corollary of previous item)
(−1) · (−1) = 1 (Corollary of previous item)
∀ a, b ∈ R : (−a) · (−b) = a · b
∀ a, b ∈ R : − (a + b) = (−a) + (−b)
Cancellation Law for Multiplication:
∀ a, b, c ∈ R, c = 0 : ac = bc → a = b
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 12 / 14

55. Theorems from the Field and Equality Axioms
Prove the following theorems
Involution: ∀ a ∈ R : − (−a) = a
Zero Property of Multiplication: ∀ a ∈ R : a · 0 = 0
∀ a, b ∈ R : (−a) · b = −(ab)
∀ b ∈ R : (−1) · b = −b (Corollary of previous item)
(−1) · (−1) = 1 (Corollary of previous item)
∀ a, b ∈ R : (−a) · (−b) = a · b
∀ a, b ∈ R : − (a + b) = (−a) + (−b)
Cancellation Law for Multiplication:
∀ a, b, c ∈ R, c = 0 : ac = bc → a = b
1
∀ a ∈ R, a = 0 : =a
(1/a)
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 12 / 14

56. Order Axioms
Order Axioms: Trichotomy
∀ a, b ∈ R, only one of the following is true:
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 13 / 14

57. Order Axioms
Order Axioms: Trichotomy
∀ a, b ∈ R, only one of the following is true:
1 a>b
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 13 / 14

58. Order Axioms
Order Axioms: Trichotomy
∀ a, b ∈ R, only one of the following is true:
1 a>b
2 a=b
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 13 / 14

59. Order Axioms
Order Axioms: Trichotomy
∀ a, b ∈ R, only one of the following is true:
1 a>b
2 a=b
3 a<b
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 13 / 14

60. Order Axioms
Order Axioms: Inequalities
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 14 / 14

61. Order Axioms
Order Axioms: Inequalities
1 Transitivity for Inequalities
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 14 / 14

62. Order Axioms
Order Axioms: Inequalities
1 Transitivity for Inequalities
∀ a, b, c ∈ R : a > b ∧ b > c → a > c
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 14 / 14

63. Order Axioms
Order Axioms: Inequalities
1 Transitivity for Inequalities
∀ a, b, c ∈ R : a > b ∧ b > c → a > c
2 Addition Property of Inequality
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 14 / 14

64. Order Axioms
Order Axioms: Inequalities
1 Transitivity for Inequalities
∀ a, b, c ∈ R : a > b ∧ b > c → a > c
2 Addition Property of Inequality
∀ a, b, c ∈ R : a > b → a + c > b + c
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 14 / 14

65. Order Axioms
Order Axioms: Inequalities
1 Transitivity for Inequalities
∀ a, b, c ∈ R : a > b ∧ b > c → a > c
2 Addition Property of Inequality
∀ a, b, c ∈ R : a > b → a + c > b + c
3 Multiplication Property of Inequality
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 14 / 14

66. Order Axioms
Order Axioms: Inequalities
1 Transitivity for Inequalities
∀ a, b, c ∈ R : a > b ∧ b > c → a > c
2 Addition Property of Inequality
∀ a, b, c ∈ R : a > b → a + c > b + c
3 Multiplication Property of Inequality
∀ a, b, c ∈ R, c > 0 : a > b → a · c > b · c
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 14 / 14

67. Theorems from the Order Axioms
Prove the following theorems
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 15 / 14

68. Theorems from the Order Axioms
Prove the following theorems
(4-1) R+ is closed under addition:
∀ a, b ∈ R : a > 0 ∧ b > 0 → a + b > 0
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 15 / 14

69. Theorems from the Order Axioms
Prove the following theorems
(4-1) R+ is closed under addition:
∀ a, b ∈ R : a > 0 ∧ b > 0 → a + b > 0
(4-2) R+ is closed under multiplication:
∀ a, b ∈ R : a > 0 ∧ b > 0 → a · b > 0
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 15 / 14

70. Theorems from the Order Axioms
Prove the following theorems
(4-1) R+ is closed under addition:
∀ a, b ∈ R : a > 0 ∧ b > 0 → a + b > 0
(4-2) R+ is closed under multiplication:
∀ a, b ∈ R : a > 0 ∧ b > 0 → a · b > 0
(4-3) ∀ a ∈ R : (a > 0 → −a < 0) ∧ (a < 0 → −a > 0)
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 15 / 14

71. Theorems from the Order Axioms
Prove the following theorems
(4-1) R+ is closed under addition:
∀ a, b ∈ R : a > 0 ∧ b > 0 → a + b > 0
(4-2) R+ is closed under multiplication:
∀ a, b ∈ R : a > 0 ∧ b > 0 → a · b > 0
(4-3) ∀ a ∈ R : (a > 0 → −a < 0) ∧ (a < 0 → −a > 0)
(4-4) ∀ a, b ∈ R : a > b → −b > −a
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 15 / 14

72. Theorems from the Order Axioms
Prove the following theorems
(4-1) R+ is closed under addition:
∀ a, b ∈ R : a > 0 ∧ b > 0 → a + b > 0
(4-2) R+ is closed under multiplication:
∀ a, b ∈ R : a > 0 ∧ b > 0 → a · b > 0
(4-3) ∀ a ∈ R : (a > 0 → −a < 0) ∧ (a < 0 → −a > 0)
(4-4) ∀ a, b ∈ R : a > b → −b > −a
(4-5) ∀ a ∈ R : (a2 = 0) ∨ (a2 > 0)
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 15 / 14

73. Theorems from the Order Axioms
Prove the following theorems
(4-1) R+ is closed under addition:
∀ a, b ∈ R : a > 0 ∧ b > 0 → a + b > 0
(4-2) R+ is closed under multiplication:
∀ a, b ∈ R : a > 0 ∧ b > 0 → a · b > 0
(4-3) ∀ a ∈ R : (a > 0 → −a < 0) ∧ (a < 0 → −a > 0)
(4-4) ∀ a, b ∈ R : a > b → −b > −a
(4-5) ∀ a ∈ R : (a2 = 0) ∨ (a2 > 0)
(4-6) 1 > 0
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 15 / 14

74. Theorems from the Order Axioms
Prove the following theorems
(4-1) R+ is closed under addition:
∀ a, b ∈ R : a > 0 ∧ b > 0 → a + b > 0
(4-2) R+ is closed under multiplication:
∀ a, b ∈ R : a > 0 ∧ b > 0 → a · b > 0
(4-3) ∀ a ∈ R : (a > 0 → −a < 0) ∧ (a < 0 → −a > 0)
(4-4) ∀ a, b ∈ R : a > b → −b > −a
(4-5) ∀ a ∈ R : (a2 = 0) ∨ (a2 > 0)
(4-6) 1 > 0
∀ a, b, c ∈ R : (a > b) ∧ (0 > c) → b · c > a · c
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 15 / 14

75. Theorems from the Order Axioms
Prove the following theorems
(4-1) R+ is closed under addition:
∀ a, b ∈ R : a > 0 ∧ b > 0 → a + b > 0
(4-2) R+ is closed under multiplication:
∀ a, b ∈ R : a > 0 ∧ b > 0 → a · b > 0
(4-3) ∀ a ∈ R : (a > 0 → −a < 0) ∧ (a < 0 → −a > 0)
(4-4) ∀ a, b ∈ R : a > b → −b > −a
(4-5) ∀ a ∈ R : (a2 = 0) ∨ (a2 > 0)
(4-6) 1 > 0
∀ a, b, c ∈ R : (a > b) ∧ (0 > c) → b · c > a · c
1
∀ a ∈ R: a > 0 → > 0
a
Mathematics 4 () Axioms on the Set of Real Numbers June 7, 2011 15 / 14