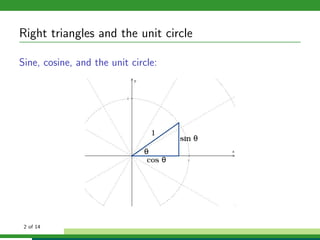
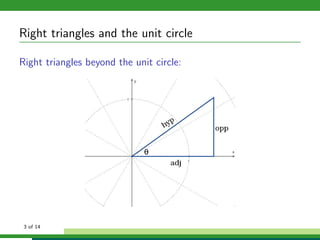
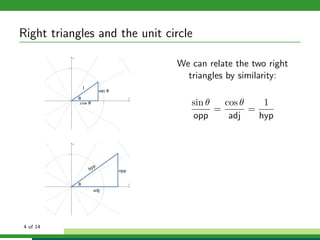
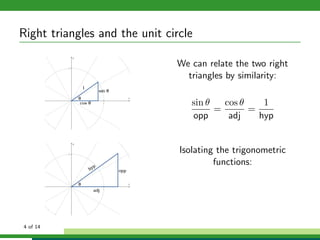
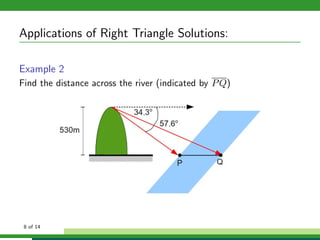
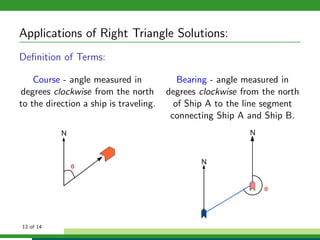
This document discusses solving right triangle problems using trigonometric functions like sine, cosine, and tangent. It provides examples of right triangles where certain sides or angles are given and asks the reader to solve for unknown values. Applications discussed include finding the length of a pole or distance across a river using right triangles defined by angles of elevation or depression. Bearings and courses of ships are also defined and used in an example of finding distance and bearings between two moving ships after a period of time.

1. Solving Right Triangle Problems
Mathematics 4
October 27, 2011
1 of 14

2. Right triangles and the unit circle
Sine, cosine, and the unit circle:
2 of 14

3. Right triangles and the unit circle
Right triangles beyond the unit circle:
3 of 14

4. Right triangles and the unit circle
We can relate the two right
triangles by similarity:
sin θ cos θ 1
= =
opp adj hyp
4 of 14

5. Right triangles and the unit circle
We can relate the two right
triangles by similarity:
sin θ cos θ 1
= =
opp adj hyp
Isolating the trigonometric
functions:
4 of 14

6. Right triangles and the unit circle
We can relate the two right
triangles by similarity:
sin θ cos θ 1
= =
opp adj hyp
Isolating the trigonometric
functions:
opp
sin θ =
hyp
4 of 14

7. Right triangles and the unit circle
We can relate the two right
triangles by similarity:
sin θ cos θ 1
= =
opp adj hyp
Isolating the trigonometric
functions:
adj
cos θ =
hyp
4 of 14

8. Right triangles and the unit circle
We can relate the two right
triangles by similarity:
sin θ cos θ 1
= =
opp adj hyp
Isolating the trigonometric
functions:
opp
tan θ =
adj
4 of 14

9. Solve the right triangles given the following parts:
1. α = 17o , a = 135
5 of 14

10. Solve the right triangles given the following parts:
1. α = 17o , a = 135 β = 73o , c = 461.7, b = 441.6
5 of 14

11. Solve the right triangles given the following parts:
1. α = 17o , a = 135 β = 73o , c = 461.7, b = 441.6
2. a = 64.5, b = 57.2
5 of 14

12. Solve the right triangles given the following parts:
1. α = 17o , a = 135 β = 73o , c = 461.7, b = 441.6
2. a = 64.5, b = 57.2 α = 48.4o , β = 41.6o , c = 86.2
5 of 14

13. Applications of Right Triangle Solutions:
Definition of terms:
Angle of Elevation Angle of Depression
6 of 14

14. Applications of Right Triangle Solutions:
Example 1
Find the length of the pole, and the distance of the pole from the
building.
7 of 14

15. Applications of Right Triangle Solutions:
Example 2
Find the distance across the river (indicated by P Q)
8 of 14

16. Applications of Right Triangle Solutions:
Example 3: The problem needs to be illustrated first
How high is a building whose horizontal shadow is 50
meters when the angle of elevation of the sun is 65
degrees?
9 of 14

17. Applications of Right Triangle Solutions:
Example 4
An 18-meter ladder leaning up against a building
makes a 70 degree angle with the ground. How far up
the building does the ladder touch?
10 of 14

18. Applications of Right Triangle Solutions:
Example 5
A 36-foot ladder is used to reach the top of a 28-foot
wall. If the ladder extends 2 feet past the top of the
wall, find its inclination to the horizontal.
11 of 14

19. Applications of Right Triangle Solutions:
Definition of Terms:
Course - angle measured in Bearing - angle measured in
degrees clockwise from the north degrees clockwise from the north
to the direction a ship is traveling. of Ship A to the line segment
connecting Ship A and Ship B.
12 of 14

20. Applications of Right Triangle Solutions:
Example 6
Two ships leave a port at the same time. The first
ship sails on a course of 25 degrees at 15 knots (1
knot = 1 mi/hr) while the second ship sails on a
course of 115 degrees at 20 knots. Find after two
hours (a) the distance between the ships, and (b) the
bearing from the first ship to the second and (c) the
bearing of the second ship to the first.
13 of 14

21. Any questions?
14 of 14