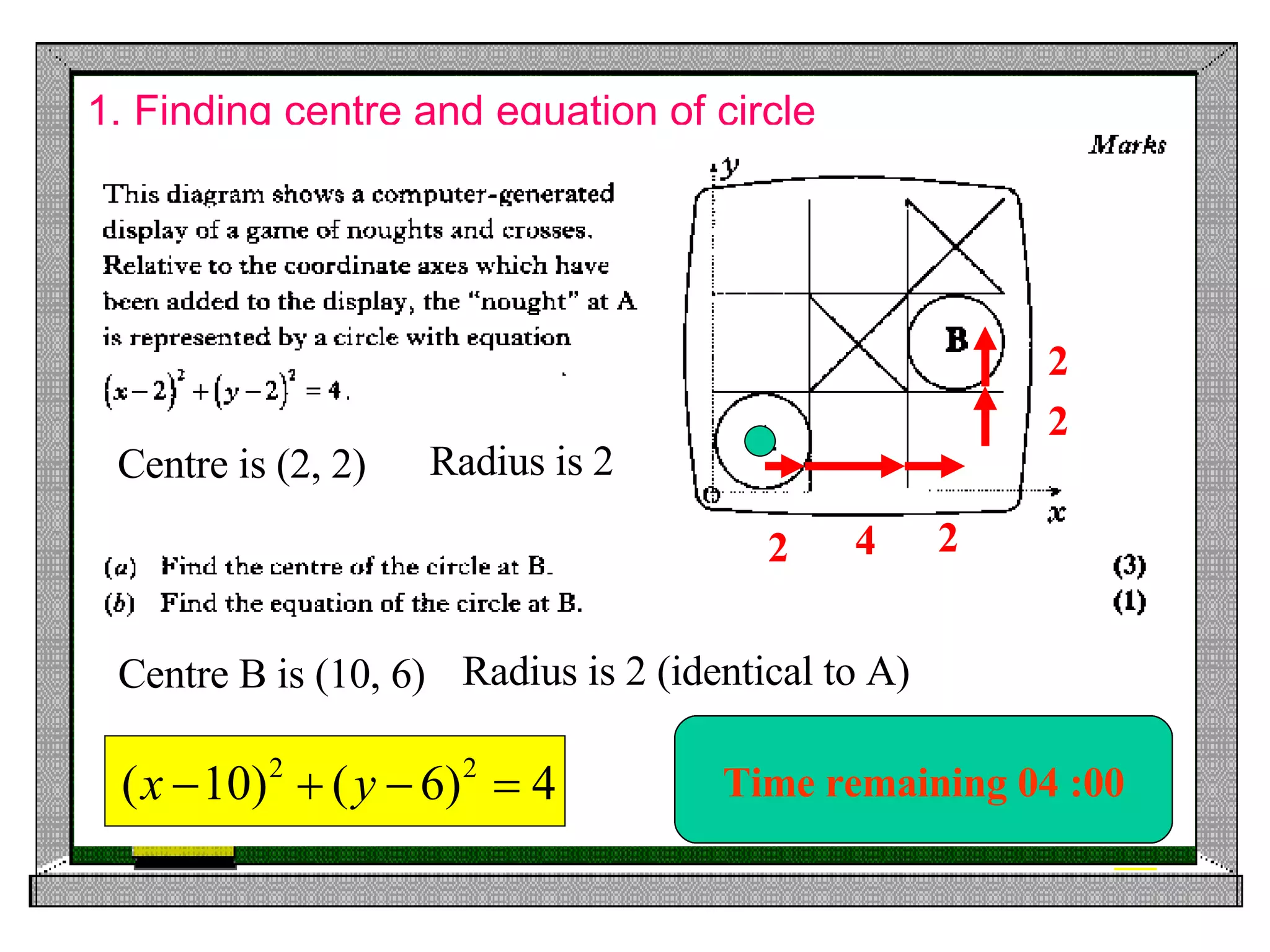
This document provides exam strategies and worked examples for solving circle geometry problems: 1) Finding the center and radius of a circle given its equation, and writing the equation of a circle given its center and radius. 2) Finding the equation of a tangent line to a circle at a given point. 3) Proving that a line is tangent to a circle by substituting the line equation into the circle equation. 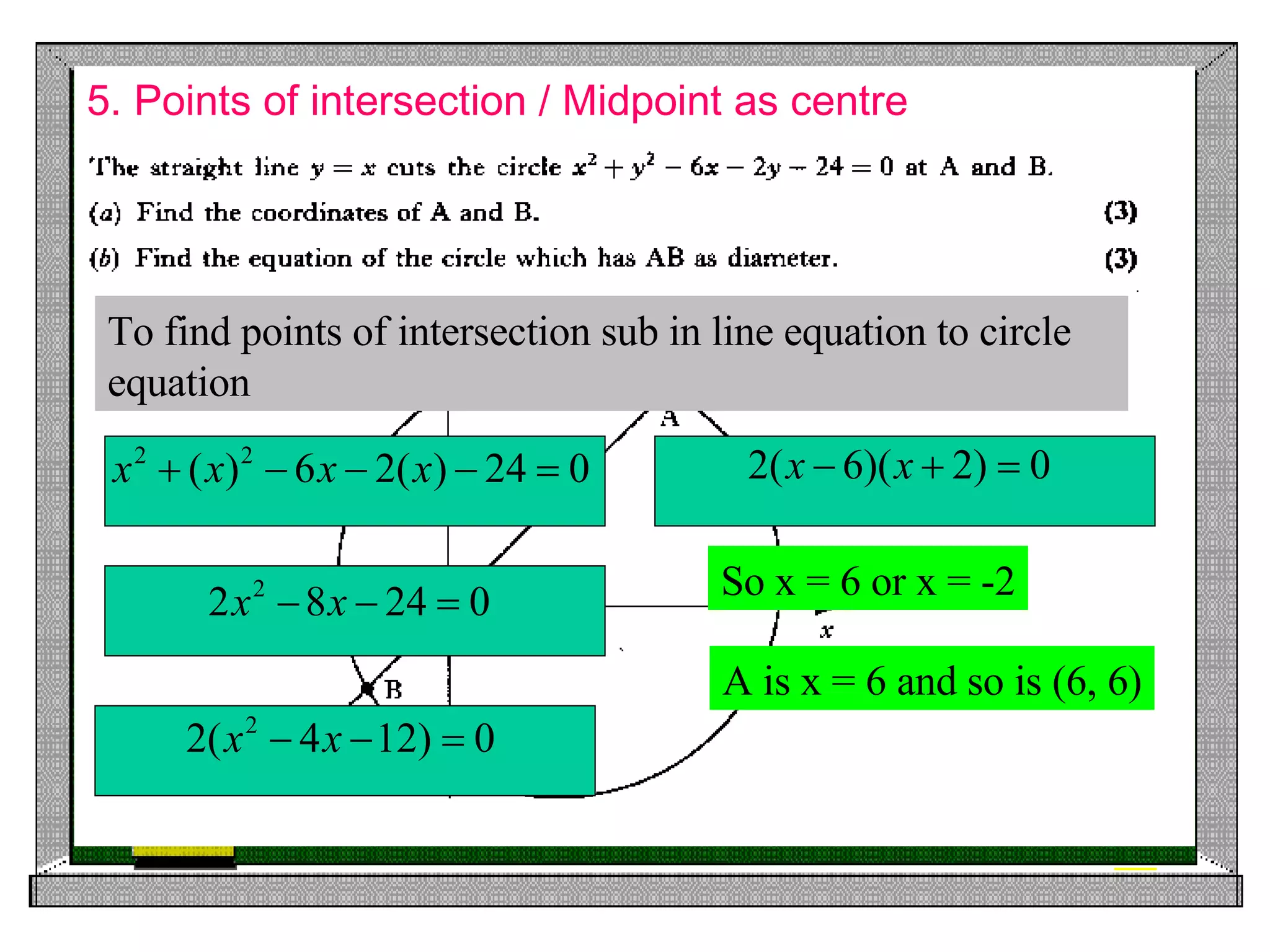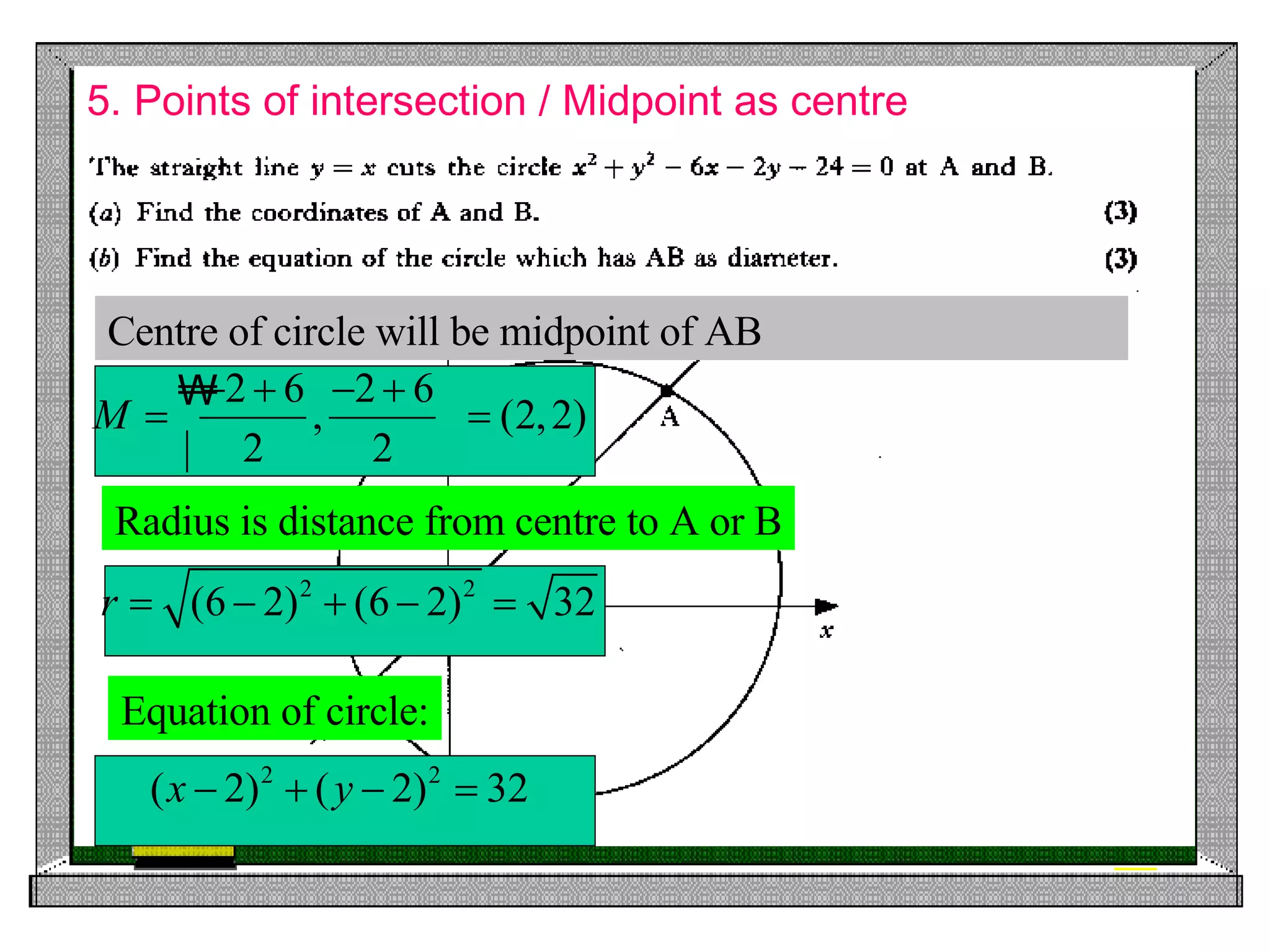4) Finding the points of intersection between a line and circle, and using the midpoint of a diameter as the circle's center. 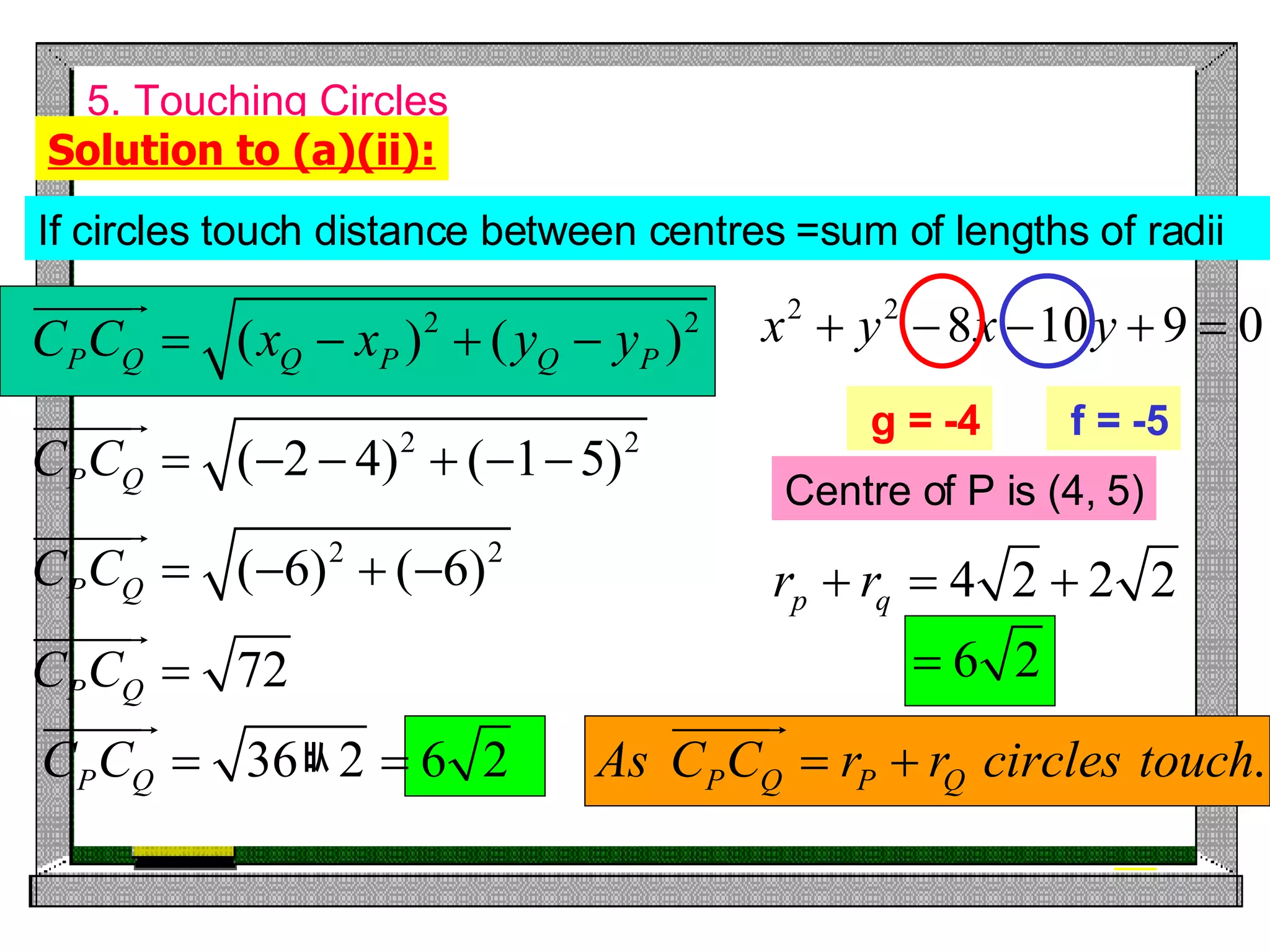5) Determining whether two circles touch based on the distance between their centers and the sums of their radii.

1. Exam Strategies Circles

2. What do you need to know? How to find centre and radius of circle Finding equation of circle : (x-a) 2 + (y-b) 2 = r 2 Equation of tangent to circle at given point Proving tangency Do circles touch? Points of intersection (line & circle) Common tangent Midpoint of diameter is centre of circle

3. 1. Finding centre and equation of circle Time remaining 00 :00 Time remaining 00 :05 Time remaining 00 :10 Time remaining 00 :20 Time remaining 00 :30 Time remaining 01 :00 Time remaining 02 :00 Centre is (2, 2) Radius is 2 2 4 2 2 2 Centre B is (10, 6) Radius is 2 (identical to A) Time remaining 03 :00 Time remaining 04 :00

4. 2. Radius of circle Time remaining 00 :00 Time remaining 00 :05 Time remaining 00 :10 Time remaining 00 :20 Time remaining 00 :30 Time remaining 01 :00 Time remaining 02 :00 Time remaining 03 :00 For circle radius must be positive so: 2g = -6 2f = 4 g = -3 f = 2

5. 3. Equation of tangent Time remaining 00 :00 Time remaining 00 :05 Time remaining 00 :10 Time remaining 00 :20 Time remaining 00 :30 Time remaining 01 :00 Time remaining 02 :00 Time remaining 03 :00 Time remaining 04 :00 Equation thru (3,4) Gradient of radius: Gradient of tangent:

6. 4. Proving tangency / Common tangents 8 Marks Show that the line x + 2y = 3 is a tangent to the circle (b) Show that this tangent is also a tangent to the circle with equation To prove tangency sub in equation of line into equation of circle and show b 2 – 4ac = 0.

7. 4. Proving tangency / Common tangents 8 Marks Show that the line x + 2y = 3 is a tangent to the circle (b) Show that this tangent is also a tangent to the circle with equation To prove tangency sub on equation of line into equation of circle and show b 2 – 4ac = 0.

8. 4. Proving tangency / Common tangents 8 Marks Show that the line x + 2y = 3 is a tangent to the circle (b) Show that this tangent is also a tangent to the circle with equation In part (b) do exactly the same!!!!!!

9. 5. Points of intersection / Midpoint as centre To find points of intersection sub in line equation to circle equation So x = 6 or x = -2 A is x = 6 and so is (6, 6)

10. 5. Points of intersection / Midpoint as centre Centre of circle will be midpoint of AB Radius is distance from centre to A or B Equation of circle:

11. 5. Touching Circles 4 Marks (a) (i) Show that the radius of circle P is (ii) Hence show that circles P and Q touch. Circle P has equation Circle Q has centre (-2, -1) and radius

12. 5. Touching Circles Solution to (a)(i): If given general form of circle’s equation remember 2g = -8 g = -4 2f = -10 f = -5

13. 5. Touching Circles Solution to (a)(ii): If circles touch distance between centres =sum of lengths of radii g = -4 f = -5 Centre of P is (4, 5)