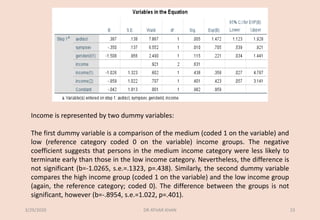
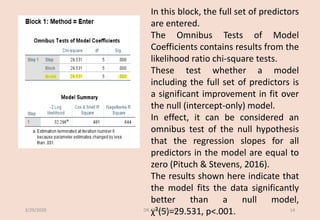
Binary logistic regression can be used to model the relationship between predictor variables and a binary dependent variable. The document discusses using logistic regression to predict the likelihood of clients terminating counseling early based on gender, income level, avoidance of disclosure, and symptom severity. The full model was statistically significant and correctly classified 84.4% of cases. Avoidance of disclosure and symptom severity significantly predicted early termination, while gender and income level were not significant predictors.

1. BINARY LOGISTIC REGRESSION
Dr. Athar Khan
matharm@yahoo.com
3/29/2020 DR ATHAR KHAN 1

2. Binary logistic regression (BLR) is utilized when a
researcher desires to model the relationship between one
or more predictor variables and a binary dependent
variable.
Fundamentally, the researcher is addressing the question:
“What is the probability that a given case falls into one of
two categories on the dependent variable, given the
predictors in the model?”
3/29/2020 DR ATHAR KHAN 2

3. Scenario:
In this example, we are attempting to model the likelihood of early
termination from counseling in a sample of n=45 clients at a
community mental health center.
The dependent variable in the model is 'terminate' (coded
1=terminated early, 0=did not terminate early), where the “did
not terminate” group is the reference (baseline) category and the
“terminated early” group is the target category.
3/29/2020 DR ATHAR KHAN 3

4. Scenario:
Two predictors in the model are categorical:
Gender identification ('genderid', coded 0=identified as male,
1=identified as female). The reference category for ‘genderid’ is
male identification
‘Income' (ordinal variable, coded 1=low, 2=medium, 3=high). The
reference category for ‘income’ is the low income group.
Finally, two predictors are assumed continuous in the model:
avoidance of disclosure ('avdisc') and symptom severity
('sympsev’).
3/29/2020 DR ATHAR KHAN 4

7. Categorical predictor variables →Click the Categorical tab →Move
‘income’ over to the right →Set the ‘contrast’ to Indicator →Click on
‘first’ to make the low income group the reference category →Click
the ‘change’ button.

8. Reference category to ‘First’.
3/29/2020 DR ATHAR KHAN 8

9. 3/29/2020 DR ATHAR KHAN 9

10. Click on the Option tab →Check Classification Plots, the Hosmer-
Lemeshow goodness of fit test (although it is not highly
recommended), and confidence intervals for the odds ratios.3/29/2020 DR ATHAR KHAN 10

11. The output is presented in
blocks.
Block 0 contains the results from
a null (i.e., intercept-only) model.
3/29/2020 DR ATHAR KHAN 11

12. The first step, called Step 0, includes no predictors and just the
intercept. Often, this model is not interesting to researchers.
d. Observed – This indicates the number of 0’s and 1’s that are observed in
the dependent variable.
e. Predicted – In this null model, SPSS has predicted that all cases are 0 on
the dependent variable.
f. Overall Percentage – This gives the percent of cases for which the
dependent variables was correctly predicted given the model. In this part
of the output, this is the null model. 73.5 = 147/200.
g. B – This is the coefficient for the constant (also called the “intercept”) in
the null model.
h. S.E. – This is the standard error around the coefficient for the constant.
i. Wald and Sig. – This is the Wald chi-square test that tests the null
hypothesis that the constant equals 0. This hypothesis is rejected because
the p-value (listed in the column called “Sig.”) is smaller than the critical p-
value of .05 (or .01). Hence, we conclude that the constant is not 0.
Usually, this finding is not of interest to researchers.3/29/2020 DR ATHAR KHAN 12

13. j. df – This is the degrees of freedom for the Wald chi-square test. There is only one
degree of freedom because there is only one predictor in the model, namely the constant.
k. Exp(B) – This is the exponentiation of the B coefficient, which is an odds ratio. This
value is given by default because odds ratios can be easier to interpret than the
coefficient, which is in log-odds units. This is the odds: 53/147 = .361.
l. Score and Sig. – This is a Score test that is used to predict whether or not an
independent variable would be significant in the model. Looking at the p-values (located
in the column labeled “Sig.”), we can see that each of the predictors would be statistically
significant except the first dummy for ses.
m. df – This column lists the degrees of freedom for each variable. Each variable to be
entered into the model, e.g., read, science, ses(1) and ses(2), has one degree of freedom,
which leads to the total of four shown at the bottom of the column. The variable ses is
listed here only to show that if the dummy variables that represent ses were tested
simultaneously, the variable ses would be statistically significant.
n. Overall Statistics – This shows the result of including all of the predictors into the
model.
3/29/2020 DR ATHAR KHAN 13

14. In this block, the full set of predictors
are entered.
The Omnibus Tests of Model
Coefficients contains results from the
likelihood ratio chi-square tests.
These test whether a model
including the full set of predictors is
a significant improvement in fit over
the null (intercept-only) model.
In effect, it can be considered an
omnibus test of the null hypothesis
that the regression slopes for all
predictors in the model are equal to
zero (Pituch & Stevens, 2016).
The results shown here indicate that
the model fits the data significantly
better than a null model,
χ²(5)=29.531, p<.001.3/29/2020 DR ATHAR KHAN 14

15. The Model Summary table contains the -2 log likelihood and two “pseudo-R-square”
measures. The pseudo-R-squares are interpreted as analogous to R-square (being mindful
that they are not computed in the same fashion as in OLS regression). In general, there is
no strong guidance in the literature on how these should be used or interpreted (Lomax &
Hahs-Vaugn, 2012; Osborne, 2015; Pituch & Stevens, 2016; Smith & McKenna, 2013). Smith
and McKenna (2013) further noted that “the most commonly used pseudo R2 indices (e.g.,
McFadden’s index, Cox-Snell index with or without Nagelkerke correction) yield lower
estimates than their OLS R2 counterparts”, suggesting the possibility that “unique” and
“less stringent” (p. 24-25) guidelines by used when interpreting these indices.
The -2*Log likelihood (also referred to as “model deviance” (Pituch & Stevens, 2016) is
most useful for comparing competing models, particularly because it is distributed as chi-
square (Field, 2018).
3/29/2020 DR ATHAR KHAN 15

16. Given the limitations of “pseudo-R-square” as indices of model fit, some authors
have proposed an alternative approach to computing R-square based on logistic
regression that is more akin to the R-square in OLS regression. Tabachnick and
Fidell (2013) and Lomax and Hahs-Vaughn (2012) suggest that one can compute
an R-square value by (a) correlating group membership on the dependent
variable with the predicted probability associated with (target) group
membership (effectively a point-biserial correlation) and (b) squaring that
correlation. As a demonstration with the current data:
3/29/2020 DR ATHAR KHAN 16

17. r=.729
R-square=.531
(as can be seen, these two variables
share considerable variation)
3/29/2020 DR ATHAR KHAN 17

18. The Hosmer & Lemeshow test is another test that can be used
to evaluate global fit. A non-significant test result (as seen here;
p=.97) is an indicator of good model fit.
3/29/2020 DR ATHAR KHAN 18

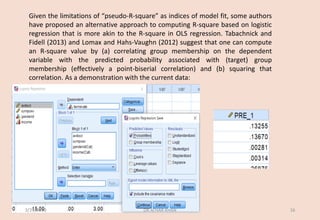
19. The classification table provides the frequencies and percentages reflecting the degree
to which the model correctly and incorrectly predicts category membership on the
dependent variable. We see that 100%*23/(23+2) = 92% of cases that were observed
not terminate early were correctly predicted (by the model) to not terminate early. Of
the 20 cases observed to terminate early, 100%*15/(5+15) = 75% were correctly
predicted by the model to terminate early. [As you can see, sensitivity refers to
accuracy of the model in predicting target group membership, whereas specificity
refers to the accuracy of a model to predict non-target group membership.] The overall
classification accuracy based on the model was 84.4%.
3/29/2020 DR ATHAR KHAN 19

20. The ‘Estimate’ column contains the regression coefficients. For each predictor, the
regression slope is the predicted change in the log odds of falling into the target group (as
compared to the reference group on the dependent variable) per one unit increase on
the predictor (controlling for the remaining predictors). [Note: A common misconception
is that the regression coefficient indicates the predicted change in probability of target
group membership per unit increase on the predictor – i.e., p(Y=1|X’s). This is WRONG!
The coefficient is the predicted change in log odds per unit increase on the predictor].
Nevertheless, you can generally interpret a positive regression coefficient as indicating
the probability (loosely speaking) of falling into the target group increases as a result of
increases on the predictor variable; and that a negative coefficient indicates that the
probability (again, loosely speaking) of target membership decreases with increases on
the predictor. If the regression coefficient = 0, this can be taken to indicate changes in the
probability of being in the target group as scores on the predictor increase.
3/29/2020 DR ATHAR KHAN 20

21. The Odds Ratio (OR) column contains values that are interpreted as the multiplicative
change in odds for every one unit increase on a predictor. In general, an odds ratio (OR) >
1 indicates that as scores on the predictor increase, there is an increasing probability of
the case falling into the target group on the dependent variable. An odds ratio (OR) < 1
can be interpreted as decreasing probability of being in the target group as scores on the
predictor increase. If the OR=1, then this indicates no change in the probability of being
in the target group as scores on the predictor change.
The 95% confidence interval for the Odds ratio can also be used to test the observed OR
to determine if it is significantly different from the null OR of 1.0. If 1.0 falls between the
lower and upper bound for a given interval, then the computed odds ratio is not
significantly different from 1.0 (indicating no change as a function of the predictor).
3/29/2020 DR ATHAR KHAN 21

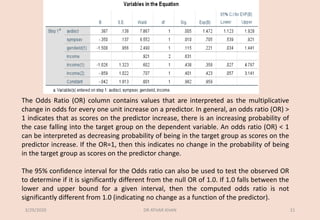
22. ▪ Avoidance of disclosure is a positive and significant (b=.3866, s.e.=.138, p=.005)
predictor of the probability of early termination, with the OR indicating that for
every one unit increase on this predictor the odds of early termination change by a
factor of 1.472 (meaning the odds are increasing).
▪ Symptom severity is a negative and significant (b=-.3496, s.e.=.137, p=.010)
predictor of the probability of early termination. The OR indicates that for every
one unit increment on the predictor, the odds of terminating increase by a factor of
.705 (meaning that the odds are decreasing).
▪ Genderid is a non-significant predictor of early termination (b=-1.5079, s.e.=.0956,
p=.115). [Had the predictor been significant, then the negative coefficient would be
taken as an indicator that females (coded 1) are less likely to terminate early than
males.]
3/29/2020 DR ATHAR KHAN 22

23. Income is represented by two dummy variables:
The first dummy variable is a comparison of the medium (coded 1 on the variable) and
low (reference category coded 0 on the variable) income groups. The negative
coefficient suggests that persons in the medium income category were less likely to
terminate early than those in the low income category. Nevertheless, the difference is
not significant (b=-1.0265, s.e.=.1323, p=.438). Similarly, the second dummy variable
compares the high income group (coded 1 on the variable) and the low income group
(again, the reference category; coded 0). The difference between the groups is not
significant, however (b=-.8954, s.e.=1.022, p=.401).
3/29/2020 DR ATHAR KHAN 23

24. Thanks for attending!
3/29/2020 DR ATHAR KHAN 24