This document provides an overview of key concepts related to work, energy, and power including: - The definitions and relationships between work, kinetic energy, gravitational potential energy, and elastic potential energy. - Conservative and non-conservative forces. - How to calculate work done by non-conservative forces. - The work-energy theorem and the law of conservation of energy. - The definition of power as the rate of doing work.

1. Corinne Goldstein, Ali Lubin, Bridget Miller, and Stephen Desilets present…

2. In association with DreamWORKS studios…

3. A Chapter 6 Production…

4. DO WORK!

5. … And Energy

6. What’s this all about?

7. Well, let’s look at the terms…

8. Work – Measured in Joules Energy – Also measured in Joules Spring Constant – Measured in Newton/meters Power – Measure in Watts

9. Well Work and Energy are both measured in Joules. Are they the same thing?

10. NO

11. Work (W) Work is the Transfer of Energy, or more simply put, Force exerted over a Distance W = Fdcos Ө F = Magnitude of Force (Newtons) d = Magnitude of Displacement Ө = Angle between Force and Displacement

12. So 1 Joule = 1 Newton x 1 Meter

13. And if someone walks down a horizontal road… Work is done by that person… But the work done by gravitational force is zero since the displacement is perpendicular to the direction of the force

14. HOWEVER…

15. Energy of a body is its Capacity to do Work

16. Energy There’s 3 Types!

17. Kinetic Energy (KE or K) The Energy of Motion KE = ½ mv ² m = mass of the object v = velocity of the object

18. Gravitational Potential Energy The stored energy an object has due to its position above earth’s surface PE = mgh m = mass of the object g = acceleration of gravity h = height of the object relative to earth (or some other zero level)

19. Elastic Potential Energy (PE s ) Energy a Spring has by virtue of being stretched or compressed PE s = ½ kx ² k = Spring Constant – Measures the strength of the spring in N/m x = Distance the spring is stretched or compressed

20. Say, are Work and Energy related?

21. YES

22. Work exerted on an object is equal to the difference between an object’s initial and final Energies.

23. So…

24. W KE = KE – KE 0 = mv ² - ½ mv 0 ² W gravity = PE – PE 0 = mgh – mgh 0 or mg(h-h 0 ) W PE s = PE s – PE s0 = ½ kx² - ½ kx 0 ²

25. One of those equations even has its own theorem!

26. Can you guess which one?

27. Work-Energy Theorem WKE = KE – KE0 = mv ² - ½ mv0² Or in English terms… The work done by an object by an outside force is equal to the difference between the object’s final and initial kinetic energies

28. So have I mastered the Force?

29. Not yet. Much to learn there still is, Young Padawan.

30. Like the difference between Conservative Forces and Nonconservative Forces

31. Conservative Forces Force that exerts the same amount of force on an object moving between two points, no matter what path the object takes Types: Gravitational Potential Energy Elastic Spring Force Electric Force

32. What’s all that Mumbo Jumbo mean, though?

33. Let’s think about it.

34. Take the W gravity for example… The equation is W gravity = mg(h-h 0 ) So if an object falls 50 meters, the work exerted on the object by gravity won’t change whether the object fall straight down or falls on an angle. All that matters is the initial and final heights.

35. Well then what’s a Non-Conservative Force?

36. Non-Conservative Force Force that exerts a different amount of work on an object moving between two points depending on what path the object takes Types: Static and Kinetic Frictional Forces Air Resistance Tension Normal Forces Propulsion Force of a Rocket

37. Okay, well what if I want to calculate the work due to non-conservative forces acting on an object?

38. Good Question!

39. Effectively, you can calculate the work exerted on an object by non-conservative forces by… finding the difference between the initial and final energies due to conservative forces acting on an object. The difference is the work due to non-conservative forces that acts on the object

40. So… Wnc = Δ KE + Δ PE + Δ PE s or W nc = ( ½mv² - ½ mv 0 ²) + (mgh – mgh 0 ) + (½ kx² - ½kx 0 ²) ( Δ means change)

41. Let’s Conserve Energy!

42. Mechanical Energy (ME or E) of and object is the sum of the kinetic and potential energies of that object E = KE + PE

43. When the net work exerted on a moving object by non-conservative forces is zero, the total mechanical energy of that object remains constant…

44. … In this case, KE and PE can be transformed into one another as the object moves.

45. Cool Beans!

46. If there are no non-conservative forces acting on the object, then the initial and final total energies should be equal

47. So… W nc = ( ½mv² + mgh + ½kx²) - (½mv 0 ² + mgh 0 + ½kx 0 ²) or ½mv² + mgh + ½kx² = ½mv 0 ² + mgh 0 + ½kx 0 ²

48. I GOT THE POWER!

49. Power The Rate at which Work is done P = W/t or P = Fv or P = (Fdcos Ө )/t Measured in Watts (W)

50. So… 1 Watt = 1 Joule per second

51. We’re Almost Done!

52. Hey, remember how Work = Force x Distance?

53. Well, if you plot Force on one axis of a graph and Distance on the other, then you can calculate the Work exerted by finding the area under the line.

54. Just like Area = Length x Width, Work = Force x Distance

55. Time to Practice!

56. Find the work exerted on a suitcase if the suitcase is being pulled with a force of 16.0 N at a 56.0 º angle to the floor and the displacement of the suitcase is 63.0 cm.

57. W = Fdcos Ө W = (16.0N)(0.63m)(cos56.0º)

58. Degree Mode is your friend.

59. W = 5.64 J

60. An archer pulls a bowstring back a distance of 0.470m and then releases the arrow. The bow and string act like a spring whose spring constant is 425 N/m. What is the elastic potential energy of the system?

61. PE = ½kx² PE = ½(425N/m)(0.470m)² PE = 46.9 J

62. A motorcyclist is trying to leap across a canyon by driving horizontally off the cliff at a speed of 38.0 m/s. Ignoring air resistance, find the speed at which the motorcycle strikes the ground on the other side. The motorcycle starts at a height of 70.0m and will end at a height of 35.0m.

63. ½ mv ² + mgh = ½mv 0 ² + mgh 0 (mass cancels out) ½v ² + (9.8m/s²)(35.0m) = ½(38.0m/s) ² + (9.8m/s²)(70.0m) V = 46.2 m/s

64. A 0.20kg rocket is launched from rest. It takes a roundabout route until it reaches a height of 29m above its starting point. In the process, 425J of work is done on the rocket by non-conservative forces (the burning propellant). Ignoring air resistance and the mass lost due to the burning of the fuel, find the speed of the rocket when it is 29 m above its starting point.

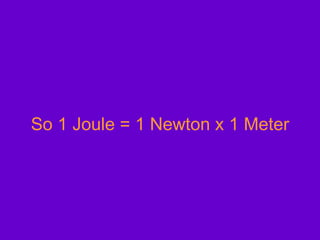
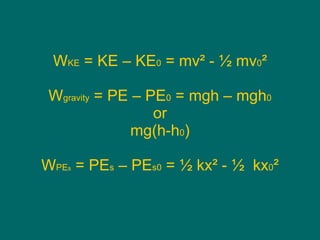
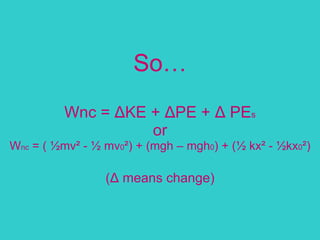
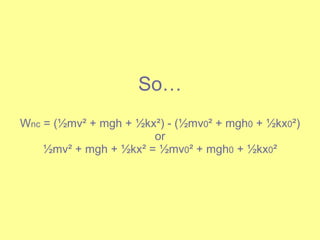
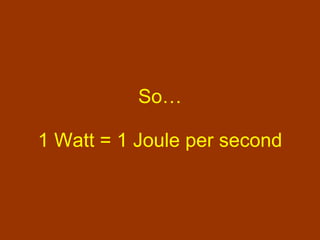
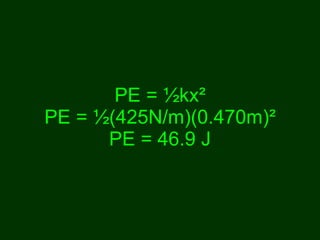
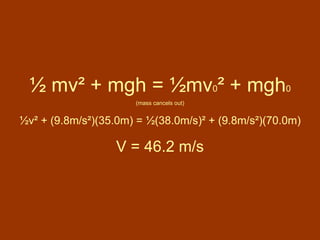
65. W nc = ½mv ² + mgh – ( ½mv 0 ² + mgh 0 ) 425J = [½(0.20kg)v ² + (0.20kg)(9.8m/s²)(27m)] – [ ½(0.20kg)(0m/s) ² + (0.20kg)(9.8m/s²)(0m)] V = 61 m/s

66. A car starts from rest and accelerates in a positive direction. The car has a mass of 1.10 x 10 ³kg and accelerates at +4.60m/s² for 5.00s. Determine the average power generated by the force that moves the car.

67. V = v 0 + at v = 0m/s + (4.6m/s)(5.00s) v = 23 m/s P = Fv P = mav P = (1.10 x 10 ³kg)(4.6m/s²)(23m/s) P = 1.16 x 10^5 W

68. Th-Th-That’s All Folks!

69. It’s Physics-tastic!