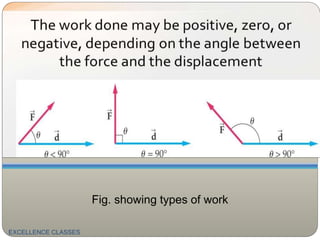
Work is defined as the product of the force applied and the displacement in the direction of the force. Work can be positive, negative, or zero depending on the angle between the force and displacement vectors. The SI unit of work is the joule. Power is defined as the rate of doing work, or the amount of work done per unit time. The SI unit of power is the watt. Energy is the ability to do work and exists in various forms including kinetic energy, potential energy, and mechanical energy. The law of conservation of energy states that the total energy in an isolated system remains constant. It can be transformed from one form to another but cannot be created or destroyed.

1. PREPARED BY :
Mr. KEYUR MARADIYA
WORK, POWER & ENERGY

2. WORK
 The work done by a constant
force is defined as product of
force in the direction of the
displacement and the
magnitude of the
displacement.
 W = F.S.Cos
ᶿ
Where, F = constant force,
S =displacement,
Work is a scaler quantity.
EXCELLENCE CLASSES

3. Conditions required for work to be
done:
 The object must undergo a displacement.
 F must have a non zero component , in the direction of
S , if the displacement is in the direction of force, then
work done is given by
W = F x S
i.e. Work = Force x displacement of point of
application of force in the
direction of force.
EXCELLENCE CLASSES

4. Types of Work.
Depending upon the angle formed between the force and
displacement work ca be either.
 Positive work - When 0o <= θ <=90o, work done is positive.
 When a body is falling down, the force of gravitation is acting in
the downward direction. The displacement is also in the
downward direction. Thus the work done by the gravitational
force on the body is positive.
 Negative work – When 90o <= θ <= 180o , work done is
negative.
 Consider the body being lifted in the upward direction. In this
case, the force of gravity is acting in the downward direction.
But, the displacement of the body is in the upward direction.
Since the angle between the force and displacement is 180o,
the work done by the gravitational force on the body is negative.
EXCELLENCE CLASSES

5.  Similarly, frictional force is always opposing the relative motion
of the body. When a body is dragged along a rough surface, the
frictional force will be acting in the direction opposite to the
displacement. The angle between the frictional force and the
displacement of the body will be 180o. Thus, the work done by
the frictional force will be negative.
 Zero work – when θ = 90, work done is zero.
 When we hold an object and walk, the force acts in downward
direction whereas displacement acts in forward direction.
 Work done by centripetal force.
EXCELLENCE CLASSES

6. Fig. showing types of work
EXCELLENCE CLASSES

7. UNITS OF WORK
EXCELLENCE CLASSES
 S.I unit – Joule where 1 J = 1 N x 1 m.
 CGS unit – erg where 1 erg = 1 dyne x 1cm.
 Definition of 1 Joule – Work is said to be one joule if a
force of one newton displaces a body through a distance
of 1m in its own direction.
 Definition of 1 erg – Work is said to be one erg if a force
of one dyne displaces a body through a distance of 1cm
in its own direction.

8. Relation between SI and CGS units
EXCELLENCE CLASSES
 S.I. unit of work is Joule (J) or Nm.
C.G.S unit of work is erg or dyne cm.
where,
 1N=105 dyne and 1m=100 cm
∴ 1 J = 1 Nm = 105 dyne × 102 cm
∴ 1 J = 107 erg

9. Work done under various situations
EXCELLENCE CLASSES
 Vertical climb in a lift – In this case the displacement of
the body is in the same direction as applied force but
against the force of gravity, so work has to be done
against gravity.
∴ W = F S cos θ
Here displcement and force are in the same direction so θ
= 0
∴ W = F S cos0 = F S (as cos 0 = 1 )
But F = mg and if the lift moves through height ‘h’ then,
W =mgh
This is WD against gravity when body a moves in a lift.

10. EXCELLENCE CLASSES
 Climbing stairs - Consider a body of mass ‘m’ climbing a
staircase of height ‘h’. Suppose there are ‘n’ steps of
height h1 each. During his climb of each steps the body
exerts an upward force equal to his weight mg in
climbing a vertical distance h1. Thus the displacement is
in the direction of applied force. Therefore WD in
climbing one step ,
 W1 = F S = mgh1
∴ WD in climbing n steps, W = W1 x n = mgh1n
But nh1 = h , total height of staircase
∴ W = mgh

11. POWER
EXCELLENCE CLASSES
 Power is defined as rate of doing work.
 It is measured as the amount of workdone in one
second.
 Power = Work done / Time
= W / t = F.S / t
or Power = F x v ( since s / t = v ; velocity)
Power = Force x Velocity
 Power is a Scaler quantity.

12. EXCELLENCE CLASSES
 SI unit of Power is joule per sec also called Watt.
 CGS unit of power is erg per sec .
 If 1 J of work is done in one second then the power is
said to be one Watt. i.e 1 W = 1 Js-1
 Relation between SI and CGS units
1J = 107 erg
∴ 1J/s = 107 erg / s
∴ 1 W = 107 erg / s.
 Other units of power :
1hp = 746 W 1 MW = 106 W 1 GW = 109 W
 The power is said to be 1 hp if an average horse can lift
550 pound through a distance of 1 foot in 1 sec

13. ENERGY
EXCELLENCE CLASSES
 Energy is the capacity of a body to do work.
 SI unit is Joule
 CGS unit is erg.
 Bigger units of energy are watt-hour (Wh)and kilowatt-
hour (kWh).
 1 kilowatt-hour is defined as energy consumed by an
agent of 1kW power in one hour.
1 kWh = 3.6 x 106 J
 In nuclear physics energy is measured in electronvolt
(eV).
 One electronvolt is the energy gained by an electron
when accelerated through a potential difference of 1 volt.
 1eV = 1.6 x 10-19 J 1MeV = 1.6 x 10-13 J

14. MECHANICAL ENERGY
EXCELLENCE CLASSES

15. DERIVATION for K.E. for a body starting from Rest
Consider a body of mass ‘m’ initially lying at rest, i.e. u=0 on a perfectly
frictionless surface. Let a constant force F be acting on the body such that it
produces an acceleration ‘a’ . Let the body possess a velocity ‘V’ after
undergoing a displacement ‘S’.
Also WD by the force in displacing the body through a distance S is given by,
EXCELLENCE CLASSES

16. Derivation for KE for a body possessing some
initial velocity U
EXCELLENCE CLASSES
 Consider a body of mass ‘m’ initially lying at rest, i.e. u=0 on a
perfectly frictionless surface. Let a constant force F be acting
on the body such that it produces an acceleration ‘a’ . Let the
velocity of the body change to ‘V’ after undergoing a
displacement ‘S’, then by equation of motion v2 – u2 = 2aS we
get,
S= (v2 – u2 )/2a
 Also WD by the force in displacing the body through a distance
S is given by, W = FS
∴ W = FS = ma x S = ma x (v2 – u2 )/2a
W = ½ mv2 - ½ mu2
Thus WD = Increase in KE .
This is called WORK ENERGY PRINCIPLE

17. Relation Between KE and Momentum
EXCELLENCE CLASSES

18. Forms of Kinetic Energy
EXCELLENCE CLASSES
 Translational K.E. – Straight line motion.
e.g free falling body.
 Rotational K.E – Spinning motion.
e.g spinning top, rotating fan.
 Vibrational K.E – Vibrating motion.
e.g simple pendulum.

19. Types o Potential Energy
EXCELLENCE CLASSES
 Gravitational potential energy - It is the energy stored in an
object as the result of its vertical position or height. The
energy is stored as the result of the gravitational attraction of
the Earth for the object.
 Elastic potential energy -Elastic potential energy is Potential
energy stored as a result of deformation of an elastic object,
such as the stretching of a spring. It is equal to the work done
to stretch the spring.
 Electrostatic potential energy -A pair of charges will always
have some potential energy because if they are released from
rest, they will either start moving towards (if the charges are
different) or away (if the charges are the same) from each
other. Electrostatic potential energy is specifically the
energy associated with a set of charges arranged in a certain
configuration.

20. Gravitational Potential Energy
Consider the body of mass m lying on the
surface of the earth. Let this body be moved
the through a distance h away from the surface
vertically upward as shown in fig. To do so
work will be done against the gravitational
force of attraction acting on the body which is
equal to weight mg. This workdone is given by
the expression,
W = FS = mgh
This work is stored in the body as its
gravitational potential energy,
Therefore we have , U = mgh
EXCELLENCE CLASSES

21. Law of Conservation of Energy
EXCELLENCE CLASSES
 The law of conservation of energy states that energy can
neither be created nor be destroyed. Although, it may be
transformed from one form to another.
 According to this principle, the total mechanical energy remains
constant under the action of conservative forces
E = K + U
For a Free falling body
 Considering the potential energy at the surface of the earth to
be zero. Let us see an example of a fruit falling from a tree.
 Consider a point A, which is at some height ‘H’ from the ground
on the tree, the velocity of the fruit is zero hence potential
energy is maximum there.
 E = K = U = 0 + mgH = mgH ---------------(1)

22. EXCELLENCE CLASSES
 When the fruit is falling, its potential energy is decreasing and
kinetic energy is increasing.
 At point B, which is near the bottom of the tree, the fruit is
falling freely under gravity and is at a height X from the
ground, and it has speed as it reaches point B. So, at this
point, it will have both kinetic and potential energy.
 E = K.E + P.E
P.E = mgx
 According to third equation of motion, v2 – u2 = 2aS
We get v2 – 0= 2gx i .e v2 = 2gx
∴ K = ½ mv2 = ½ m(2gx) = mgx
And U = mg(h-x)
Hence at point B,
E =K + U = mgx + mg (h - x) = mgh ----------- (2)

23. EXCELLENCE CLASSES
 On reaching point C suppose the ball covers a distance
h. Let v be the velocity at point c just before it touches
the ground .Then by equation of motion,
v2 – u2 = 2aS we have v2 – 0 = 2gh
∴ K = ½ mv2 = ½ m(2gh) = mgh
& U =0
∴ Total energy at C is,
E = K + U= mgh --------------(3)
∴ From (1) (2) & (3) it is clear that the total mechanical
energy of a freely falling body remains constant.

24. Law of Conservation of Energy for
Simple Pendulum
EXCELLENCE CLASSES