SF
Uploaded bySimon Foo
PDF, PPTX3,484 views

Chapter 2 basic structure concepts

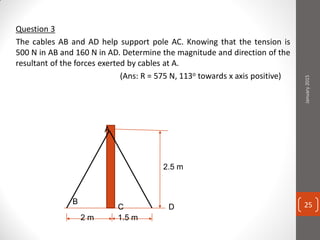
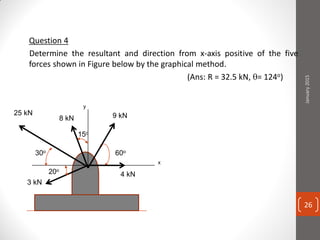
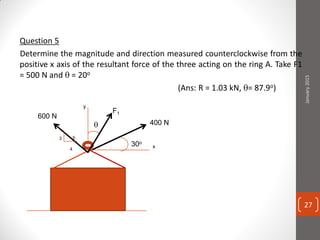
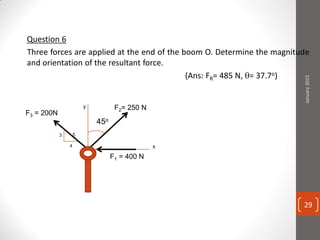
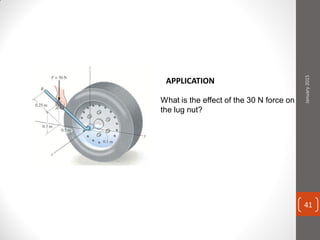
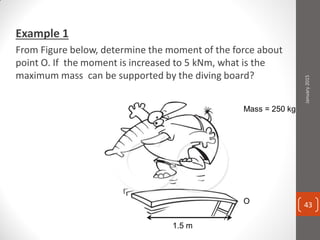
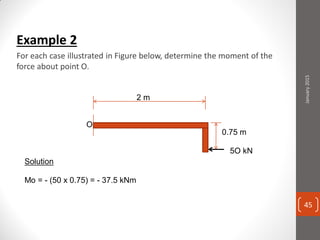
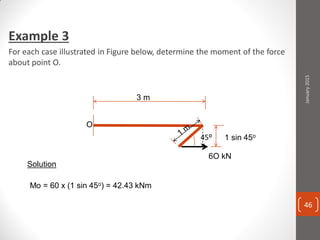
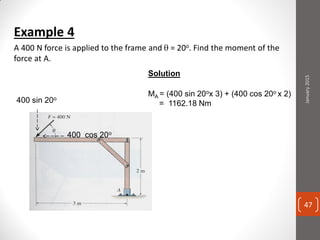
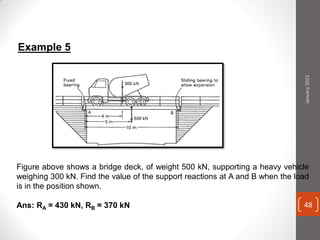
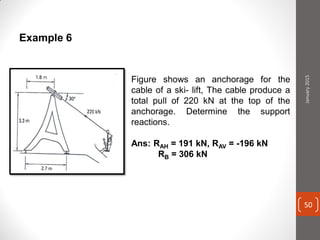
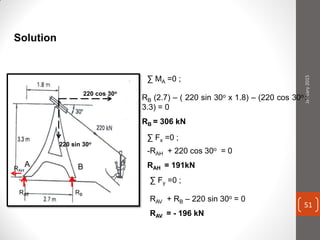
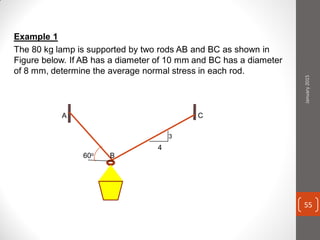
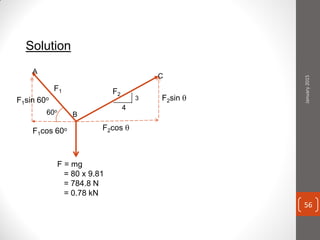
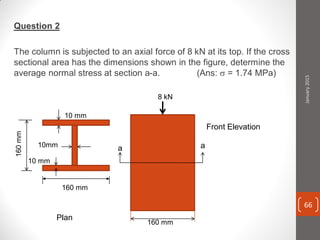
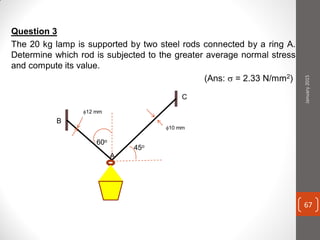
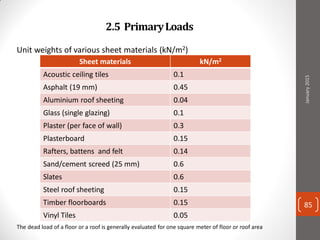
The cable produces a total pull of 220 kN at the top of the anchorage. Let's break this problem down step-by-step: 1) Resolve the 220 kN force into horizontal (RAH) and vertical (RAV) components: RAH = 220 cos 30° = 191 kN RAV = 220 sin 30° = -196 kN (note the negative sign indicates downward direction) 2) The horizontal and vertical equilibrium equations are satisfied: ΣH = RAH - 0 = 0 ΣV = RAV - (-196) = 0 Therefore, the support reactions are: RAH = 191 kN RAV = -196 kN

Embed presentation

Download as PDF, PPTX
Chapter 2 Basic Structure Concepts January2015 1
2.0 : BASIC STRUCTURE CONCEPT 2.1 Forces 2.2 Equilibrium and Reactions 2.3 Moments 2.4 Stress and Strain 2.5 Elastic and plastic range 2.6 Primary Loads & Secondary Loads January2015 2
2.1 Forces A force is that which tends to exert motion, tension or compression on an object. The loads acting on a structure have mass which is usually measured in kilograms(kg). The basic unit of force is the newton (N). The force exerted on a structure by a static load is dependent upon both its mass and the force of gravity. The force exerted by a body as a result of gravity can be described as its weight. F =W= m x g  Therefore, the force exerted by a mass of 1 kg is: F = m x g = 1 x 9.81 =9.81 N @ 0.00981 kN  1 kN = 1000 N January2015 3
2.1 Forces Scalars and Vectors Scalars Vectors Examples: mass, volume force, velocity Characteristics: It has a magnitude It has a magnitude (positive or negative) and direction Addition rule: Simple arithmetic Parallelogram law Special Notation: None Bold font, a line, an arrow or a “carrot” January2015 4
2.1 Forces Application of Vector Addition There are four concurrent cable forces acting on the bracket. How do you determine the resultant force acting on the bracket ? January2015 5
2.1 Forces Vector Operations Scalar Multiplication and Division January2015 6
2.1 Forces Vector Addition Using Either the Parallelogram or Triangle Parallelogram Law: Triangle method (always ‘tip to tail’): How do you subtract a vector? How can you add more than two concurrent vectors graphically ? January2015 7
2.1 Forces Resolution of a vector “Resolution” of a vector is breaking up a vector into components. It is kind of like using the parallelogram law in reverse. January2015 8
2.1 Forces  Each component of the vector is shown as a magnitude and a direction. Cartesian Vector Notation We ‘ resolve’ vectors into components using the x and y axes system  The directions are based on the x and y axes. We use the “unit vectors” i and j to designate the x and y axes. January2015 9
2.1 Forces For example, F = Fx i + Fy j or F' = F'x i + F'y j The x and y axes are always perpendicular to each other. Together, they can be directed at any inclination. January2015 10
2.1 Forces Addition of Several Vectors Step 1 is to resolve each force into its components  Step 2 is to add all the x components together and add all the y components together. These two totals become the resultant vector. Step 3 is to find the magnitude and angle of the resultant vector. January2015 11
2.1 Forces January2015 12
2.1 Forces January2015 13
2.1 Forces Example 1 The screw eye in Figure below is subjected to forces F1 and F2. Determine the magnitude and direction (measured from x- positive axis) of the resultant force. F2= 150 N F1= 100 N10o 15o January2015 14
2.1 Forces Solution 10o 15o 15o + 90o + 10o = 115o R =√(1002 +1502 – (2x 100 x 150 x cos 115 ) = 212.55 N  Sin /150 = sin 115/212.55 Sin  = (sin 115/212.55) x 150  = 39.76o Direction = 15o + 39.76o =54.76o January2015 15
2.1 Forces Example 2 Determine the magnitude of the resultant force and its direction, measured clockwise from the positive x-axis Solution a) Resolve the forces in their x-y components. b) Add the respective components to get the resultant vector. c) Find magnitude and angle from the resultant components. January2015 16
2.1 Forces F1 = { 15 sin 40° i + 15 cos 40° j } kN = { 9.642 i + 11.49 j } kN F2 = { -(12/13)26 i + (5/13)26 j } kN = { -24 i + 10 j } kN F3 = { 36 cos 30° i – 36 sin 30° j } kN = { 31.18 i – 18 j } kN January2015 17
2.1 Forces Summing up all the i and j components respectively, we get, FR = { (9.642 – 24 + 31.18) i + (11.49 + 10 – 18) j } kN = { 16.82 i + 3.49 j } kN FR = ((16.82)2 + (3.49)2)1/2 = 17.2 kN  = tan-1(3.49/16.82) = 11.7° January2015 18
2.1 Forces Example 3 Determine the magnitude of the resultant force and its direction, measured counterclockwise from the positive x axis Solution a) Resolve the forces in their x-y components. b) Add the respective components to get the resultant vector. c) Find magnitude and angle from the resultant components. January2015 19
2.1 Forces F1 = { (4/5) 850 i - (3/5) 850 j } N = { 680 i - 510 j } N F2 = { -625 sin(30°) i - 625 cos(30°) j } N = { -312.5 i - 541.3 j } N F3 = { -750 sin(45°) i + 750 cos(45°) j } N { -530.3 i + 530.3 j } N January2015 20
2.1 Forces Summing up all the i and j components respectively, we get, FR = { (680 – 312.5 – 530.3) i + (-510 – 541.3 + 530.3) j }N = { - 162.8 i - 521 j } N FR = ((162.8)2 + (521)2) ½ = 546 N = tan–1(521/162.8) = 72.64° or From Positive x axis  = 180 + 72.64 = 253 ° January2015 21
TUTORIAL 1 (FORCES) Question 1 Two forces are applied to an eye bolt fastened to a beam. Determine the magnitude and direction of their resultant. 6 kN 4.5 kN 25o 50o January2015 22
Question 2 Two forces P and Q are applied as shown at point A of a hook support. Knowing that P = 60 kN and Q = 100 kN. Determine the magnitude and direction of their resultant. (Ans: R = 150 kN, 76o towards x axis positive) P Q 15o 30o January2015 24
Question 3 The cables AB and AD help support pole AC. Knowing that the tension is 500 N in AB and 160 N in AD. Determine the magnitude and direction of the resultant of the forces exerted by cables at A. (Ans: R = 575 N, 113o towards x axis positive) A B C D 2 m 1.5 m 2.5 m January2015 25
Question 4 Determine the resultant and direction from x-axis positive of the five forces shown in Figure below by the graphical method. (Ans: R = 32.5 kN, = 124o) y x 8 kN 9 kN 4 kN 60o 25 kN 3 kN 15o 30o 20o January2015 26
Question 5 Determine the magnitude and direction measured counterclockwise from the positive x axis of the resultant force of the three acting on the ring A. Take F1 = 500 N and  = 20o (Ans: R = 1.03 kN, = 87.9o) y x 600 N F1 400 N 30o 3 4 5 January2015 27
Question 6 Three forces are applied at the end of the boom O. Determine the magnitude and orientation of the resultant force. (Ans: FR= 485 N, = 37.7o) y x F3 = 200N F2= 250 N F1 = 400 N 45o 3 4 5 January2015 29
• Question 7 • Two cables are attached to the frame shown in Figure below. Using trigonometry, determine : (a) the required magnitude of the force P if the resultant R of the two forces applied at A is to be vertical. (b) the corresponding magnitude of R. (Ans: 489 N, 738 N) A A 25o 35o 360 N P January2015 30
2.2 Equilibriumand Reactions Any structure subjected to loads must be provided with supports to prevent it from moving. The forces generated on the structure by these supports are called reactions. If the structure is in equilibrium (i.e. not moving) then the net forces from the loads and reactions must be zero in all directions. Fx = 0 Fy = 0  M = 0 January2015 31
January2015 32
Example 1 Determine the magnitudes of F1 and F2 so that particle P is in equilibrium. (Ans: F1 = 435 N, F2 = 171 N) P F1 F2 400 N 3 4 5 30o 60o January2015 33
Solution The two unknown magnitudes F1 and F2 can be obtained from the two scalar equations of equilibrium, ∑Fx=0 and ∑Fy = 0. To apply these equations, the x, y axes are established on the free body diagram and forces must be resolved into its x and y components. P F1 F2 400 N 3 4 5 30o 60o 400 cos 30o 400 sin 30o F2 cos 60o F2 sin 60o F1 (4/5) F1 (3/5) January2015 34
Solution ∑ Fx =0 ; -400 sin 30o + F1(4/5) –F2sin 60o=0 ∑ Fy =0; 400 cos 30o -F1(3/5) –F2cos 60o=0 (1) (2) Simplify : 0.8 F1 – 0.866 F2 = 200 (3) -0.6 F1 – 0.5 F2 = -346.61 (4) Solving Eqs. (3) & (4) by simultaneous equations to determine F1 & F2. Ans : F1 = 435.08 N F2 = 170.97 N January2015 35
Applicationof equilibriumconceptsin truss  A truss is a structure composed of slender members joined together at their end points.  The members commonly used in construction consist of wooden struts or metal bars  The joint connections are usually formed by bolting or welding the ends of the members to a common plate, called a gusset plate, as shown in Fig below. January2015 36
January2015 37
38 Timber Roof Trusses Steel Bridge Trusses January2015
Example • Determine the force in each member of the Pratt bridge truss shown. State whether each member is in tension or compression. 6 kN 6 kN 6 kN 4 m 3 m 3 m 3 m 3 m A B C D E F G H January2015 39
2.3 Moments APPLICATION What is the net effect of the two forces on the wheel? January2015 40
APPLICATION What is the effect of the 30 N force on the lug nut? January2015 41
 The moment of a force about a point or axis provides a measure of the tendency of the force to cause a body to rotate about the point or axis.  This tendency for rotation caused by force is sometimes called a torque, but most often it is called the moment of a force or simply the moment  The magnitude of a moment about a point is the value of the force multiplied by the perpendicular distance from the line of action of the force to the point  M= T = F x d  The unit is Nm or kNm The typical sign convention for moment is that counter-clockwise is considered positive. January2015 42
Example 1 From Figure below, determine the moment of the force about point O. If the moment is increased to 5 kNm, what is the maximum mass can be supported by the diving board? 1.5 m Mass = 250 kg January2015 43
Solution F = mg = 250 (9.81)= 2452.5 N = 2.45 kN 1.5 m Mo = ( 2.45 x 1.5) = 3.68 kNm If Mo = 5 kNm, then new load is Mo = F x d 5 = F x 1.5 F = 3.33 kN = 3333.33 N F = m x g 3333.33 = m x 9.81 m = 339.79 kg F January2015 44
Example 2 For each case illustrated in Figure below, determine the moment of the force about point O. 5O kN 2 m 0.75 m Solution Mo = - (50 x 0.75) = - 37.5 kNm January2015 45
Example 3 For each case illustrated in Figure below, determine the moment of the force about point O. 6O kN 3 m 45o Solution 1 sin 45o Mo = 60 x (1 sin 45o) = 42.43 kNm January2015 46
Example 4 A 400 N force is applied to the frame and  = 20o. Find the moment of the force at A. Solution 400 sin 20o 400 cos 20o MA = (400 sin 20ox 3) + (400 cos 20o x 2) = 1162.18 Nm January2015 47
Figure above shows a bridge deck, of weight 500 kN, supporting a heavy vehicle weighing 300 kN. Find the value of the support reactions at A and B when the load is in the position shown. Ans: RA = 430 kN, RB = 370 kN Example 5 January2015 48
Solution 500 kN 5 m 300 kN A B 4 m ∑ MA =0 ; ∑ Fy =0 ; RB (10) – ( 300 x 4) – (500 x 5) = 0 RB = 370 kN RA + RB – 300 – 500 = 0 RA = 430 kN January2015 49
Example 6 Figure shows an anchorage for the cable of a ski- lift, The cable produce a total pull of 220 kN at the top of the anchorage. Determine the support reactions. Ans: RAH = 191 kN, RAV = -196 kN RB = 306 kN January2015 50
Solution A B 220 cos 30o 220 sin 30o RBRAV RAH ∑ MA =0 ; RB (2.7) – ( 220 sin 30o x 1.8) – (220 cos 30o x 3.3) = 0 RB = 306 kN ∑ Fx =0 ; -RAH + 220 cos 30o = 0 RAH = 191kN RAV + RB – 220 sin 30o = 0 RAV = - 196 kN ∑ Fy =0 ; January2015 51
2.4 Stress and Strain Stress Concept of stress  To obtain distribution of force acting over a sectioned area  Assumptions of material: 1. It is continuous (uniform distribution of matter) 2. It is cohesive (all portions are connected together) Normal stress  Intensity of force, or force per unit area, acting normal to ΔA  Symbol used for normal stress, is σ (sigma) σz = lim ΔA →0 ΔFz ΔA January2015 52
 Tensile stress: normal force “pulls” or “stretches” the area element ΔA  Compressive stress: normal force “pushes” or “compresses” area element ΔA  Shear stress  Intensity of force, or force per unit area, acting tangent to ΔA  Symbol used for normal stress is τ (tau) τzx = lim ΔA →0 ΔFx ΔA τzy = lim ΔA →0 ΔFy ΔA Units (SI system) Newtons per square meter (N/m2) or a pascal (1 Pa = 1 N/m2) kPa = 103 N/m2 (kilo-pascal) MPa = 106 N/m2 (mega-pascal) GPa = 109 N/m2 (giga-pascal) January2015 53
Shear in Nature January2015 54
Example 1 The 80 kg lamp is supported by two rods AB and BC as shown in Figure below. If AB has a diameter of 10 mm and BC has a diameter of 8 mm, determine the average normal stress in each rod. A B C 60o 3 4 January2015 55
A B C 60o 3 4 F = mg = 80 x 9.81 = 784.8 N = 0.78 kN F1 F2 F1cos 60o F1sin 60o F2cos  F2sin  Solution January2015 56
Solution ∑ Fx =0 ; – F1cos 60o + F2(4/5) =0 ∑ Fy =0; F1sin 60o+ F2(3/5) – 0.78 =0 (1) (2) Simplify : - 0.5 F1 + 0.8 F2 = 0 (3) 0.866 F1 + 0.6 F2 = 0.78 (4) Solving Eqs. (3) & (4) by simultaneous equations to determine F1 & F2. 0.6 x Eqs (3) - 0.3 F1 + 0.48 F2 = 0 0.8 x Eqs (4) 0.69 F1 + 0.48 F2 = 0.624 - 0.99 F1 = - 0.624 F1 = 0.63 kN Subs F1 into Eqs (3) - - 0.5 F1 + 0.8 F2 = 0 - 0.5 x 0.63 + 0.8 F2 = 0 F2 = 0.315/0.8 = 0.39 kN January2015 57
Solution 1 = F1 / A1 = 0.63 /( x 0.0052) = 8021.41 kN/m2 2 = F2 / A2 = 0.39/( x 0.0042) = 7758.8 kN/m2 January2015 58
Shear Stress  Shear stress is the stress component that act in the plane of the sectioned area.  Consider a force F acting to the bar  For rigid supports, and F is large enough, bar will deform and fail along the planes identified by AB and CD  Free-body diagram indicates that shear force, V = F/2 be applied at both sections to ensure equilibrium January2015 59
Average shear stress over each section is: P Aavg = avg = average shear stress at section, assumed to be same at each pt on the section V = internal resultant shear force at section determined from equations of equilibrium A = area of section January2015 60
Example 1 The bar shown in Figure below has a square cross section for which the depth and thickness are 40 mm. If an axial force of 800 N is applied along the centroidal axis of the bar’s cross-sectional area, determine average normal stress and average shear stress acting on the material along section planes a-a. January2015 61
Internal loading Based on free-body diagram, Resultant loading of axial force, P = 800 N Average normal stress = P/A = 800/(0.04)(0.04) = 500 kPa Average shear stress No shear stress exists on the section, since the shear force at the section is zero. January2015 62
Example 2 Three plates are held together by two cyclindrical rivets. If a direct pull of 5 kN is applied between one plate and the other two, estimate the diameter of the rivets. The shear stress in the rivets is not to exceed 40 N/mm2. 5 kN January2015 63
Solution • 4 sliding areas (Double shear) P A = 40 = 5000 4(2/4)  = 6.3 mm January2015 64
Question 1 A 50 kN axial load is applied to a short wooden post which is supported by a square concrete footing resting on distributed soil. Determine (a) The maximum bearing stress on the concrete footing (b) The size of the footing for which the average bearing stress on the soil is 150 kPa. (Ans: B = 4MPa, b= 577 mm) Plan 125 mm 100 mm b b 50 kN January2015 65 TUTORIAL 2 (STRESS
Question 2 The column is subjected to an axial force of 8 kN at its top. If the cross sectional area has the dimensions shown in the figure, determine the average normal stress at section a-a. (Ans:  = 1.74 MPa) Plan Front Elevation 160 mm 160 mm a a 10 mm 10mm 10 mm 8 kN 160mm January2015 66
Question 3 The 20 kg lamp is supported by two steel rods connected by a ring A. Determine which rod is subjected to the greater average normal stress and compute its value. (Ans:  = 2.33 N/mm2) B A C 60o 45o 12 mm 10 mm January2015 67
Question 4 A square hole having 12 mm sides is to be punched out of a metal plate 1.6 mm thick. The shear stress required to cause fracture is 350 N/mm2. What force must be applied to punch die? What would be the compressive stress in the punch? (Ans: 26.88 kN, 0.19 kN/mm2) January2015 68
ALLOWABLE STRESS  When designing a structural member or mechanical element, the stress in it must be restricted to safe level  Choose an allowable load that is less than the load the member can fully support  One method used is the factor of safety (F.S.) F.S. = Ffail Fallow  If load applied is linearly related to stress developed within member, then F.S. can also be expressed as: F.S. = σfail σallow F.S. = fail allow  In all the equations, F.S. is chosen to be greater than 1, to avoid potential for failure  Specific values will depend on types of material used and its intended purpose January2015 69
Strain  Loads cause bodies to deform, thus points in the body will undergo displacements or changes in position  Normal strain () is a measure of elongation or contraction of small line segment in the body Normal Strain () = Change in length = L Original length L  Has no unit  Shear strain () is a measure of the change in angle that occurs between two small line segments that are originally perpendicular to each other. Shear Strain () = x L L x January2015 70
Conventional stress-strain diagram  Figure shows the characteristic stress-strain diagram for steel, a commonly used material for structural members and mechanical elements January2015 71
Elastic behavior.  A straight line  Stress is proportional to strain, i.e., linearly elastic  Upper stress limit, or proportional limit; σpl  If load is removed upon reaching elastic limit, specimen will return to its original shape January2015 72
Yielding.  Material deforms permanently; yielding; plastic deformation  Yield stress, σY  Once yield point reached, specimen continues to elongate (strain) without any increase in load  Note figure not drawn to scale, otherwise induced strains is 10-40 times larger than in elastic limit  Material is referred to as being perfectly plastic January2015 73
Strain hardening.  Ultimate stress, σu  While specimen is elongating, its x- sectional area will decrease  Decrease in area is fairly uniform over entire gauge length January2015 74
Necking.  At ultimate stress, x-sectional area begins to decrease in a localized region  As a result, a constriction or “neck” tends to form in this region as specimen elongates further  Specimen finally breaks at fracture stress, σf January2015 75
Hooke’s Law When a material is worked within its elastic limit, the extension is proportional to the force. Strain  Stress Stress = Constant (E) Strain This constant is known as the modulus of elasticity or Young’s Modulus January2015 76
Example 1 A tie-bar in a steel structure is of rectangular section 30 mm x 50 mm. The extension measured in a 250 mm length of the tie bar when load is applied to the structure is 0.1 mm. Find :- i) The tensile stress in the bar ii) The tensile force iii) The factor of safety used Take E = 205 kN/mm2 and Ultimate stress = 460 N/mm2 January2015 77
Solution i) The tensile stress in the bar E = stress/strain Strain (ε) = ∆L/L = 0.1/250 = 4 x 10-4 E = stress/strain 205 = / 4 x 10-4  = 205 x 4 x 10-4 = 0.082 kN/mm2 = 82 N/mm2 ii) The tensile force  = F/A 82 = F/(30 x 50) F = 82 x (30 x 50) = 123,000 = 123 kN iiii) The factor of safety used F.S. = Ultimate stress/ Tensile stress = 460 /82 = 5.6 January2015 78
Example 2 The ultimate stress for a steel is 450 N/mm2. What is the maximum load which a rod 50 mm diameter can carry with a factor of safety of 5? If the rod is 1.5 m long, determine the extension under this loading.( E = 200 kN/mm2.) Solution The factor of safety F.S. = Ultimate stress/ Tensile stress 5 = 450 / tensile stress Tensile stress = 450/5 = 90 N/mm2  = F/A 90 = F/(π r2) F = 90 x (π x 252) = 176,714.59 N = 176.71 kN January2015 79
Solution The tensile stress in the bar E = stress/strain 200 x 103 = 90/ ε ε = 90/ 200 x 103 = 4.5 x 10-4 Strain (ε) = ∆L/L 4.5 x 10-4 = ∆L/1500 ∆L = 0.675 mm January2015 80
Exercise 1 A flat steel tie-bar 4.5 m long, is found to be 2.4mm short. It is sprung into place by means of drafts driven into holes in the end of the bar. Determine: (a) the stress in the bar (b) the factor of safety if the material of the tie-bar has an ultimate stress of 450 N/mm2. Take E for the material as 205 kN/mm2. ( Ans: 109.3 N/mm2, 4.117) January2015 81 TUTORIAL 3 (STRESS, STRAIN & FACTOR OF SAFETY)
Exercise 2 A metal tube of outside diameter 75 mm and length 1.65 m is to carry a compressive load of 60 kN. If the allowable axial stress is 75 N/mm2 , calculate the inside diameter of the tube. If E of the material is 90 kN/mm2., by how much will the tube shorten under this load? Ans: 67.87 mm, 1.375 mm) January2015 82
2.5 PrimaryLoads & Secondary Loads  DEADLOADS Dead Loads are those loads which are considered to act permanently; they are "dead," stationary, and unable to be removed. The self-weight of the structural members normally provides the largest portion of the dead load of a building. This will clearly vary with the actual materials chosen. Permanent non-structural elements such as roofing, concrete, flooring, pipes, ducts, interior partition walls, Environmental Control Systems machinery, elevator machinery and all other construction systems within a building must also be included in the calculation of the total dead load. These loads are represented by the red arrow in the illustration. Primary Loads are divided into three broad categories according to the way in which they act upon the structure or structural element. These are DEAD LOADS, LIVE LOADS(IMPOSED LOADS) and WIND LOADS January2015 83
2.5PrimaryLoads Unit weights of various building materials (kN/m3) Materials Unit Weight Aluminium 24 Bricks 22* Concrete 24 Concrete blocks (lightweight) 12* Concrete blocks (dense) 22* Glass fibre composite 18 Steel 70 Timber 6* * Subject to considerable variation January2015 84
2.5 PrimaryLoads Unit weights of various sheet materials (kN/m2) The dead load of a floor or a roof is generally evaluated for one square meter of floor or roof area Sheet materials kN/m2 Acoustic ceiling tiles 0.1 Asphalt (19 mm) 0.45 Aluminium roof sheeting 0.04 Glass (single glazing) 0.1 Plaster (per face of wall) 0.3 Plasterboard 0.15 Rafters, battens and felt 0.14 Sand/cement screed (25 mm) 0.6 Slates 0.6 Steel roof sheeting 0.15 Timber floorboards 0.15 Vinyl Tiles 0.05 January2015 85
• LIVE LOADS Live Loads are not permanent and can change in magnitude. They include items found within a building such as furniture, pianos, safes, people, books, cars, computers, machinery, or stored materials, as well as environmental effects such as loads due to the sun, earth or weather. • WIND LOADS Wind and earthquakes loads are put into the special category of lateral live loads due to the severity of their action upon a building and their potential to cause failure. January2015 86
Secondary loads Structures can be subjected to secondary loads from temperature changes, shrinkage of members and settlement of supports. January2015 87
Example 1 Figure shows a precast concrete Beam which is 10.5 m long. a) Calculate the weight of the beam per unit length in kN/m b) Calculate the total weight of the beam January2015 88
Solution a) Cross sectional area of the beam = (0.6 x 0.25) – (0.4 x 0.15) = 0.09 m2 Unit weight of concrete = 24 kN/m3 Weight per unit length = 0.09 x 24 = 2.16 kN/m b) Total weight of the beam = 2.16 x 10.5 = 22.68 kN January2015 89
Example 2 The floor in a multi-storey office. Building consists of the following: • Vinyl tiles • 40 mm sand/cement screed • 125 mm reinforced concrete slab • Acoustic tile suspended ceiling Determine the dead load in kN/m2 January2015 90
Solution From the table given • Vinyl tiles = 0.05 • 40 mm sand/cement screed = 0.6 x (40/25) = 0.96 • 125 mm reinforced concrete = 0.125 x 24 = 3.00 slab • Acoustic tile suspended ceiling = 0.10 The dead load = 4.11 kN/m2 January2015 91
Exercise 1 Figure shows the outer wall of a multi-storey building which is supported on a beam at each floor level. The wall consist of a 1.2 m height of cavity wall supporting 1.3 m high double glazing. The cavity wall construction is 102.5 mm of brickwork, a 75 mm cavity and 100 mm of plastered lightweight concrete blockwork. Determine the dead load on one beam in kN/m of beam. (Ans: 4.77 kN/m) January2015 92 TUTORIAL 4 (LOADS)

More Related Content

PPTX
PILE foundation (1).pptx
byNIKHILBANDWAL1
 
PDF
9789810682460 sm 06
byaryaanuj1
 
PPT
Resultant of forces
byHUSSAIN SHAIK
 
PDF
01 01 chapgere[1]
byCharles Jumbo
 
PDF
Liquids in relative equilibrium
byphysics101
 
PPTX
Centroid
byserinsara
 
PDF
psad 1.pdf
byRobin Arthur Flores
 
PPTX
Kinetics of a Particle : Force and Acceleration
byAbduljalil AlAbidi
 
PILE foundation (1).pptx
byNIKHILBANDWAL1
 
9789810682460 sm 06
byaryaanuj1
 
Resultant of forces
byHUSSAIN SHAIK
 
01 01 chapgere[1]
byCharles Jumbo
 
Liquids in relative equilibrium
byphysics101
 
Centroid
byserinsara
 
psad 1.pdf
byRobin Arthur Flores
 
Kinetics of a Particle : Force and Acceleration
byAbduljalil AlAbidi
 

What's hot

PPTX
Truss for indeterminacy Check
bymahafuzshawon
 
PPTX
Coplanar Non-concurrent Forces
byMahesh Bajariya
 
PPTX
COPLANNER & NON-CONCURRENT FORCES
byAkash Patel
 
PPS
Statics free body diagram
byGourav Kapoor
 
PDF
STRUCTURAL ANALYSIS NINTH EDITION R. C. HIBBELER
byBahzad5
 
PDF
Structural Analysis (Solutions) Chapter 9 by Wajahat
byWajahat Ullah
 
PDF
Mecanica
byGlobal
 
PDF
Connection design
bydattavan
 
PPTX
Structural Mechanics - lec 1
byCivil Zone
 
PPT
Bab2
byshaifulawie77
 
PDF
Influence lines (structural analysis theories)
byMadujith Sagara
 
PPTX
Slope Deflection Method
byMahdi Damghani
 
PPTX
III - resultant of non-concurrent forces
bydjpprkut
 
PDF
Stiffness matrix method for beam , examples ce525
byKAMARAN SHEKHA
 
PPTX
Problems on simply supported beams
bysushma chinta
 
PPTX
Direct integration method
byMahdi Damghani
 
PDF
structural analysis CE engg. solved ex.
byIMALONE1
 
PDF
trusses
byFazirah Abdul Ghafar
 
PDF
Continuity in RC beams and frames-AFM (Complete).pdf
byaslhal
 
PDF
Mechanics of Materials 8th Edition R.C. Hibbeler
byBahzad5
 
Truss for indeterminacy Check
bymahafuzshawon
 
Coplanar Non-concurrent Forces
byMahesh Bajariya
 
COPLANNER & NON-CONCURRENT FORCES
byAkash Patel
 
Statics free body diagram
byGourav Kapoor
 
STRUCTURAL ANALYSIS NINTH EDITION R. C. HIBBELER
byBahzad5
 
Structural Analysis (Solutions) Chapter 9 by Wajahat
byWajahat Ullah
 
Mecanica
byGlobal
 
Connection design
bydattavan
 
Structural Mechanics - lec 1
byCivil Zone
 
Bab2
byshaifulawie77
 
Influence lines (structural analysis theories)
byMadujith Sagara
 
Slope Deflection Method
byMahdi Damghani
 
III - resultant of non-concurrent forces
bydjpprkut
 
Stiffness matrix method for beam , examples ce525
byKAMARAN SHEKHA
 
Problems on simply supported beams
bysushma chinta
 
Direct integration method
byMahdi Damghani
 
structural analysis CE engg. solved ex.
byIMALONE1
 
trusses
byFazirah Abdul Ghafar
 
Continuity in RC beams and frames-AFM (Complete).pdf
byaslhal
 
Mechanics of Materials 8th Edition R.C. Hibbeler
byBahzad5
 

Viewers also liked

PDF
Types of radioactive decay
byDavid Graff
 
PPTX
Chapter 22.2 : Radioactive Decay
byChris Foltz
 
PPTX
Isotop, isobar dan isoton
byABINUL HAKIM
 
PPTX
Radioactivity + isotopes lect.1,2,
bykamal2200
 
PPT
Isotopes And Radioactivity 09
byPaula Mills
 
PPTX
isotop, isobar, isoton
byberlianablue
 
PPTX
ISOTOP, ISOTON DAN ISOBAR
byHome
 
PPT
Atomic theory timeline
byramatboy
 
PDF
Introduction to Electron Correlation
byAlbert DeFusco
 
PPTX
Nuclear Materials
byAnuroop Ashok
 
PPTX
Isotopes, isotones, and isobars
byEvina Nathalia
 
PPTX
Isotope isotone isobar
byFendi Ard
 
PDF
Option C Nuclear Physics, Radioactive decay and half life
byLawrence kok
 
KEY
Models of the Atom
byOhMiss
 
PPT
RADIOACTIVE DECAY AND HALF-LIFE CONCEPTS
bySciencetutors E-learning Media
 
PPT
Nuclear Power Taja
byRosalmara
 
PPTX
Radioactivity.ppt
byAshaduzzaman Kanon
 
PPTX
DIFFERENT ATOMIC MODELS
byShahn Tee
 
PPT
Atomic Theory power point cscope
byJenny Dixon
 
PPT
Nucleus Ppt
byiyss0104
 
Types of radioactive decay
byDavid Graff
 
Chapter 22.2 : Radioactive Decay
byChris Foltz
 
Isotop, isobar dan isoton
byABINUL HAKIM
 
Radioactivity + isotopes lect.1,2,
bykamal2200
 
Isotopes And Radioactivity 09
byPaula Mills
 
isotop, isobar, isoton
byberlianablue
 
ISOTOP, ISOTON DAN ISOBAR
byHome
 
Atomic theory timeline
byramatboy
 
Introduction to Electron Correlation
byAlbert DeFusco
 
Nuclear Materials
byAnuroop Ashok
 
Isotopes, isotones, and isobars
byEvina Nathalia
 
Isotope isotone isobar
byFendi Ard
 
Option C Nuclear Physics, Radioactive decay and half life
byLawrence kok
 
Models of the Atom
byOhMiss
 
RADIOACTIVE DECAY AND HALF-LIFE CONCEPTS
bySciencetutors E-learning Media
 
Nuclear Power Taja
byRosalmara
 
Radioactivity.ppt
byAshaduzzaman Kanon
 
DIFFERENT ATOMIC MODELS
byShahn Tee
 
Atomic Theory power point cscope
byJenny Dixon
 
Nucleus Ppt
byiyss0104
 

Similar to Chapter 2 basic structure concepts

PPTX
ME 121 - Lecture 5 and 6 - Force Systems - Chapter 2 - Engineering Statics.pptx
byHashirKhan62
 
PPT
EM Forces in Space.ppt
bydharma raja`
 
PPT
chapter1and2.ppt
byRanaUmair74
 
PPSX
Basics and statics of particles unit i - GE6253 PPT
byTHANGA KASI RAJAN S
 
PPTX
Concurrent Force System SPP.pptx
byDharmsinh Desai of University
 
PPT
Statics
byRamasubbu .P
 
PPTX
General system of forces unit 4 bce & engg mechanics
byParimal Jha
 
PPTX
Ctm 154[1]
by0242694327
 
PPTX
Chapter 2 Force System NEW 2Dimensional force system.pptx
byshelemaabate2
 
PPTX
SAFASFASDFSDFSDFSDGDSGSGFDGFDHGHFDGFDGFG
byssuser3574f6
 
PDF
Mechanics full notes
byshilumbuhelfric
 
PPT
chap2_force_systems - Copy.ppt
byteseraaddis1
 
PDF
Chapter-2.pdffsdfsdfsdfsdfsdfsdfsdfsdfsdfsd
bybarbaroscngl
 
PDF
16201806 bahan-ajar-ptm117-mekanika-teknik
byDedy Wonkso
 
PPTX
Chapter 2: Two dimenstional force systems: DBU-MESA
byYitagesu Ethiopia
 
PPTX
Diploma i em u ii forces and its effects
byRai University
 
PDF
Notes on Applied Mechanics of Happiness and success in your long life me kuch...
byfaishalraza888
 
PDF
Coplanar forces res & comp of forces - for merge
byEkeeda
 
PDF
coplanar forces res comp of forces - for merge
byEkeeda
 
PDF
Engineering Mechanics Pdf
byEkeeda
 
ME 121 - Lecture 5 and 6 - Force Systems - Chapter 2 - Engineering Statics.pptx
byHashirKhan62
 
EM Forces in Space.ppt
bydharma raja`
 
chapter1and2.ppt
byRanaUmair74
 
Basics and statics of particles unit i - GE6253 PPT
byTHANGA KASI RAJAN S
 
Concurrent Force System SPP.pptx
byDharmsinh Desai of University
 
Statics
byRamasubbu .P
 
General system of forces unit 4 bce & engg mechanics
byParimal Jha
 
Ctm 154[1]
by0242694327
 
Chapter 2 Force System NEW 2Dimensional force system.pptx
byshelemaabate2
 
SAFASFASDFSDFSDFSDGDSGSGFDGFDHGHFDGFDGFG
byssuser3574f6
 
Mechanics full notes
byshilumbuhelfric
 
chap2_force_systems - Copy.ppt
byteseraaddis1
 
Chapter-2.pdffsdfsdfsdfsdfsdfsdfsdfsdfsdfsd
bybarbaroscngl
 
16201806 bahan-ajar-ptm117-mekanika-teknik
byDedy Wonkso
 
Chapter 2: Two dimenstional force systems: DBU-MESA
byYitagesu Ethiopia
 
Diploma i em u ii forces and its effects
byRai University
 
Notes on Applied Mechanics of Happiness and success in your long life me kuch...
byfaishalraza888
 
Coplanar forces res & comp of forces - for merge
byEkeeda
 
coplanar forces res comp of forces - for merge
byEkeeda
 
Engineering Mechanics Pdf
byEkeeda
 

More from Simon Foo

PDF
Lecture12 new movement
bySimon Foo
 
PDF
Lecture11 late modernism heavy masonry ; brutalism
bySimon Foo
 
PDF
Lecture10 the rise of suburbia ; the modern house
bySimon Foo
 
PDF
Lecture9 totalitarian architecture
bySimon Foo
 
PDF
Lecture8 international style
bySimon Foo
 
PDF
Lecture6 abstraction of forms and line
bySimon Foo
 
PDF
Lecture5 early modern
bySimon Foo
 
PDF
Lecture4 art nouvou
bySimon Foo
 
PDF
Lecture2 arts & crafts movement
bySimon Foo
 
PDF
Lecture3 victorian electisism
bySimon Foo
 
PDF
Chapter 6 column
bySimon Foo
 
PDF
Chapter 5 beams design
bySimon Foo
 
PDF
Chapter 3 beam
bySimon Foo
 
PDF
Chapter 1 introduction to structure
bySimon Foo
 
Lecture12 new movement
bySimon Foo
 
Lecture11 late modernism heavy masonry ; brutalism
bySimon Foo
 
Lecture10 the rise of suburbia ; the modern house
bySimon Foo
 
Lecture9 totalitarian architecture
bySimon Foo
 
Lecture8 international style
bySimon Foo
 
Lecture6 abstraction of forms and line
bySimon Foo
 
Lecture5 early modern
bySimon Foo
 
Lecture4 art nouvou
bySimon Foo
 
Lecture2 arts & crafts movement
bySimon Foo
 
Lecture3 victorian electisism
bySimon Foo
 
Chapter 6 column
bySimon Foo
 
Chapter 5 beams design
bySimon Foo
 
Chapter 3 beam
bySimon Foo
 
Chapter 1 introduction to structure
bySimon Foo
 

Recently uploaded

PPTX
lecture 1 Machine tools the introduction
bypushkarkamble2
 
PDF
Mahabir - Structural Steel Brochure - 2025
byMahabirIndustries1
 
PDF
Julian Kalac -GEN AI inventive solution Automated SOC Report Processing .pdf
byJulian Kalac P.Eng
 
PPTX
Energy system modelling to support national energy and climate policy making ...
byIEA-ETSAP
 
DOCX
Hallucination Reduction In Generative Artificial Intelligence (1).docx
by21nitinsinha
 
PDF
Earths-Structure-and-Composition_20260127_110958_0000.pdf
byabdurasabarfaki
 
PDF
Software Engineering :Software Engineering Practice
byGunjalSanjay
 
PDF
Software Engineering : Process Model
byGunjalSanjay
 
PDF
LS029B3SX06A 2.9 Inch TFT LCD 2K Resolution 2160X2160 For AR VR
bySyluxdisplay
 
PDF
PASSIVE AND ACTIVE REINFORCEMENT LEARNING
byAnushaSanjay
 
PPTX
Lecture 2 Machine tool - time calculations
bypushkarkamble2
 
PDF
Disaster Management Notes for B.Tech. CSE
byhemish04082005
 
PDF
BCS402 MICROCONTROLLERS MODULE 1
byAbhijith L Kotian
 
PDF
Reality Check Deploying Computer Vision and LLMs at the Edge
byICS
 
PPTX
Coagulation, flocculation and settling.pptx
byChemical Engineering Dept. NIT Rourkela-769008, Odisha, India
 
PPTX
An Early Production Facility (EPF) is a modular, temporary system for rapidly...
byDrAdelSalem1
 
PPTX
Filtration-slow sand filtration and rapid sand filtration.pptx
byChemical Engineering Dept. NIT Rourkela-769008, Odisha, India
 
PPTX
Exploring Exhaustivity in Wh-Questions Through Analysis of Natural Language U...
byraghabBsingh
 
PDF
Software Engineering : Nature of Software
byGunjalSanjay
 
PPTX
TechSprint WinterHack || After an intense hackathon filled with creativity, ...
bybajpaitusharoffon678
 
lecture 1 Machine tools the introduction
bypushkarkamble2
 
Mahabir - Structural Steel Brochure - 2025
byMahabirIndustries1
 
Julian Kalac -GEN AI inventive solution Automated SOC Report Processing .pdf
byJulian Kalac P.Eng
 
Energy system modelling to support national energy and climate policy making ...
byIEA-ETSAP
 
Hallucination Reduction In Generative Artificial Intelligence (1).docx
by21nitinsinha
 
Earths-Structure-and-Composition_20260127_110958_0000.pdf
byabdurasabarfaki
 
Software Engineering :Software Engineering Practice
byGunjalSanjay
 
Software Engineering : Process Model
byGunjalSanjay
 
LS029B3SX06A 2.9 Inch TFT LCD 2K Resolution 2160X2160 For AR VR
bySyluxdisplay
 
PASSIVE AND ACTIVE REINFORCEMENT LEARNING
byAnushaSanjay
 
Lecture 2 Machine tool - time calculations
bypushkarkamble2
 
Disaster Management Notes for B.Tech. CSE
byhemish04082005
 
BCS402 MICROCONTROLLERS MODULE 1
byAbhijith L Kotian
 
Reality Check Deploying Computer Vision and LLMs at the Edge
byICS
 
Coagulation, flocculation and settling.pptx
byChemical Engineering Dept. NIT Rourkela-769008, Odisha, India
 
An Early Production Facility (EPF) is a modular, temporary system for rapidly...
byDrAdelSalem1
 
Filtration-slow sand filtration and rapid sand filtration.pptx
byChemical Engineering Dept. NIT Rourkela-769008, Odisha, India
 
Exploring Exhaustivity in Wh-Questions Through Analysis of Natural Language U...
byraghabBsingh
 
Software Engineering : Nature of Software
byGunjalSanjay
 
TechSprint WinterHack || After an intense hackathon filled with creativity, ...
bybajpaitusharoffon678
 

Chapter 2 basic structure concepts

  • 1.
    Chapter 2 Basic StructureConcepts January2015 1
  • 2.
    2.0 : BASICSTRUCTURE CONCEPT 2.1 Forces 2.2 Equilibrium and Reactions 2.3 Moments 2.4 Stress and Strain 2.5 Elastic and plastic range 2.6 Primary Loads & Secondary Loads January2015 2
  • 3.
    2.1 Forces A forceis that which tends to exert motion, tension or compression on an object. The loads acting on a structure have mass which is usually measured in kilograms(kg). The basic unit of force is the newton (N). The force exerted on a structure by a static load is dependent upon both its mass and the force of gravity. The force exerted by a body as a result of gravity can be described as its weight. F =W= m x g  Therefore, the force exerted by a mass of 1 kg is: F = m x g = 1 x 9.81 =9.81 N @ 0.00981 kN  1 kN = 1000 N January2015 3
  • 4.
    2.1 Forces Scalars andVectors Scalars Vectors Examples: mass, volume force, velocity Characteristics: It has a magnitude It has a magnitude (positive or negative) and direction Addition rule: Simple arithmetic Parallelogram law Special Notation: None Bold font, a line, an arrow or a “carrot” January2015 4
  • 5.
    2.1 Forces Application ofVector Addition There are four concurrent cable forces acting on the bracket. How do you determine the resultant force acting on the bracket ? January2015 5
  • 6.
    2.1 Forces Vector Operations ScalarMultiplication and Division January2015 6
  • 7.
    2.1 Forces Vector AdditionUsing Either the Parallelogram or Triangle Parallelogram Law: Triangle method (always ‘tip to tail’): How do you subtract a vector? How can you add more than two concurrent vectors graphically ? January2015 7
  • 8.
    2.1 Forces Resolution ofa vector “Resolution” of a vector is breaking up a vector into components. It is kind of like using the parallelogram law in reverse. January2015 8
  • 9.
    2.1 Forces  Eachcomponent of the vector is shown as a magnitude and a direction. Cartesian Vector Notation We ‘ resolve’ vectors into components using the x and y axes system  The directions are based on the x and y axes. We use the “unit vectors” i and j to designate the x and y axes. January2015 9
  • 10.
    2.1 Forces For example, F= Fx i + Fy j or F' = F'x i + F'y j The x and y axes are always perpendicular to each other. Together, they can be directed at any inclination. January2015 10
  • 11.
    2.1 Forces Addition ofSeveral Vectors Step 1 is to resolve each force into its components  Step 2 is to add all the x components together and add all the y components together. These two totals become the resultant vector. Step 3 is to find the magnitude and angle of the resultant vector. January2015 11
  • 12.
  • 13.
  • 14.
    2.1 Forces Example 1 Thescrew eye in Figure below is subjected to forces F1 and F2. Determine the magnitude and direction (measured from x- positive axis) of the resultant force. F2= 150 N F1= 100 N10o 15o January2015 14
  • 15.
    2.1 Forces Solution 10o 15o 15o +90o + 10o = 115o R =√(1002 +1502 – (2x 100 x 150 x cos 115 ) = 212.55 N  Sin /150 = sin 115/212.55 Sin  = (sin 115/212.55) x 150  = 39.76o Direction = 15o + 39.76o =54.76o January2015 15
  • 16.
    2.1 Forces Example 2 Determinethe magnitude of the resultant force and its direction, measured clockwise from the positive x-axis Solution a) Resolve the forces in their x-y components. b) Add the respective components to get the resultant vector. c) Find magnitude and angle from the resultant components. January2015 16
  • 17.
    2.1 Forces F1 ={ 15 sin 40° i + 15 cos 40° j } kN = { 9.642 i + 11.49 j } kN F2 = { -(12/13)26 i + (5/13)26 j } kN = { -24 i + 10 j } kN F3 = { 36 cos 30° i – 36 sin 30° j } kN = { 31.18 i – 18 j } kN January2015 17
  • 18.
    2.1 Forces Summing upall the i and j components respectively, we get, FR = { (9.642 – 24 + 31.18) i + (11.49 + 10 – 18) j } kN = { 16.82 i + 3.49 j } kN FR = ((16.82)2 + (3.49)2)1/2 = 17.2 kN  = tan-1(3.49/16.82) = 11.7° January2015 18
  • 19.
    2.1 Forces Example 3 Determinethe magnitude of the resultant force and its direction, measured counterclockwise from the positive x axis Solution a) Resolve the forces in their x-y components. b) Add the respective components to get the resultant vector. c) Find magnitude and angle from the resultant components. January2015 19
  • 20.
    2.1 Forces F1 ={ (4/5) 850 i - (3/5) 850 j } N = { 680 i - 510 j } N F2 = { -625 sin(30°) i - 625 cos(30°) j } N = { -312.5 i - 541.3 j } N F3 = { -750 sin(45°) i + 750 cos(45°) j } N { -530.3 i + 530.3 j } N January2015 20
  • 21.
    2.1 Forces Summing upall the i and j components respectively, we get, FR = { (680 – 312.5 – 530.3) i + (-510 – 541.3 + 530.3) j }N = { - 162.8 i - 521 j } N FR = ((162.8)2 + (521)2) ½ = 546 N = tan–1(521/162.8) = 72.64° or From Positive x axis  = 180 + 72.64 = 253 ° January2015 21
  • 22.
    TUTORIAL 1 (FORCES) Question1 Two forces are applied to an eye bolt fastened to a beam. Determine the magnitude and direction of their resultant. 6 kN 4.5 kN 25o 50o January2015 22
  • 23.
    Question 2 Two forcesP and Q are applied as shown at point A of a hook support. Knowing that P = 60 kN and Q = 100 kN. Determine the magnitude and direction of their resultant. (Ans: R = 150 kN, 76o towards x axis positive) P Q 15o 30o January2015 24
  • 24.
    Question 3 The cablesAB and AD help support pole AC. Knowing that the tension is 500 N in AB and 160 N in AD. Determine the magnitude and direction of the resultant of the forces exerted by cables at A. (Ans: R = 575 N, 113o towards x axis positive) A B C D 2 m 1.5 m 2.5 m January2015 25
  • 25.
    Question 4 Determine theresultant and direction from x-axis positive of the five forces shown in Figure below by the graphical method. (Ans: R = 32.5 kN, = 124o) y x 8 kN 9 kN 4 kN 60o 25 kN 3 kN 15o 30o 20o January2015 26
  • 26.
    Question 5 Determine themagnitude and direction measured counterclockwise from the positive x axis of the resultant force of the three acting on the ring A. Take F1 = 500 N and  = 20o (Ans: R = 1.03 kN, = 87.9o) y x 600 N F1 400 N 30o 3 4 5 January2015 27
  • 27.
    Question 6 Three forcesare applied at the end of the boom O. Determine the magnitude and orientation of the resultant force. (Ans: FR= 485 N, = 37.7o) y x F3 = 200N F2= 250 N F1 = 400 N 45o 3 4 5 January2015 29
  • 28.
    • Question 7 •Two cables are attached to the frame shown in Figure below. Using trigonometry, determine : (a) the required magnitude of the force P if the resultant R of the two forces applied at A is to be vertical. (b) the corresponding magnitude of R. (Ans: 489 N, 738 N) A A 25o 35o 360 N P January2015 30
  • 29.
    2.2 Equilibriumand Reactions Anystructure subjected to loads must be provided with supports to prevent it from moving. The forces generated on the structure by these supports are called reactions. If the structure is in equilibrium (i.e. not moving) then the net forces from the loads and reactions must be zero in all directions. Fx = 0 Fy = 0  M = 0 January2015 31
  • 30.
  • 31.
    Example 1 Determine themagnitudes of F1 and F2 so that particle P is in equilibrium. (Ans: F1 = 435 N, F2 = 171 N) P F1 F2 400 N 3 4 5 30o 60o January2015 33
  • 32.
    Solution The two unknownmagnitudes F1 and F2 can be obtained from the two scalar equations of equilibrium, ∑Fx=0 and ∑Fy = 0. To apply these equations, the x, y axes are established on the free body diagram and forces must be resolved into its x and y components. P F1 F2 400 N 3 4 5 30o 60o 400 cos 30o 400 sin 30o F2 cos 60o F2 sin 60o F1 (4/5) F1 (3/5) January2015 34
  • 33.
    Solution ∑ Fx =0; -400 sin 30o + F1(4/5) –F2sin 60o=0 ∑ Fy =0; 400 cos 30o -F1(3/5) –F2cos 60o=0 (1) (2) Simplify : 0.8 F1 – 0.866 F2 = 200 (3) -0.6 F1 – 0.5 F2 = -346.61 (4) Solving Eqs. (3) & (4) by simultaneous equations to determine F1 & F2. Ans : F1 = 435.08 N F2 = 170.97 N January2015 35
  • 34.
    Applicationof equilibriumconceptsin truss  Atruss is a structure composed of slender members joined together at their end points.  The members commonly used in construction consist of wooden struts or metal bars  The joint connections are usually formed by bolting or welding the ends of the members to a common plate, called a gusset plate, as shown in Fig below. January2015 36
  • 35.
  • 36.
    38 Timber Roof Trusses SteelBridge Trusses January2015
  • 37.
    Example • Determine theforce in each member of the Pratt bridge truss shown. State whether each member is in tension or compression. 6 kN 6 kN 6 kN 4 m 3 m 3 m 3 m 3 m A B C D E F G H January2015 39
  • 38.
    2.3 Moments APPLICATION What isthe net effect of the two forces on the wheel? January2015 40
  • 39.
    APPLICATION What is theeffect of the 30 N force on the lug nut? January2015 41
  • 40.
     The momentof a force about a point or axis provides a measure of the tendency of the force to cause a body to rotate about the point or axis.  This tendency for rotation caused by force is sometimes called a torque, but most often it is called the moment of a force or simply the moment  The magnitude of a moment about a point is the value of the force multiplied by the perpendicular distance from the line of action of the force to the point  M= T = F x d  The unit is Nm or kNm The typical sign convention for moment is that counter-clockwise is considered positive. January2015 42
  • 41.
    Example 1 From Figurebelow, determine the moment of the force about point O. If the moment is increased to 5 kNm, what is the maximum mass can be supported by the diving board? 1.5 m Mass = 250 kg January2015 43
  • 42.
    Solution F = mg =250 (9.81)= 2452.5 N = 2.45 kN 1.5 m Mo = ( 2.45 x 1.5) = 3.68 kNm If Mo = 5 kNm, then new load is Mo = F x d 5 = F x 1.5 F = 3.33 kN = 3333.33 N F = m x g 3333.33 = m x 9.81 m = 339.79 kg F January2015 44
  • 43.
    Example 2 For eachcase illustrated in Figure below, determine the moment of the force about point O. 5O kN 2 m 0.75 m Solution Mo = - (50 x 0.75) = - 37.5 kNm January2015 45
  • 44.
    Example 3 For eachcase illustrated in Figure below, determine the moment of the force about point O. 6O kN 3 m 45o Solution 1 sin 45o Mo = 60 x (1 sin 45o) = 42.43 kNm January2015 46
  • 45.
    Example 4 A 400N force is applied to the frame and  = 20o. Find the moment of the force at A. Solution 400 sin 20o 400 cos 20o MA = (400 sin 20ox 3) + (400 cos 20o x 2) = 1162.18 Nm January2015 47
  • 46.
    Figure above showsa bridge deck, of weight 500 kN, supporting a heavy vehicle weighing 300 kN. Find the value of the support reactions at A and B when the load is in the position shown. Ans: RA = 430 kN, RB = 370 kN Example 5 January2015 48
  • 47.
    Solution 500 kN 5 m 300kN A B 4 m ∑ MA =0 ; ∑ Fy =0 ; RB (10) – ( 300 x 4) – (500 x 5) = 0 RB = 370 kN RA + RB – 300 – 500 = 0 RA = 430 kN January2015 49
  • 48.
    Example 6 Figure showsan anchorage for the cable of a ski- lift, The cable produce a total pull of 220 kN at the top of the anchorage. Determine the support reactions. Ans: RAH = 191 kN, RAV = -196 kN RB = 306 kN January2015 50
  • 49.
    Solution A B 220 cos30o 220 sin 30o RBRAV RAH ∑ MA =0 ; RB (2.7) – ( 220 sin 30o x 1.8) – (220 cos 30o x 3.3) = 0 RB = 306 kN ∑ Fx =0 ; -RAH + 220 cos 30o = 0 RAH = 191kN RAV + RB – 220 sin 30o = 0 RAV = - 196 kN ∑ Fy =0 ; January2015 51
  • 50.
    2.4 Stress andStrain Stress Concept of stress  To obtain distribution of force acting over a sectioned area  Assumptions of material: 1. It is continuous (uniform distribution of matter) 2. It is cohesive (all portions are connected together) Normal stress  Intensity of force, or force per unit area, acting normal to ΔA  Symbol used for normal stress, is σ (sigma) σz = lim ΔA →0 ΔFz ΔA January2015 52
  • 51.
     Tensile stress:normal force “pulls” or “stretches” the area element ΔA  Compressive stress: normal force “pushes” or “compresses” area element ΔA  Shear stress  Intensity of force, or force per unit area, acting tangent to ΔA  Symbol used for normal stress is τ (tau) τzx = lim ΔA →0 ΔFx ΔA τzy = lim ΔA →0 ΔFy ΔA Units (SI system) Newtons per square meter (N/m2) or a pascal (1 Pa = 1 N/m2) kPa = 103 N/m2 (kilo-pascal) MPa = 106 N/m2 (mega-pascal) GPa = 109 N/m2 (giga-pascal) January2015 53
  • 52.
  • 53.
    Example 1 The 80kg lamp is supported by two rods AB and BC as shown in Figure below. If AB has a diameter of 10 mm and BC has a diameter of 8 mm, determine the average normal stress in each rod. A B C 60o 3 4 January2015 55
  • 54.
    A B C 60o 3 4 F = mg =80 x 9.81 = 784.8 N = 0.78 kN F1 F2 F1cos 60o F1sin 60o F2cos  F2sin  Solution January2015 56
  • 55.
    Solution ∑ Fx =0; – F1cos 60o + F2(4/5) =0 ∑ Fy =0; F1sin 60o+ F2(3/5) – 0.78 =0 (1) (2) Simplify : - 0.5 F1 + 0.8 F2 = 0 (3) 0.866 F1 + 0.6 F2 = 0.78 (4) Solving Eqs. (3) & (4) by simultaneous equations to determine F1 & F2. 0.6 x Eqs (3) - 0.3 F1 + 0.48 F2 = 0 0.8 x Eqs (4) 0.69 F1 + 0.48 F2 = 0.624 - 0.99 F1 = - 0.624 F1 = 0.63 kN Subs F1 into Eqs (3) - - 0.5 F1 + 0.8 F2 = 0 - 0.5 x 0.63 + 0.8 F2 = 0 F2 = 0.315/0.8 = 0.39 kN January2015 57
  • 56.
    Solution 1 = F1/ A1 = 0.63 /( x 0.0052) = 8021.41 kN/m2 2 = F2 / A2 = 0.39/( x 0.0042) = 7758.8 kN/m2 January2015 58
  • 57.
    Shear Stress  Shearstress is the stress component that act in the plane of the sectioned area.  Consider a force F acting to the bar  For rigid supports, and F is large enough, bar will deform and fail along the planes identified by AB and CD  Free-body diagram indicates that shear force, V = F/2 be applied at both sections to ensure equilibrium January2015 59
  • 58.
    Average shear stressover each section is: P Aavg = avg = average shear stress at section, assumed to be same at each pt on the section V = internal resultant shear force at section determined from equations of equilibrium A = area of section January2015 60
  • 59.
    Example 1 The barshown in Figure below has a square cross section for which the depth and thickness are 40 mm. If an axial force of 800 N is applied along the centroidal axis of the bar’s cross-sectional area, determine average normal stress and average shear stress acting on the material along section planes a-a. January2015 61
  • 60.
    Internal loading Based onfree-body diagram, Resultant loading of axial force, P = 800 N Average normal stress = P/A = 800/(0.04)(0.04) = 500 kPa Average shear stress No shear stress exists on the section, since the shear force at the section is zero. January2015 62
  • 61.
    Example 2 Three platesare held together by two cyclindrical rivets. If a direct pull of 5 kN is applied between one plate and the other two, estimate the diameter of the rivets. The shear stress in the rivets is not to exceed 40 N/mm2. 5 kN January2015 63
  • 62.
    Solution • 4 slidingareas (Double shear) P A = 40 = 5000 4(2/4)  = 6.3 mm January2015 64
  • 63.
    Question 1 A 50kN axial load is applied to a short wooden post which is supported by a square concrete footing resting on distributed soil. Determine (a) The maximum bearing stress on the concrete footing (b) The size of the footing for which the average bearing stress on the soil is 150 kPa. (Ans: B = 4MPa, b= 577 mm) Plan 125 mm 100 mm b b 50 kN January2015 65 TUTORIAL 2 (STRESS
  • 64.
    Question 2 The columnis subjected to an axial force of 8 kN at its top. If the cross sectional area has the dimensions shown in the figure, determine the average normal stress at section a-a. (Ans:  = 1.74 MPa) Plan Front Elevation 160 mm 160 mm a a 10 mm 10mm 10 mm 8 kN 160mm January2015 66
  • 65.
    Question 3 The 20kg lamp is supported by two steel rods connected by a ring A. Determine which rod is subjected to the greater average normal stress and compute its value. (Ans:  = 2.33 N/mm2) B A C 60o 45o 12 mm 10 mm January2015 67
  • 66.
    Question 4 A squarehole having 12 mm sides is to be punched out of a metal plate 1.6 mm thick. The shear stress required to cause fracture is 350 N/mm2. What force must be applied to punch die? What would be the compressive stress in the punch? (Ans: 26.88 kN, 0.19 kN/mm2) January2015 68
  • 67.
    ALLOWABLE STRESS  Whendesigning a structural member or mechanical element, the stress in it must be restricted to safe level  Choose an allowable load that is less than the load the member can fully support  One method used is the factor of safety (F.S.) F.S. = Ffail Fallow  If load applied is linearly related to stress developed within member, then F.S. can also be expressed as: F.S. = σfail σallow F.S. = fail allow  In all the equations, F.S. is chosen to be greater than 1, to avoid potential for failure  Specific values will depend on types of material used and its intended purpose January2015 69
  • 68.
    Strain  Loads causebodies to deform, thus points in the body will undergo displacements or changes in position  Normal strain () is a measure of elongation or contraction of small line segment in the body Normal Strain () = Change in length = L Original length L  Has no unit  Shear strain () is a measure of the change in angle that occurs between two small line segments that are originally perpendicular to each other. Shear Strain () = x L L x January2015 70
  • 69.
    Conventional stress-strain diagram Figure shows the characteristic stress-strain diagram for steel, a commonly used material for structural members and mechanical elements January2015 71
  • 70.
    Elastic behavior.  Astraight line  Stress is proportional to strain, i.e., linearly elastic  Upper stress limit, or proportional limit; σpl  If load is removed upon reaching elastic limit, specimen will return to its original shape January2015 72
  • 71.
    Yielding.  Material deformspermanently; yielding; plastic deformation  Yield stress, σY  Once yield point reached, specimen continues to elongate (strain) without any increase in load  Note figure not drawn to scale, otherwise induced strains is 10-40 times larger than in elastic limit  Material is referred to as being perfectly plastic January2015 73
  • 72.
    Strain hardening.  Ultimatestress, σu  While specimen is elongating, its x- sectional area will decrease  Decrease in area is fairly uniform over entire gauge length January2015 74
  • 73.
    Necking.  At ultimatestress, x-sectional area begins to decrease in a localized region  As a result, a constriction or “neck” tends to form in this region as specimen elongates further  Specimen finally breaks at fracture stress, σf January2015 75
  • 74.
    Hooke’s Law When amaterial is worked within its elastic limit, the extension is proportional to the force. Strain  Stress Stress = Constant (E) Strain This constant is known as the modulus of elasticity or Young’s Modulus January2015 76
  • 75.
    Example 1 A tie-barin a steel structure is of rectangular section 30 mm x 50 mm. The extension measured in a 250 mm length of the tie bar when load is applied to the structure is 0.1 mm. Find :- i) The tensile stress in the bar ii) The tensile force iii) The factor of safety used Take E = 205 kN/mm2 and Ultimate stress = 460 N/mm2 January2015 77
  • 76.
    Solution i) The tensilestress in the bar E = stress/strain Strain (ε) = ∆L/L = 0.1/250 = 4 x 10-4 E = stress/strain 205 = / 4 x 10-4  = 205 x 4 x 10-4 = 0.082 kN/mm2 = 82 N/mm2 ii) The tensile force  = F/A 82 = F/(30 x 50) F = 82 x (30 x 50) = 123,000 = 123 kN iiii) The factor of safety used F.S. = Ultimate stress/ Tensile stress = 460 /82 = 5.6 January2015 78
  • 77.
    Example 2 The ultimatestress for a steel is 450 N/mm2. What is the maximum load which a rod 50 mm diameter can carry with a factor of safety of 5? If the rod is 1.5 m long, determine the extension under this loading.( E = 200 kN/mm2.) Solution The factor of safety F.S. = Ultimate stress/ Tensile stress 5 = 450 / tensile stress Tensile stress = 450/5 = 90 N/mm2  = F/A 90 = F/(π r2) F = 90 x (π x 252) = 176,714.59 N = 176.71 kN January2015 79
  • 78.
    Solution The tensile stressin the bar E = stress/strain 200 x 103 = 90/ ε ε = 90/ 200 x 103 = 4.5 x 10-4 Strain (ε) = ∆L/L 4.5 x 10-4 = ∆L/1500 ∆L = 0.675 mm January2015 80
  • 79.
    Exercise 1 A flatsteel tie-bar 4.5 m long, is found to be 2.4mm short. It is sprung into place by means of drafts driven into holes in the end of the bar. Determine: (a) the stress in the bar (b) the factor of safety if the material of the tie-bar has an ultimate stress of 450 N/mm2. Take E for the material as 205 kN/mm2. ( Ans: 109.3 N/mm2, 4.117) January2015 81 TUTORIAL 3 (STRESS, STRAIN & FACTOR OF SAFETY)
  • 80.
    Exercise 2 A metaltube of outside diameter 75 mm and length 1.65 m is to carry a compressive load of 60 kN. If the allowable axial stress is 75 N/mm2 , calculate the inside diameter of the tube. If E of the material is 90 kN/mm2., by how much will the tube shorten under this load? Ans: 67.87 mm, 1.375 mm) January2015 82
  • 81.
    2.5 PrimaryLoads &Secondary Loads  DEADLOADS Dead Loads are those loads which are considered to act permanently; they are "dead," stationary, and unable to be removed. The self-weight of the structural members normally provides the largest portion of the dead load of a building. This will clearly vary with the actual materials chosen. Permanent non-structural elements such as roofing, concrete, flooring, pipes, ducts, interior partition walls, Environmental Control Systems machinery, elevator machinery and all other construction systems within a building must also be included in the calculation of the total dead load. These loads are represented by the red arrow in the illustration. Primary Loads are divided into three broad categories according to the way in which they act upon the structure or structural element. These are DEAD LOADS, LIVE LOADS(IMPOSED LOADS) and WIND LOADS January2015 83
  • 82.
    2.5PrimaryLoads Unit weights ofvarious building materials (kN/m3) Materials Unit Weight Aluminium 24 Bricks 22* Concrete 24 Concrete blocks (lightweight) 12* Concrete blocks (dense) 22* Glass fibre composite 18 Steel 70 Timber 6* * Subject to considerable variation January2015 84
  • 83.
    2.5 PrimaryLoads Unit weightsof various sheet materials (kN/m2) The dead load of a floor or a roof is generally evaluated for one square meter of floor or roof area Sheet materials kN/m2 Acoustic ceiling tiles 0.1 Asphalt (19 mm) 0.45 Aluminium roof sheeting 0.04 Glass (single glazing) 0.1 Plaster (per face of wall) 0.3 Plasterboard 0.15 Rafters, battens and felt 0.14 Sand/cement screed (25 mm) 0.6 Slates 0.6 Steel roof sheeting 0.15 Timber floorboards 0.15 Vinyl Tiles 0.05 January2015 85
  • 84.
    • LIVE LOADS LiveLoads are not permanent and can change in magnitude. They include items found within a building such as furniture, pianos, safes, people, books, cars, computers, machinery, or stored materials, as well as environmental effects such as loads due to the sun, earth or weather. • WIND LOADS Wind and earthquakes loads are put into the special category of lateral live loads due to the severity of their action upon a building and their potential to cause failure. January2015 86
  • 85.
    Secondary loads Structures canbe subjected to secondary loads from temperature changes, shrinkage of members and settlement of supports. January2015 87
  • 86.
    Example 1 Figure showsa precast concrete Beam which is 10.5 m long. a) Calculate the weight of the beam per unit length in kN/m b) Calculate the total weight of the beam January2015 88
  • 87.
    Solution a) Cross sectionalarea of the beam = (0.6 x 0.25) – (0.4 x 0.15) = 0.09 m2 Unit weight of concrete = 24 kN/m3 Weight per unit length = 0.09 x 24 = 2.16 kN/m b) Total weight of the beam = 2.16 x 10.5 = 22.68 kN January2015 89
  • 88.
    Example 2 The floorin a multi-storey office. Building consists of the following: • Vinyl tiles • 40 mm sand/cement screed • 125 mm reinforced concrete slab • Acoustic tile suspended ceiling Determine the dead load in kN/m2 January2015 90
  • 89.
    Solution From the tablegiven • Vinyl tiles = 0.05 • 40 mm sand/cement screed = 0.6 x (40/25) = 0.96 • 125 mm reinforced concrete = 0.125 x 24 = 3.00 slab • Acoustic tile suspended ceiling = 0.10 The dead load = 4.11 kN/m2 January2015 91
  • 90.
    Exercise 1 Figure showsthe outer wall of a multi-storey building which is supported on a beam at each floor level. The wall consist of a 1.2 m height of cavity wall supporting 1.3 m high double glazing. The cavity wall construction is 102.5 mm of brickwork, a 75 mm cavity and 100 mm of plastered lightweight concrete blockwork. Determine the dead load on one beam in kN/m of beam. (Ans: 4.77 kN/m) January2015 92 TUTORIAL 4 (LOADS)