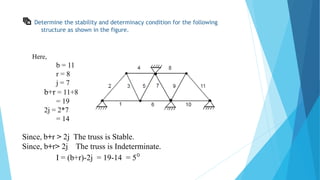
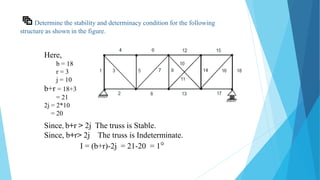
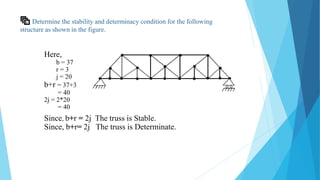
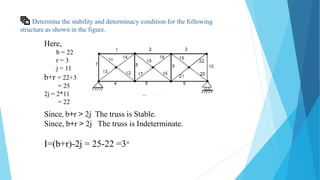
This document introduces different parts of a truss including joints, members, and reactions. It then provides the essential formulas for determining the stability and determinacy of trusses based on the number of joints (j), members (b), and reactive components (r). The remainder of the document works through examples of truss structures, calculating values for b, r, and j, and determining in each case whether the truss is stable/unstable and determinate/indeterminate based on the formulas.

1. M.S MAHAFUZ SHAWON FAKIR
B.Sc. In Civil Engineering.
ID..050 07732
STAMFORD UNIVERSITY BANGLADESH

2. TRUSS
CHAPTER:2

3. INTRODUCE DIFFERENT PART OF THE TRUSS.
 Joint
 Member
Reaction
 Here,
j = Total Number of Joints.
b = Total Number of Member.
r = Minimum Number of Reactive Components
required for External Stability/Determinacy.
 b + r = 2j

4. ESSENTIAL FORMULA FOR TRUSS.
 STABILITY
 b + r < 2J The truss is Stable.
 b + r ≥ 2J The truss is Unstable.
 DETERMINACY:
 b + r = 2J The truss is Determinate.
 b + r > 2J The truss is Indeterminate.
 If truss is Indeterminate, then
Degree of Indeterminacy (I) = (b+r)-2j

5. Determine the stability and determinacy condition for the following
structure as shown in the figure.
Here,
b = 11
r = 8
j = 7
b+r = 11+8
= 19
2j = 2*7
= 14
Since, b+r > 2j The truss is Stable.
Since, b+r> 2j The truss is Indeterminate.
I = (b+r)-2j = 19-14 = 5°

6. Determine the stability and determinacy condition for the following
structure as shown in the figure.
Here,
b = 18
r = 3
j = 10
b+r = 18+3
= 21
2j = 2*10
= 20
Since, b+r > 2j The truss is Stable.
Since, b+r> 2j The truss is Indeterminate.
I = (b+r)-2j = 21-20 = 1°

7. Determine the stability and determinacy condition for the following
structure as shown in the figure.
Here,
b = 17
r = 3
j = 10
b+r = 17+3
= 20
2j = 2*10
= 20
Since, b+r = 2j The truss is Stable.
Since, b+r= 2j The truss is Determinate.

8. Determine the stability and determinacy condition for the following
structure as shown in the figure.
Here,
b = 16
r = 4
j = 9
b+r = 16+4
= 20
2j = 2*9
= 18
Since, b+r < 2j The truss is Unstable.

9. Determine the stability and determinacy condition for the following
structure as shown in the figure.
Here,
b = 9
r = 2
j = 6
b+r = 9+2
= 11
2j = 2*6
= 12
Since, b+r < 2j The truss is Unstable.

10. Determine the stability and determinacy condition for the following
structure as shown in the figure.
Here,
b = 37
r = 3
j = 20
b+r = 37+3
= 40
2j = 2*20
= 40
Since, b+r = 2j The truss is Stable.
Since, b+r= 2j The truss is Determinate.

11. Determine the stability and determinacy condition for the following
structure as shown in the figure.
Here,
b = 14
r = 2
j = 8
b+r = 14+2
= 16
2j = 2*8
= 16
Since, b+r = 2j The truss is Stable.
Since, b+r= 2j The truss is Determinate.

12. Determine the stability and determinacy condition for the following
structure as shown in the figure.
Here,
b = 54
r = 3
j = 25
b+r = 54+3
= 57
2j = 2*25
= 50
Since, b+r > 2j The truss is Stable.
Since, b+r > 2j The truss is Determinate.
I=(b+r)-2j = 57-50 =7°

13. Determine the stability and determinacy condition for the following
structure as shown in the figure.
Here,
b = 22
r = 3
j = 11
b+r = 22+3
= 25
2j = 2*11
= 22
Since, b+r > 2j The truss is Stable.
Since, b+r > 2j The truss is Indeterminate.
I=(b+r)-2j = 25-22 =3°

14. Determine the stability and determinacy condition for the following
structure as shown in the figure.
Here,
b = 13
r = 4
j = 8
b+r = 13+4
= 17
2j = 2*8
= 16
Since, b+r > 2j The truss is Stable.
Since, b+r > 2j The truss is Indeterminate.
I=(b+r)-2j = 17-16 =3°

15. SLAID MADE BY MSF
END