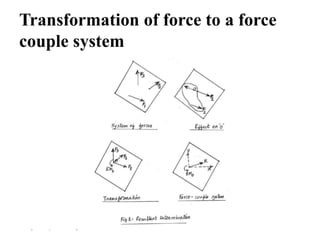
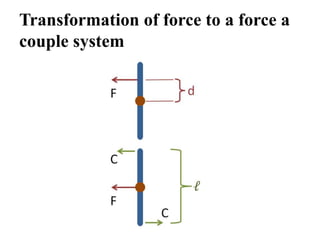
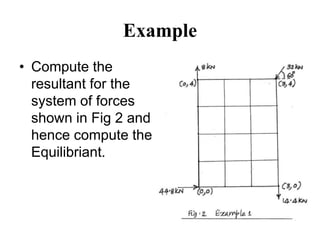
The document discusses non-concurrent forces and how to find their resultant. It defines non-concurrent forces as those whose lines of action do not meet at a single point. It provides examples of such forces, like those on a ladder leaning against a wall. The document discusses using graphical and algebraic methods to resolve non-parallel, non-concurrent forces into components. It also addresses calculating the total moment of such force systems to find the resultant force and its location.

1. ATMIYA INSTITUTE OF TECHNOLOGY & SCIENCE
MECHANICAL DEPARTMENT
3rd SEMESTER
COPLANNER & NON-CONCURRENT
FORCES
(MECHANICS OF SOLIDS – 2130003)
PREPARED BY:
Akash Ambaliya (140030119003)
Akshay Amipara (140030119004)
GUIDED BY:
Sagar I. Shah
(Asst. Prof.)
MECH. DEPT.

2. Definition
• All forces do not meet at a
point, but lie in a single
plane.
• An example is a ladder
resting against wall when a
person stands on a rung,
which is not at its centre of
gravity.
• In this case, for equilibrium,
both the conditions of
ladder need to be checked.

3. Definition
• The principles of equilibrium are also used to
determine the resultant of non-parallel, non-
concurrent systems of forces.
• Simply put, all of the lines of action of the
forces in this system do not meet at one point.
• The parallel force system was a special case
of this type.
• Since all of these forces are not entirely
parallel, the position of the resultant can be
established using
the graphical or algebraic methods of
resolving co-planar forces discussed earlier or
the link polygon.

4. Resultant of Non-concurrent Forces
• If we want to replace a set of
forces with a
single resultant force we
must make sure it has not
only the total Fx, Fy but also
the same moment effect
(about any chosen point).
• It turns out that when we add
up the moment of several
forces we get the same
answer as taking the
moment of the resultant.

5. Resultant of Non-concurrent Forces
• To obtain the total moment of a system of
forces, we can either...
– Calculate the moment caused by the resultant
of the system of forces about that point (So
long as the resultant is in the RIGHT PLACE
to create the right rotation).
– Calculate each moment (from each force
separately) and add them up, keeping in mind
the CW and CCW sign convention.

6. Resultant of Non-concurrent Forces
• By using the principles of resolution composition &
moment it is possible to determine analytically the
resultant for coplanar non-concurrent system of forces.
• The procedure is as follows:
– Select a Suitable Cartesian System for the given problem.
– Resolve the forces in the Cartesian System
– Compute fxi and fyi
– Compute the moments of resolved components about any
point taken as the moment
– centre O. Hence find M0

7. Resultant of Non-concurrent Forces

8. Transformation of force to a force
couple system
• It is well known that moment of a force
represents its rotatary effect about an axis or
a point.
• This concept is used in determining the
resultant for a system of coplanar non-
concurrent forces.
• For ay given force it is possible to determine
an equivalent force – couple system.

9. Transformation of force to a force
couple system

10. Transformation of force to a force
couple system
• A force F applied to a rigid body at a
distance d from the centre of mass has the same
effect as the same force applied directly to the
centre of mass and a couple Cℓ = Fd.
• The couple produces an angular acceleration of
the rigid body at right angles to the plane of the
couple.
• The force at the centre of mass accelerates the
body in the direction of the force without change in
orientation.

11. Transformation of force to a force
couple system
• The general theorems are:
– A single force acting at any point O′ of a rigid body can be
replaced by an equal and parallel force F acting at any
given point O and a couple with forces parallel to F whose
moment is M = Fd, d being the separation of O and O′.
• Conversely, a couple and a force in the plane of the
couple can be replaced by a single force, appropriately
located.
• Any couple can be replaced by another in the same
plane of the same direction and moment, having any
desired force or any desired arm.

12. Transformation of force to a force a
couple system

13. Applications of Couple Forces
• Couples are very important in mechanical
engineering and the physical sciences. A few
examples are:
– The forces exerted by one's hand on a screw-
driver
– The forces exerted by the tip of a screw-driver on
the head of a screw
– Drag forces acting on a spinning propeller
– Forces on an electric dipole in a uniform electric
field.
– The reaction control system on a spacecraft.

14. Example
• Compute the
resultant for the
system of forces
shown in Fig 2 and
hence compute the
Equilibriant.

15. Example (Solution)

16. Thank You…