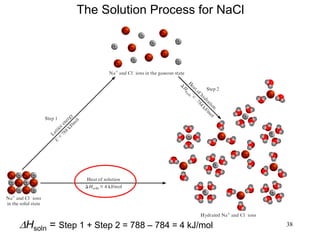
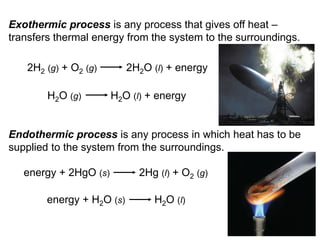
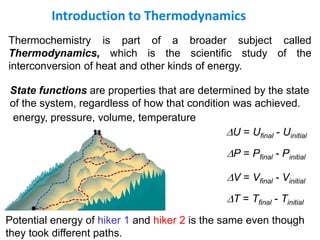
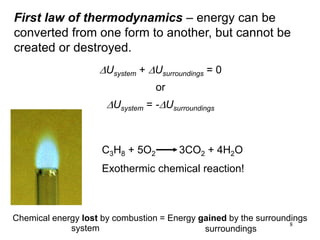
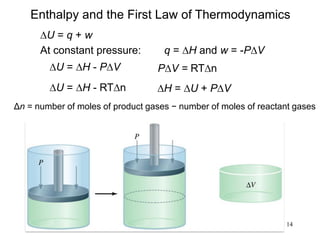
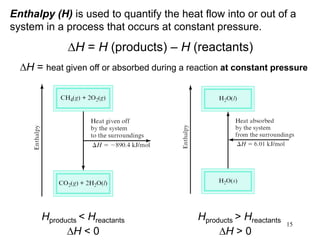
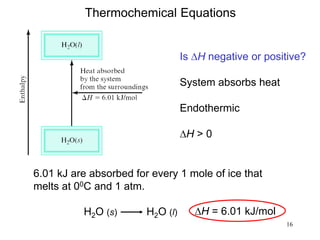
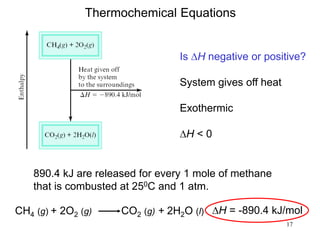
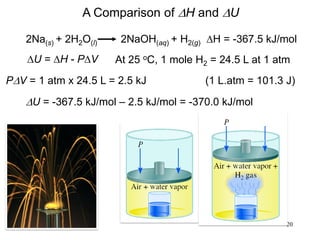
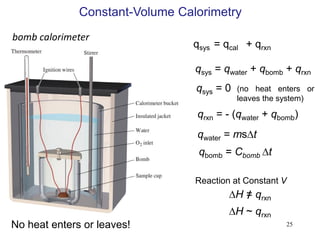
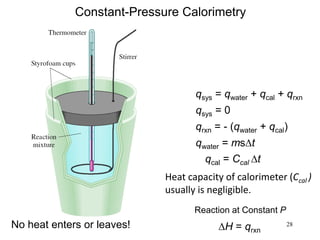
Thermochemistry is the study of heat changes in chemical reactions. There are several types of energy including chemical, thermal, nuclear, and radiant energy. Heat is the transfer of thermal energy between objects at different temperatures. Thermochemistry examines heat absorbed or released by chemical reactions using concepts like exothermic, endothermic, enthalpy, and calorimetry. The first law of thermodynamics states that energy cannot be created or destroyed, only transferred between systems and their surroundings.

1. Thermochemistry
Chapter 6
Dr. Sa’ib Khouri
AUM- JORDAN
Chemistry
By Raymond Chang

2. 2
Energy is the capacity to do work, and unlike matter energy is
known and recognized by its effects (It cannot be seen,
touched, smelled, or weighed)
Kinetic energy was first introduced in ch. 5,
• Radiant energy comes from the sun and is earth’s primary
energy source
• Thermal energy is the energy associated with the random
motion of atoms and molecules
• Chemical energy is the energy stored within the bonds of
chemical substances
• Nuclear energy is the energy stored within the collection of
neutrons and protons in the atom
• Potential energy is the energy available by virtue of an
object’s position
• All forms of energy can be converted from one form to another.

3. 3
Heat is the transfer of thermal energy (energy flow)
between two bodies that are at different temperatures.
Thermochemistry is the study of heat change in
chemical reactions (heat absorbed or heat released)
The system is the specific part of the universe that is
of interest in the study.
The surroundings are the rest of universe outside
the system.
Energy Changes in Chemical Reactions
Temperature is a measure of the thermal energy.
Temperature = Thermal Energy

4. 4
open
mass & energy
Exchange:
closed
energy
isolated
nothing
Three types of systems

5. 5
Exothermic process is any process that gives off heat –
transfers thermal energy from the system to the surroundings.
Endothermic process is any process in which heat has to be
supplied to the system from the surroundings.
2H2 (g) + O2 (g) 2H2O (l) + energy
H2O (g) H2O (l) + energy
energy + 2HgO (s) 2Hg (l) + O2 (g)
energy + H2O (s) H2O (l)

6. 6
Schematic of Exothermic and Endothermic Processes

7. 7
Thermochemistry is part of a broader subject called
Thermodynamics, which is the scientific study of the
interconversion of heat and other kinds of energy.
State functions are properties that are determined by the state
of the system, regardless of how that condition was achieved.
Potential energy of hiker 1 and hiker 2 is the same even though
they took different paths.
energy, pressure, volume, temperature
DU = Ufinal - Uinitial
DP = Pfinal - Pinitial
DV = Vfinal - Vinitial
DT = Tfinal - Tinitial
Introduction to Thermodynamics

8. 8
First law of thermodynamics – energy can be
converted from one form to another, but cannot be
created or destroyed.
DUsystem + DUsurroundings = 0
or
DUsystem = -DUsurroundings
C3H8 + 5O2 3CO2 + 4H2O
Exothermic chemical reaction!
Chemical energy lost by combustion = Energy gained by the surroundings
system surroundings

9. 9
Another form of the first law for DUsystem
DU = q + w
DU is the change in internal energy of a system
q is the heat exchange between the system and the surroundings
w is the work done on (or by) the system
w = -PDV when a gas expands against a constant external pressure

10. 10
Work and Heat
w = F x d (force multiplied by distance)
(The work done by the gas on the surroundings)
w = - P DV
where ΔV, the change in volume, is given by Vf − Vi
1. For gas expansion (work done by the system),
ΔV > 0, so −PΔV is a negative quantity, work has negative sign.
2. For gas compression (work done on the system),
ΔV < 0, and −PΔV is a positive quantity, work has positive sign.
P x V = x d3 = F x d = w
F
d2
w = -P DV
Work is not a state function.
Dw = wfinal - winitial
Work

11. 11
initial final
The successive expansion and compression of the cylinders due to the
combustion of the gasoline-air mixture provide power to the vehicle.
See the figure below
A gas in a cylinder fitted with a weightless, frictionless movable piston
at a certain temperature, pressure, and volume.
As it expands, the gas pushes the piston upward against a constant
opposing external atmospheric pressure P.

12. 12
A sample of nitrogen gas expands in volume from 1.6 L to 5.4 L
at constant temperature. What is the work done in joules if the
gas expands (a) against a vacuum (b) against a constant
pressure of 3.7 atm?
w = -P DV
(a) DV = 5.4 L – 1.6 L = 3.8 L P = 0 atm
W = -0 atm x 3.8 L = 0 L•atm = 0 joules
(b) DV = 5.4 L – 1.6 L = 3.8 L P = 3.7 atm
w = -3.7 atm x 3.8 L = -14.1 L•atm
w = -14.1 L•atm x
101.3 J
1L•atm
= -1430 J
Example

13. 13
Heat
The other component of internal energy is heat, q. Like work, heat is
not a state function. For example, it takes 4184 J of energy to raise the
temperature of 100 g of waterfrom 20°C to 30°C.
Example

14. 14
Enthalpy and the First Law of Thermodynamics
DU = q + w
DU = DH - PDV
DH = DU + PDV
q = DH and w = -PDV
At constant pressure:
PDV = RTDn
DU = DH - RTDn
Δn = number of moles of product gases − number of moles of reactant gases

15. 15
Enthalpy (H) is used to quantify the heat flow into or out of a
system in a process that occurs at constant pressure.
DH = H (products) – H (reactants)
DH = heat given off or absorbed during a reaction at constant pressure
Hproducts < Hreactants
DH < 0
Hproducts > Hreactants
DH > 0

16. 16
Thermochemical Equations
H2O (s) H2O (l) DH = 6.01 kJ/mol
Is DH negative or positive?
System absorbs heat
Endothermic
DH > 0
6.01 kJ are absorbed for every 1 mole of ice that
melts at 00C and 1 atm.

17. 17
Thermochemical Equations
CH4 (g) + 2O2 (g) CO2 (g) + 2H2O (l) DH = -890.4 kJ/mol
Is DH negative or positive?
System gives off heat
Exothermic
DH < 0
890.4 kJ are released for every 1 mole of methane
that is combusted at 250C and 1 atm.

18. 18
H2O (s) H2O (l) DH = 6.01 kJ/mol
• The stoichiometric coefficients always refer to the number
of moles of a substance
Thermochemical Equations
• If you reverse a reaction, the sign of DH changes
H2O (l) H2O (s) DH = -6.01 kJ/mol
• If you multiply both sides of the equation by a factor n,
then DH must change by the same factor n.
2H2O (s) 2H2O (l) DH = 2 x 6.01 = 12.0 kJ

19. 19
H2O (s) H2O (l) DH = 6.01 kJ/mol
• The physical states of all reactants and products must be
specified in thermochemical equations.
Thermochemical Equations
H2O (l) H2O (g) DH = 44.0 kJ/mol
How much heat is evolved when 266 g of white phosphorus (P4)
burn in air?
P4 (s) + 5O2 (g) P4O10 (s) DH = -3013 kJ/mol
266 g P4
1 mol P4
123.9 g P4
x
3013 kJ
1 mol P4
x = 6470 kJ

20. 20
A Comparison of DH and DU
2Na(s) + 2H2O(l) 2NaOH(aq) + H2(g) DH = -367.5 kJ/mol
DU = DH - PDV At 25 oC, 1 mole H2 = 24.5 L at 1 atm
PDV = 1 atm x 24.5 L = 2.5 kJ (1 L.atm = 101.3 J)
DU = -367.5 kJ/mol – 2.5 kJ/mol = -370.0 kJ/mol

21. 21
Example
Calculate the change in internal energy when 2 moles of CO
are converted to 2 moles of CO2 at 1 atm and 25°C:
2CO(g) + O2(g) ⟶2CO2(g) ΔH = −566.0 kJ/mol
Solution
Δn = number of moles of product gases − number of moles of reactant gases
= 2 − 3
= −1
ΔU = ΔH − RTΔn
= −566000 J/mol − (8.314 J/K mol)(298 K)(−1)
= −563500 J/mol
= −563.5 kJ/mol
Practice Exercise What is ΔU for the formation of 1 mole of CO at 1 atm
and 25°C?
C (graphite) +
1
2
O2(g) ⟶ CO(g) ΔH = −110.5 kJ/mol

22. 22

23. 23
calorimetry, the measurement of heat changes, will depend
on an understanding of specific heat and heat capacity.
Calorimetry
The specific heat (s) of a substance is the amount of heat
required to raise the temperature of one gram of the
substance by one degree Celsius. It has the units J/g °C
The heat capacity (C) of a substance is the amount of heat
required to raise the temperature of a given quantity of the
substance by one degree Celsius. Its units are J/°C.
C = ms m: the mass of the substance (g)
e.g. The specific heat of water is 4.184 J/g °C
The heat capacity of 60.0 g of water is
(60.0 g)(4.184 J/g °C) = 251 J/°C

24. 24
Heat (q) absorbed or released in a particular process
q = msΔt
q = CΔt Δt = tfinal − tinitial
e.g.
How much heat is given off when an
869 g iron bar cools from 94oC to 5oC?
s of Fe = 0.444 J/g oC
Dt = tfinal – tinitial = 5oC – 94oC = -89oC
q = msDt
= 869 g x 0.444 J/g oC x –89oC
= -34,000 J
HW. A 466 g sample of water is heated from 8.50°C to 74.60°C.
Calculate the amount of heat absorbed by the water (ans. 129 kJ).
C = ms

25. 25
Constant-Volume Calorimetry
No heat enters or leaves!
qsys = qwater + qbomb + qrxn
qsys = 0
qrxn = - (qwater + qbomb)
qwater = msDt
qbomb = Cbomb Dt
Reaction at Constant V
DH ~ qrxn
DH = qrxn
bomb calorimeter
qsys = qcal + qrxn
(no heat enters or
leaves the system)

26. 26
The quantity Ccal is calibrated by burning a substance with an
accurately known heat of combustion.
e.g. it is known that the combustion of 1 g of benzoic acid
(C6H5COOH) releases 26.42 kJ of heat.
If the temperature rise is 4.673°C
Ccal =
qcal
Δt
=
26.42 kJ
4.673°C
= 5.654 kJ/°C
Once Ccal has been determined, the calorimeter can be used to measure the
heat of combustion of other substances.

27. 27
1.435 g of naphthalene (C10H8), was burned in a constant-volume bomb
calorimeter. The temperature of the water rose from 20.28°C to 25.95°C. If
the heat capacity of the calorimeter was 10.17 kJ/°C, calculate the heat of
combustion of naphthalene sample and the molar heat of combustion.
Example
Example
Solution
qcal = CcalΔt
= (10.17 kJ/°C)(25.95°C − 20.28°C)
= 57.66 kJ
qcal = −qrxn The heat change of the reaction is −57.66 kJ.
This is the heat released by the combustion of 1.435 g of C10H8
The molar mass of naphthalene is 128.2 g, so the heat of
combustion of 1 mole of naphthalene is
Molar heat of combustion = −57.66 kJ
1.435 g C10H8
x
128.2 g C10H8
1 mol C10H8
= −5.151 × 103 kJ/mol

28. 28
Constant-Pressure Calorimetry
No heat enters or leaves!
qsys = qwater + qcal + qrxn
qsys = 0
qrxn = - (qwater + qcal)
qwater = msDt
qcal = Ccal Dt
Reaction at Constant P
DH = qrxn
Heat capacity of calorimeter (Ccal )
usually is negligible.

29. 29
Example (physical change)
A lead (Pb) pellet having a mass of 26.47 g at 89.98°C was placed in a
constant-pressure calorimeter of negligible heat capacity containing 100.0 mL
of water. The water temperature rose from 22.50°C to 23.17°C. What is the
specific heat of the lead pellet?
qPb + qH2O = 0
or qPb = −qH2O
Solution
heat gained by the water
q H2O = msΔt
= (100.0 g)(4.184 J/g °C)(23.17°C − 22.50°C)
= 280.3 J
Because the heat lost by the lead pellet is equal to the heat gained by the water
qPb = −280.3 J
qPb = msΔt
−280.3 J = (26.47 g)(s)(23.17°C − 89.98°C)
s = 0.158 J/g °C

30. 30
A quantity of 100 mL of 0.500 M HCl was mixed with 100 mL of 0.500 M
NaOH in a constant-pressure calorimeter of negligible heat capacity. The
initial temperature of the HCl and NaOH solutions was the same,
22.50°C, and the final temperature of the mixed solution was 25.86°C.
Calculate the heat change for the neutralization reaction on a molar
basis:
NaOH(aq) + HCl(aq) ⟶NaCl(aq) + H2O(l)
Assume that the densities and specific heats of the solutions are the
same as for water (1.00 g/mL and 4.184 J/g °C, respectively).
Example (chemical change)
Solution Assuming no heat is lost to the surroundings, qsys = qsoln + qrxn = 0,
so qrxn = −qsoln
qsoln= msΔt
= (100g + 100g)(4.184 J/g °C)(25.86°C − 22.50°C)
= 2810 J
= 2.81 kJ Because qrxn = −qsoln, qrxn = −2.81 kJ
# of moles of HCl or NaOH in 100 mL (0.100 L) solution is 0.0500 mol
Heat of neutralization =
−2.81 kJ
0.0500 mol
= −56.2 kJ/mol

31. 31
Table 6.3 lists some reactions that have been studied with the
constant-pressure calorimeter.

32. 32
Because there is no way to measure the absolute value of
the enthalpy of a substance, the enthalpy change for every
reaction of interest can be determined.
Establish an arbitrary scale with the standard enthalpy of
formation (DH0) as a reference point for all enthalpy
expressions.
f
Standard enthalpy of formation (DH0) is the heat change
that results when one mole of a compound is formed from
its elements at a pressure of 1 atm.
f
The standard enthalpy of formation of any element in its
most stable form is zero.
DH0 (O2) = 0
f
DH0 (O3) = 142 kJ/mol
f
DH0 (C, graphite) = 0
f
DH0 (C, diamond) = 1.90 kJ/mol
f
Standard Enthalpy of Formation and Reaction

33. 33

34. 34
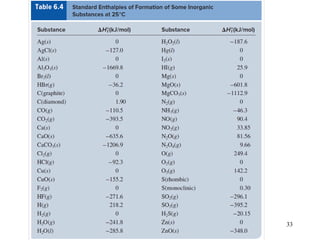
The standard enthalpy of reaction (DH0 ) is the enthalpy of
a reaction carried out at 1 atm.
rxn
aA + bB cC + dD
DH0
rxn dDH0 (D)
f
cDH0 (C)
f
= [ + ] - bDH0 (B)
f
aDH0 (A)
f
[ + ]
DH0
rxn nDH0 (products)
f
= S mDH0 (reactants)
f
S
-
Hess’s Law: When reactants are converted to products, the
change in enthalpy is the same whether the reaction takes
place in one step or in a series of steps.
(Enthalpy is a state function. It doesn’t matter how you get
there, only where you start and end.)
where m and n denote the stoichiometric coefficients for the reactants
and products

35. 35
Example: Calculate the standard enthalpy of formation (DH0
f) of
CS2 (l) given that:
C(graphite) + O2 (g) CO2 (g) DH0 = -393.5 kJ/mol
rxn
S(rhombic) + O2 (g) SO2 (g) DH0 = -296.1 kJ/mol
rxn
CS2(l) + 3O2 (g) CO2 (g) + 2SO2 (g) DH0 = -1072 kJ/mol
rxn
1. Write the enthalpy of formation reaction for CS2
C(graphite) + 2S(rhombic) CS2 (l)
2. Add the given rxns so that the result is the desired rxn.
rxn
C(graphite) + O2 (g) CO2 (g) DH0 = -393.5 kJ/mol
2S(rhombic) + 2O2 (g) 2SO2 (g) DH0 = -296.1 kJ/mol x 2
rxn
CO2(g) + 2SO2 (g) CS2 (l) + 3O2 (g) DH0 = +1072 kJ/mol
rxn
+
C(graphite) + 2S(rhombic) CS2 (l)
DH0 = -393.5 + (2x-296.1) + 1072 = 86.3 kJ/mol
rxn

36. 36
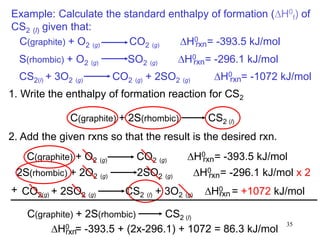
Example: Benzene (C6H6) burns in air to produce carbon
dioxide and liquid water. How much heat is released per mole
of benzene combusted? The standard enthalpy of formation of
benzene is 49.04 kJ/mol.
2C6H6 (l) + 15O2 (g) 12CO2 (g) + 6H2O (l)
DH0
rxn nDH0 (products)
f
= S mDH0 (reactants)
f
S
-
DH0
rxn 6DH0 (H2O)
f
12DH0 (CO2)
f
= [ + ] - 2DH0 (C6H6)
f
[ ]
DH0
rxn = [ 12x–393.5 + 6x–187.6 ] – [ 2x49.04 ] = -5946 kJ
-5946 kJ
2 mol
= - 2973 kJ/mol C6H6

37. 37
The enthalpy of solution (DHsoln) is the heat generated or
absorbed when a certain amount of solute dissolves in a
certain amount of solvent. DHsoln = Hsoln - Hcomponents
Which substance(s) could be used
for melting ice?
Which substance(s) could be used
for a cold pack?
Hsoln : enthalpy of the final solution
Hcomponents : enthalpies of its original components (that is, solute and solvent)
before they are mixed
Neither Hsoln nor Hcomponents can be
measured, but their difference, ΔHsoln, can
be readily determined in a constant-
pressure calorimeter.

38. 38
The Solution Process for NaCl
DHsoln = Step 1 + Step 2 = 788 – 784 = 4 kJ/mol

39. 39
ΔHsoln = U + ΔH hydr
Applying Hess’s law, it is possible to consider ΔHsoln as the
sum of two related quantities, lattice energy (U) and heat of
hydration (ΔHhydr), as shown in the Figure:
When 1 mole of NaCl dissolves in water, 4 kJ of heat will be
absorbed from the surroundings.

40. 40
Example: heat of solution
An 11.0 g sample of CaCl2 is dossplved in 125.0 g water at 25.0 oC,
calculate the heat of solution of CaCl2 if the final temperature reached 40.5
oC assuming no heat loss to the surroundings and assuming the solution
has a specific heat of 4.184 J/g oC.
qCaCl2
+ qH2O = 0
or qCaCl2
= −qH2O
Solution
heat gained by the water
q H2O = msΔt
= (125.0 g)(4.184 J/g °C)(40.5°C − 25.0°C)
= 8106.5 J Because qCaCl2
= −qH2O, qCaCl2
= − 8106.5 J
# of moles CaCl2 (11.0 g/111 g/mol) = 0.0991 mol
Heat of solution of CaCl2 =
− 8106.5 J
0.0991 mol
= −81801.2 J/mol (or −81.80 kJ/mol)

41. 41