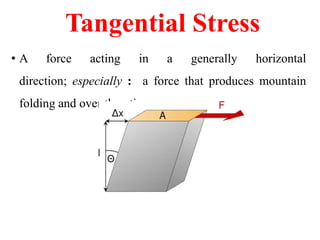
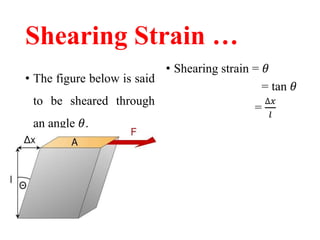
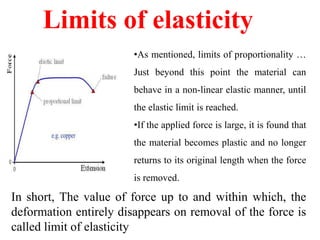
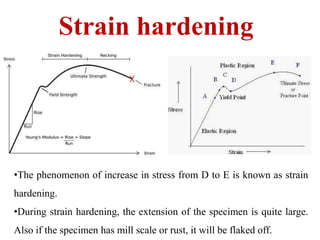
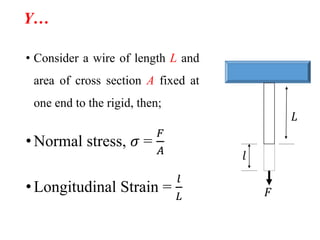
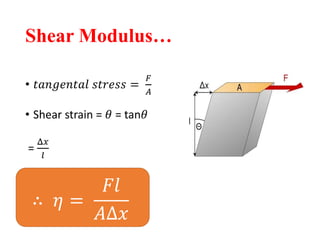
The document discusses the principles of strength of materials, including definitions and properties of rigid and deformable bodies, stress and strain, as well as various types of stress and their applications in structural analysis. It also covers elasticity, different modulus types, and phenomena such as yielding, strain hardening, and Poisson's ratio, along with practical examples and calculations related to these concepts. Overall, it serves as a comprehensive overview of material strength and its implications in engineering.

1. Peter Huruma Mammba
Department of General Studies
DODOMA POLYTECHNIC OF ENERGY AND EARTH RESOURCES
MANAGEMENT (MADINI INSTITUTE) –DODOMA
peter.huruma2011@gmail.com
STREGHTH OF
MATERIALS

2. Strength Of Materials :
• Strength of materials, also called Mechanics of
materials, is a subject which deals with the behavior
of solid objects subject to stresses and strains.
• The study of strength of materials often refers to
various methods of calculating the stresses and strains
in structural members, such as beams, columns, and
shafts.

3. Rigid Body:
• A rigid body is defined as a body on which
the distance between two points never
changes whatever be the force applied on it.
• Practically, there is no rigid body.

4. Deformable body:
A deformable body is defined as a body on which the distance between
two points changes under action of some forces when applied on it.
The study of the property of this body is called Elasticity

5. Elasticity
• The property of a body by virtue of which it
tends to regain its original shape and size
when deforming force is removed .
• All solids show the property of elasticity.

6. Stress (𝝈):
Stress is the applied force or system of forces
that tends to deform a body.

7. Stress…
• 𝑆𝑡𝑟𝑒𝑠𝑠 =
𝐸𝑥𝑡𝑒𝑟𝑛𝑎𝑙 𝑑𝑒𝑓𝑜𝑟𝑚𝑖𝑛𝑔 𝑓𝑜𝑟𝑐𝑒
𝐴𝑟𝑒𝑎
=
𝐹
𝐴
• Dimensional formula of the stress =
𝑀𝐿𝑇−2
𝐿2
∴ = 𝑀𝐿−1
𝑇−2
• The SI unit of stress is 𝑁𝑚−2
= 𝑃𝑎 𝑠𝑐𝑎𝑙
Same as that of pressure

8. Types of Stress…
• The stress developed in a body depends upon
how the external forces are applied over it. On
this basis, there are two types of stress ,
i. Normal Stress
ii. Tangential Stress

9. Normal Stress
• Is a stress that occurs when the surface of the body
is loaded by an axial force.
• Normal stress is of two types;
i. Tensile stress
ii. Compressive stress

10. Tensile stress:
• Is the stress state leading to expansion; that is, the
length of a material tends to increase in the tensile
direction.
This is an example
of tensile stress
tester (Universal
Testing Machine)

11. Ductile behavior:
• Ductility is a solid material's ability to deform under
tensile stress.
Copper wires

12. Compressive stress:
• A force that attempts to squeeze or compress a material.
• Here, the Universal Testing Machine (UTM) is testing a
concrete block.

13. Tangential Stress
• A force acting in a generally horizontal
direction; especially : a force that produces mountain
folding and over thrusting

14. Brittle behavior:
• A material is brittle if, when subjected to stress,
it breaks without insignificant deformation.
• Glass is a good example.

15. Strain (𝜺)
• Is the change in the size or shape of a body due to
the deforming force.Type equation here.
• i.e.
𝑆𝑡𝑟𝑎𝑖𝑛, =
𝐶ℎ𝑎𝑛𝑔𝑒 𝑖𝑛 𝐷𝑖𝑚𝑒𝑛𝑠𝑖𝑜𝑛
𝑂𝑟𝑖𝑔𝑖𝑛𝑎𝑙 𝑑𝑖𝑚𝑒𝑛𝑠𝑖𝑜𝑛
• Strain is Dimensionless hence no unit

16. Types of Strain;
• Since the deforming force can produce three of
deformations (i.e. Change in length, or volume
or shape) in a body, there are three types of
strain;
i. Longitudinal strain
ii. Volumetric strain
iii. Shearing strain

17. Longitudinal Strain
• Is when the deforming force produces change in
length.
• 𝐿𝑜𝑛𝑔𝑖𝑡𝑢𝑑𝑖𝑛𝑎𝑙 𝑆𝑡𝑟𝑎𝑖𝑛 =
𝐶ℎ𝑎𝑛𝑔𝑒 𝑖𝑛 𝐿𝑒𝑛𝑔𝑡ℎ
𝑂𝑟𝑖𝑔𝑖𝑛𝑎𝑙 𝐿𝑒𝑛𝑔𝑡ℎ
=
𝑙
𝐿
∴ long =
𝑙
𝐿

18. Volumetric Strain
• Is when the deforming force produces change
in the volume.
𝑉𝑜𝑙𝑢𝑚𝑒𝑡𝑟𝑖𝑐 𝑆𝑡𝑟𝑎𝑖𝑛 =
𝐶ℎ𝑎𝑛𝑔𝑒 𝑖𝑛 𝑉𝑜𝑙𝑢𝑚𝑒
𝑂𝑟𝑖𝑔𝑖𝑛𝑎𝑙 𝑉𝑜𝑙𝑢𝑚𝑒
=
∆𝑉
𝑉
∴ vol =
∆𝑉
𝑉

19. Shearing Strain
• Is when the deforming force produces change
in the shape of the body.
• It is measured by the angle 𝜃 (in radian)
through which a line originally perpendicular to
the fixed face is turned due to the application of
the tangential force.

20. Shearing Strain …
• The figure below is said
to be sheared through
an angle 𝜃.
• Shearing strain = 𝜃
= tan 𝜃
=
∆𝑥
𝑙

21. Elasticity
• Elasticity is the tendency of solid materials to return to their
original shape after being forces are applied on them.
• When the forces are removed, the object will return to its initial
shape and size if the material is elastic.
• In other words, The deformation disappears completely, after
removal of external forces.
• Steel cables, rubber bands, springs are the examples of the elastic
materials.

22. Elastic Limit
• Is the maximum stress from which an elastic
body will recover its original state after the
removal of the deforming force.
• It differs widely for different materials.
• It is very high for a substance like steel and low
for a substance like lead.

23. Limits of proportionality
•If a tensile force applied to a uniform bar
of mild steel is gradually increased and the
corresponding extension of the bar is
measured, then provided the applied force
is not too large, a graph depicting these
results is likely to be as shown in Figure.
•Since the graph is a straight line,
extension is directly proportional to the
applied force. (Hooke’s Law)
The point on the graph where extension is no longer proportional
to the applied force is known as the limit of proportionality.

24. Limits of elasticity
•As mentioned, limits of proportionality …
Just beyond this point the material can
behave in a non-linear elastic manner, until
the elastic limit is reached.
•If the applied force is large, it is found that
the material becomes plastic and no longer
returns to its original length when the force
is removed.
In short, The value of force up to and within which, the
deformation entirely disappears on removal of the force is
called limit of elasticity

25. Yield limit •When specimen is stressed beyond
elastic limit, strain increases more
rapidly than the stress. Because, sudden
elongation of the specimen takes place,
without appreciable increase in the
stress. This phenomena is known as
yielding of material.
• The stress corresponding to point of upper yield point is
called yield stress.
• The portion between upper yield point and lower yield
point is called yield stage.

26. Ultimate stress
•Because of the plastic deforms,
the material strain hardens and
further strain beyond lower yield
point requires an increase in
stress.
•The maximum stress reached at
point E is called ultimate stress.
•In other words, Stress
corresponding to the maximum
load taken by the specimen is
called ultimate stress.

27. Strain hardening
•The phenomenon of increase in stress from D to E is known as strain
hardening.
•During strain hardening, the extension of the specimen is quite large.
Also if the specimen has mill scale or rust, it will be flaked off.

28. Modulus of Elasticity
• Young's modulus, also known as the tensile
modulus or elastic modulus, is a measure of
the stiffness of an elastic material.
• Named after a British Scientist THOMAS
YOUNG

29. Thomas Young:

30. Modulus of Elasticity
• 𝑆𝑡𝑟𝑒𝑠𝑠 ∝ 𝑆𝑡𝑟𝑎𝑖𝑛
Or
𝑺𝒕𝒓𝒆𝒔𝒔
𝑺𝒕𝒓𝒂𝒊𝒏
= 𝑪𝒐𝒏𝒔𝒕𝒂𝒏𝒕 = 𝑴𝒐𝒅𝒖𝒍𝒖𝒔 𝒐𝒇 𝒆𝒍𝒂𝒔𝒕𝒊𝒄𝒊𝒕𝒚
Its unit is “pa” or N/m2
NB: If the modulus of elasticity of a material is large,
it means a larger stress will produce only a small
strain.

31. Types of Modulus of Elasticity
• Corresponding to three types of strain, there are
three moduli of elasticity;
i. Young’s Modulus of elasticity, Y
ii. Bulk modulus of elasticity, K =
𝑁𝑜𝑟𝑚𝑎𝑙 𝑠𝑡𝑟𝑒𝑠𝑠
𝑉𝑜𝑙𝑢𝑚𝑒𝑡𝑟𝑖𝑐 𝑠𝑡𝑟𝑎𝑖𝑛
iii. Modulus of rigidity, 𝜂 =
𝑆ℎ𝑒𝑎𝑟𝑖𝑛𝑔 𝑠𝑡𝑟𝑒𝑠𝑠
𝑆ℎ𝑒𝑎𝑟𝑖𝑛𝑔 𝑠𝑡𝑟𝑎𝑖𝑛

32. Young’s Modulus (Y)
• It is defined as the ratio of normal stress to
the longitudinal strain.
Y =
𝑁𝑜𝑟𝑚𝑎𝑙 𝑠𝑡𝑟𝑒𝑠𝑠
𝐿𝑜𝑛𝑔𝑖𝑡𝑢𝑑𝑖𝑛𝑎𝑙 𝑠𝑡𝑟𝑎𝑖𝑛

33. Y…
• Consider a wire of length L and
area of cross section A fixed at
one end to the rigid, then;
•Normal stress, 𝜎 =
𝐹
𝐴
•Longitudinal Strain =
𝑙
𝐿
.
𝑙
𝐿
𝐹

34. Y…
𝑌 =
𝐹
𝐴
𝑙
𝐿
=
𝐹𝐿
𝐴𝑙
• If r is the radius of the wire, then 𝐴 = 𝜋𝑟2
∴ 𝑌 =
𝐹𝐿
𝜋𝑟2 𝑙

36. Example 1
• A spring 60 cm long is
stretched by 2 cm by the
application of the load of
200g. What will be the
length when a load of
500 g is applied ?
• Solution
Y=
𝐹𝐿
𝐴𝑙
For the first case,
Y =
0.2 𝑥 9.8 𝑥 0.6
𝐴 𝑥 0.02
For the second case,
Y =
0.5 𝑥 9.8 𝑥 0.6
𝐴 𝑥 𝑙2
0.2 𝑥 9.8 𝑥 0.6
𝐴 𝑥 0.02
=
0.5 𝑥 9.8 𝑥 0.6
𝐴 𝑥 𝑙2
𝑙2 = 0.05 m = 5 cm
∴Total length = 60 + 5 = 65 cm

37. Example 2
• Four identical hollow cylindrical columns of steel
support a big structure of mass 50,000 Kg. the inner
and outer radii of each column are 30 cm and 40 cm
respectively. Assuming the load distribution to be
uniform, calculate the comprehension strain of each
column. The young’s modulus of steel is
2 𝑥 1011
𝑁𝑚−2

38. Solution
• 𝑅1 = 30 𝑐𝑚 = 0.3 𝑚,
• 𝑅2 = 40 𝑐𝑚 = 0.4 𝑚,
• Y = 2 𝑥 1011 𝑁𝑚−2
• m = 50,000 Kg,
• g = 9.8 𝑚𝑠−2
Cross-section area (𝑨);
𝐴 = 𝜋 𝑅2
2
− 𝑅1
2
𝐴 = 𝜋 0.42 − 0.32
𝐴 = 0.22 𝑚2
• The compressional force on each
column is;
𝐹 =
50,000 𝑥 9.8
4
= 1.225 𝑥 105
𝑁
• Compressional strain in each
column is:
𝑆𝑡𝑟𝑎𝑖𝑛 = 𝑆𝑡𝑟𝑒𝑠𝑠
𝑌 =
𝐹
𝐴
𝑌
=
1.225 𝑥 105 𝑁
0.22 𝑚2 𝑥 2 𝑥 1011 𝑁𝑚−2
∴ 𝑠𝑡𝑟𝑎𝑖𝑛 = 2.784 𝑥 10−6

39. Example 3
•Calculate the percentage increase in
length of a wire of diameter 2.2 mm
stretched by a load of 100 Kg.
Young’s modulus of wire is
12.5 𝑥 1010
𝑁𝑚−2
.

40. Solution
• 𝑌 = 12.5 𝑥 1010
𝑁𝑚−2
• 𝐹 = 100 𝐾𝑔 𝑥 9.8 𝑚𝑠−2
= 980 𝑁
• 𝐴 =
𝜋
4
𝑑2
=
𝜋
4
(2.2 𝑥 10−3
)2
= 3.8 𝑥 10−6 𝑚2
• 𝑌 =
𝐹𝐿
𝐴𝑙
• 𝑙
𝐿 =
𝐹
𝐴𝑌
=
980 𝑁
3.8 𝑥 10−6 𝑚2 𝑥12.5 𝑥 1010 𝑁𝑚−2
= 0.0021
∴ % increase in length = 𝑙
𝐿x 100
0.0021 𝑥 100
= 𝟎. 𝟐𝟏%

42. Bulk Modulus (K)
• This refers to situations in which the volume
(i.e. bulk) of a substance is changed by the
application of external normal stress.
Bulk modulus, 𝐾 =
𝑁𝑜𝑟𝑚𝑎𝑙 𝑆𝑡𝑟𝑎𝑖𝑛
𝑉𝑜𝑙𝑢𝑚𝑒𝑡𝑟𝑖𝑐 𝑠𝑡𝑟𝑎𝑖𝑛

43. Bulk Modulus…
• Normal stress, 𝜎 = 𝐹
𝐴
• Volumetric strain, 𝜀 𝑣𝑜𝑙 = − ∆𝑉
𝑉
• The negative sign is included to indicate that the
volume decreases with an increase in pressure.
• ∴ 𝐾 = −
𝐹
𝐴
∆𝑉
𝑉
= -
𝐹𝑉
𝐴∆𝑉
i.e. Pressure, p = 𝐹 𝐴
∴ 𝑌 = −𝑉
𝑝
∆𝑉

44. Example 4
• A spherical ball
contracts in volume by
0.01% when subjected
to a normal uniform
pressure of 108 𝑁𝑚2.
Find the bulk modulus
of the material.
Solution
𝐾 = 𝑉
𝑝
∆𝑉
𝑝 = 108
𝑁𝑚2
;
∆𝑉
𝑉 = 0.01% =
0.01
100
= 10−4
• K =
108
10−4
∴ 𝐾 = 1 𝑥 1012 𝑁𝑚2

46. Shear Modulus or Rigidity Modulus (𝜂)
• This refers to situations in which the shape of
a substance is changed by the application of
tangential stress.
𝜂 =
𝑇𝑎𝑛𝑔𝑒𝑛𝑡𝑎𝑙 𝑠𝑡𝑟𝑒𝑠𝑠
𝑆ℎ𝑒𝑎𝑟 𝑠𝑡𝑟𝑎𝑖𝑛

47. Shear Modulus…
• 𝑡𝑎𝑛𝑔𝑒𝑛𝑡𝑎𝑙 𝑠𝑡𝑟𝑒𝑠𝑠 =
𝐹
𝐴
• Shear strain = 𝜃 = tan𝜃
=
Δ𝑥
𝑙
∴ 𝜂 =
𝐹𝑙
𝐴∆𝑥

48. Example 5
• A rubber cube of side 20 cm has one side fixed
while a tangential force equal to the weight of
400 Kg is applied to the opposite face. Find (i)
shearing strain and (ii) the distance through
which the strained side moves. Given that
modulus of rigidity for rubber is 8 𝑥 106
𝑁𝑚2
.

49. Solution
• (i) shear stress =
𝐹
𝐴
=
400 𝑥 9.8
20 𝑥 10−2 2
= 9.8 𝑥 104 𝑁𝑚−2
𝜂 =
𝑆ℎ𝑒𝑎𝑟 𝑠𝑡𝑟𝑒𝑠𝑠
𝑆ℎ𝑒𝑎𝑟 𝑠𝑡𝑟𝑎𝑖𝑛
𝜃 =
𝑆ℎ𝑒𝑎𝑟 𝑠𝑡𝑟𝑒𝑠𝑠
𝜂
• 𝜃 =
9.8 𝑥 104 𝑁𝑚−2
8 𝑥 106 𝑁𝑚2
∴ 𝜃 = 0.0123
(ii) 𝜃 =
∆𝑥
𝐿
𝐿 = 𝜃 𝑥 𝐿
= 0.0123 x 0.2
= 0.0025 m
∴ 𝐿 = 0.25 cm

50. Strain Energy (U)

51. • When a body is subjected to gradual, sudden or impact load, the
body deforms and work is done upon it. If the elastic limit is not
exceed, this work is stored in the body. This work done or energy
stored in the body is called strain energy.
• Energy is stored in the body during deformation process and this
energy is called “Strain Energy”.
What is Strain Energy ?
Strain energy = Work done

52. Strain Energy…
• Work done (∆𝑊) is given by;
∆𝑊 = 𝐹∆𝑥
• Acceding to Hooke's law;
𝐹 = 𝑘𝑥
The total work done in increasing the extension
from 0 to x is given by;
𝑊 =
0
𝑥
𝑘𝑥𝑑𝑥
= 1
2 (𝑘𝑥2
)
∴ 𝑾 = 𝑼 = 𝟏
𝟐 𝑭𝒙

53. Strain Energy…
• The U equation can be expressed in another useful
form;
𝑈 =
1
2
𝑥
𝐹
𝐴
𝑥
𝑥
𝐿
𝑥 𝐿𝐴
U=
1
2
𝑥 𝑠𝑡𝑟𝑒𝑠𝑠 𝑥 𝑠𝑡𝑟𝑎𝑖𝑛 𝑥 𝑣𝑜𝑙𝑢𝑚𝑒
∴ 𝑆𝑡𝑟𝑎𝑖𝑛 𝑒𝑛𝑒𝑟𝑔𝑦 𝑝𝑒𝑟 𝑢𝑛𝑖𝑡 𝑣𝑜𝑙𝑢𝑚𝑒 𝑖𝑠;
U=
1
2
𝑥 𝑠𝑡𝑟𝑒𝑠𝑠 𝑥 𝑠𝑡𝑟𝑎𝑖𝑛

54. Example 6
• Calculate the increase in energy of a brass bar
of length 0.2 m and cross-sectional area 1 𝑐𝑚2
when compressed with a force of 49 N along
its length. Young’s modulus of brass =
1.0 𝑥 1011
𝑁𝑚−2
.

55. Solution
L = 1.0 𝑥 1011 𝑁𝑚−2
A =1 𝑐𝑚2 = 1 𝑥10−4 𝑚
𝑌 =
𝐹𝐿
𝐴𝑥
𝑜𝑟 𝑥 =
𝐹𝐿
𝐴𝑌
𝑈 =
1
2
𝑥 𝐹 𝑥
𝐹𝐿
𝐴𝑌
∴ 𝑈 =
𝐹2
𝐿
2𝐴𝑌
• 𝑈 =
(49)2 𝑥 0.2
2 𝑥 1.0 𝑥 10−4 𝑥 (1.0 𝑥1011)
U= 2.4 𝑥 10−5 𝐽

56. • When body subjected to axial tensile force, it elongates
and contracts laterally
• Similarly, it will contract and its sides expand laterally
when subjected to an axial compressive force
POISSON’S RATIO

57. • Strains of the bar are:
POISSON’S RATIO…
long =
δ
L
lat =
δ’
r
Poisson’s ratio, ν = −
lat
long
• Early 1800s, S.D. Poisson realized that within elastic
range, ration of the two strains is a constant value,
since both are proportional.

58. • ν is unique for homogenous and isotropic material
• Why negative sign? Longitudinal elongation cause
lateral contraction (-ve strain) and vice versa
• Lateral strain is the same in all lateral (radial) directions
• Poisson’s ratio is dimensionless, 0 ≤ ν ≤ 0.5
3.6 POISSON’S RATIO…

59. THANK YOU