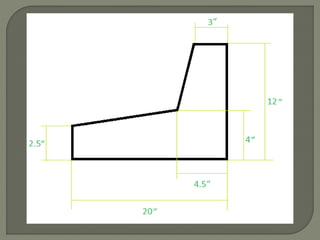
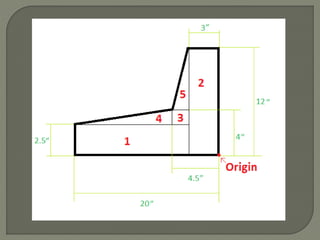
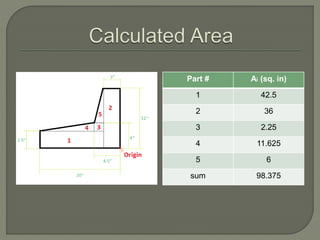
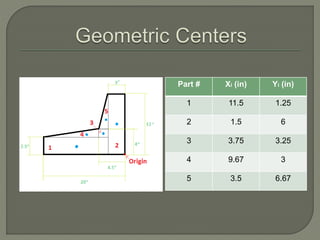
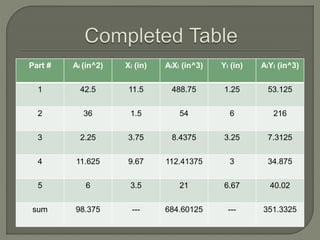
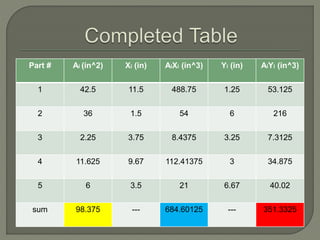
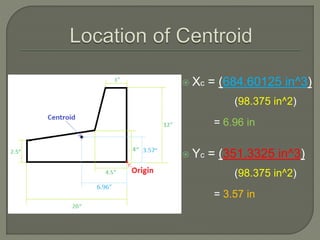
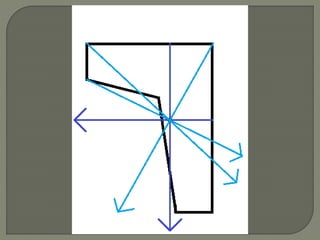
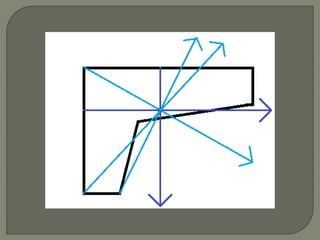
The document provides steps to calculate the geometric center of an irregular shape: 1. Divide the shape into components with easily calculable areas and add the areas. 2. Find the geometric center and distance to the origin for each component. 3. Use the calculated areas and distances to determine the overall geometric center of the shape using formulas that sum the weighted distances.

1. By Dillon O’Connor

3. Divide the shape into components that can
have their area easily calculated.
Add these areas together for the area of
the shape.

5. Part # Ai (sq. in)
1 42.5
2 36
3 2.25
4 11.625
5 6
sum 98.375

6. Find the geometric center of each
component that you have divided the
shape into.
Calculate the distance from the origin to
the geometric center on an axis.
Remain consistent with the shapes used
from calculating the area.

7. For rectangles:
• Half the length of the rectangle’s side along an
axis
For right triangles:
• 1/3 of the distance from the triangle’s vertex that is
a right angle along an axis.
Remember to add the distance between
the origin and the start of the shape.

8. Part # Xi (in) Yi (in)
1 11.5 1.25
2 1.5 6
3 3.75 3.25
4 9.67 3
5 3.5 6.67

9. Part # Ai (in^2) Xi (in) AiXi (in^3) Yi (in) AiYi (in^3)
1 42.5 11.5 488.75 1.25 53.125
2 36 1.5 54 6 216
3 2.25 3.75 8.4375 3.25 7.3125
4 11.625 9.67 112.41375 3 34.875
5 6 3.5 21 6.67 40.02
sum 98.375 --- 684.60125 --- 351.3325

10. For the distance from the origin along the
y-axis:
• Yc = The sum of the AiYi (in^3)
The sum of the Ai (in^2)
For the distance from the origin along the
x-axis:
• Xc = The sum of the AiXi (in^3)
The sum of the Ai (in^2)

11. Part # Ai (in^2) Xi (in) AiXi (in^3) Yi (in) AiYi (in^3)
1 42.5 11.5 488.75 1.25 53.125
2 36 1.5 54 6 216
3 2.25 3.75 8.4375 3.25 7.3125
4 11.625 9.67 112.41375 3 34.875
5 6 3.5 21 6.67 40.02
sum 98.375 --- 684.60125 --- 351.3325

12.  Xc = (684.60125 in^3)
(98.375 in^2)
= 6.96 in
 Yc = (351.3325 in^3)
(98.375 in^2)
= 3.57 in