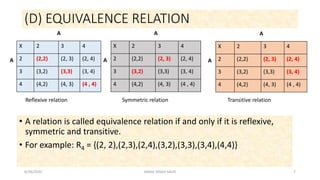
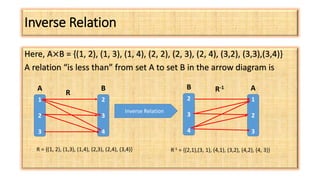
The document discusses different types of relations, including reflexive, symmetric, transitive, and equivalence relations. It provides examples of each type of relation and defines their key properties. Inverse relations are also discussed, where the ordered pairs of a relation R are reversed to form the inverse relation R-1. An example demonstrates finding the domain, range, and inverse of a given relation defined by an equation.

1. TYPES OF A RELATION

2. Types of a relation
• Reflexive Relation
• Symmetric Relation
• Transitive Relation
• Equivalence Relation
6/28/2020 JANAK SINGH SAUD 2

3. Types of a relation
• Let us consider A = {2, 3, 4}
• Then the Cartesian product
A X A = {(2,2),(2,3),(2,4),(3,2),(3,3),(3,4),(4,2),(4,3),(4,4)}
A
A
X 2 3 4
2 (2,2) (2, 3) (2, 4)
3 (3,2) (3,3) (3, 4)
4 (4,2) (4, 3) (4 , 4)
6/28/2020 JANAK SINGH SAUD 3

4. (A) REFLEXIVE RELATION
• A relation R is called reflexive if every element of the relation is
related to itself.
• It is denoted by xRx
• For example: R1= {(2, 2), (3 ,3),(4, 4)
A
A
X 2 3 4
2 (2,2) (2, 3) (2, 4)
3 (3,2) (3,3) (3, 4)
4 (4,2) (4, 3) (4 , 4)
6/28/2020 JANAK SINGH SAUD 4

5. (B) SYMMETIC RELATION
• In a relation, if the first and second components of the ordered pairs are
interchanged, the relation still holds. It is called symmetric relation.
• It is written as is xRy then yRx.
• If x = y then the relation is Anti-symmetric.
• For example R2= {(2, 3), (3, 2)
R3 = {(2,3),(3,2),(2,4),(4,2)}
A
A
X 2 3 4
2 (2,2) (2, 3) (2, 4)
3 (3,2) (3,3) (3, 4)
4 (4,2) (4, 3) (4 , 4)
6/28/2020 JANAK SINGH SAUD 5

6. ( C) TRANSITIVE RELATION
• A relation is called transitive if aRb and bRc gives aRc. Then a is
related to b and b is related to c the a is related to c.
• For example: {(2, 3), (3, 4), (2, 4)}
A
A
X 2 3 4
2 (2,2) (2, 3) (2, 4)
3 (3,2) (3,3) (3, 4)
4 (4,2) (4, 3) (4 , 4)
6/28/2020 JANAK SINGH SAUD 6

7. (D) EQUIVALENCE RELATION
• A relation is called equivalence relation if and only if it is reflexive,
symmetric and transitive.
• For example: R4 = {(2, 2),(2,3),(2,4),(3,2),(3,3),(3,4),(4,4)}
A
A
X 2 3 4
2 (2,2) (2, 3) (2, 4)
3 (3,2) (3,3) (3, 4)
4 (4,2) (4, 3) (4 , 4)
A
A
X 2 3 4
2 (2,2) (2, 3) (2, 4)
3 (3,2) (3,3) (3, 4)
4 (4,2) (4, 3) (4 , 4)
A
A
X 2 3 4
2 (2,2) (2, 3) (2, 4)
3 (3,2) (3,3) (3, 4)
4 (4,2) (4, 3) (4 , 4)
Reflexive relation Symmetric relation Transitive relation
6/28/2020 JANAK SINGH SAUD 7

8. Inverse Relation
Here, A×B = {(1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4), (3,2), (3,3),(3,4)}
A relation “is less than” from set A to set B in the arrow diagram is
1
2
3
A
2
3
4
B
R
2
3
4
B
1
2
3
A
Inverse Relation
R-1
R = {(1, 2), (1,3), (1,4), (2,3), (2,4), (3,4)} R-1 = {(2,1),(3, 1), (4,1), (3,2), (4,2), (4, 3)}

9. Inverse Relation
1
2
3
A
2
3
4
B
R
2
3
4
B
1
2
3
A
Inverse Relation
R-1
R = {(1, 2), (1,3), (1,4), (2,3), (2,4), (3,4)} R-1 = {(2,1),(3, 1), (4,1), (3,2), (4,2), (4, 3)}
R = “is less than” relation R-1 = “is greater than” relation
Symbolically: If R = {(x, y): x∈A, y ∈B}, then R-1 = {(y, x): y ∈ B and x∈A}

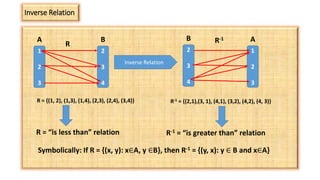
10. A relation is defined by R = {(x, y): 1< x < 4; y = 2x – 1}. Find the domain and range
of the function . Also find the inverse relation
• Domain x ∈ {2, 3}
• Range: when x = 2, y = 2x 2 – 1 = 3
• when x = 3, y = 2 x 3 – 1 = 5
• ∴Range = {3, 5]
• So, relation R = {(2, 3), (3, 5)}
Hence, Inverse relation R-1{(3, 2), (5, 3)}

11. https://www.youtube.com/channel/UCGxSYD_UZLzXfmAzxaRyYhw?vie
w_as=subscriber
https://www.facebook.com/janaksinghsaud
https://www.slideshare.net/janaksinghsaud
saudjanaksingh@gmail.com
6/28/2020 JANAK SINGH SAUD 11