1) Set theory helps organize things into groups and understand logic. Key contributors include Georg Cantor, John Venn, George Boole, and Augustus DeMorgan.
2) A set is a collection of elements. A subset contains only elements that are also in another set. The cardinality of a set refers to the number of elements it contains.
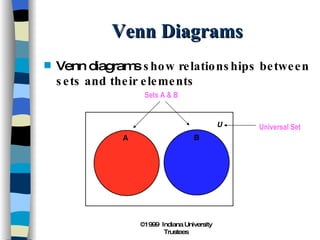
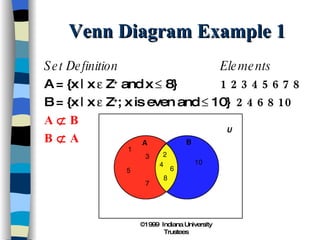
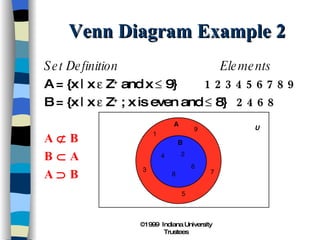
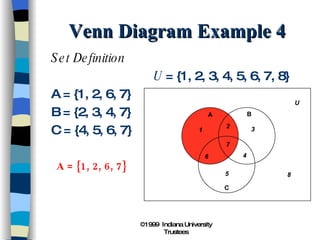
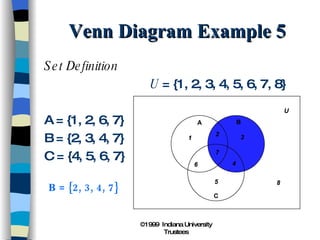
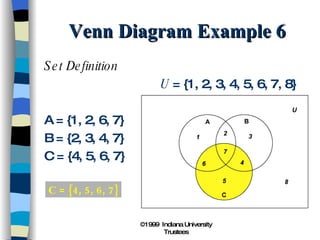
3) Venn diagrams show relationships between sets using overlapping circles to represent their common elements.