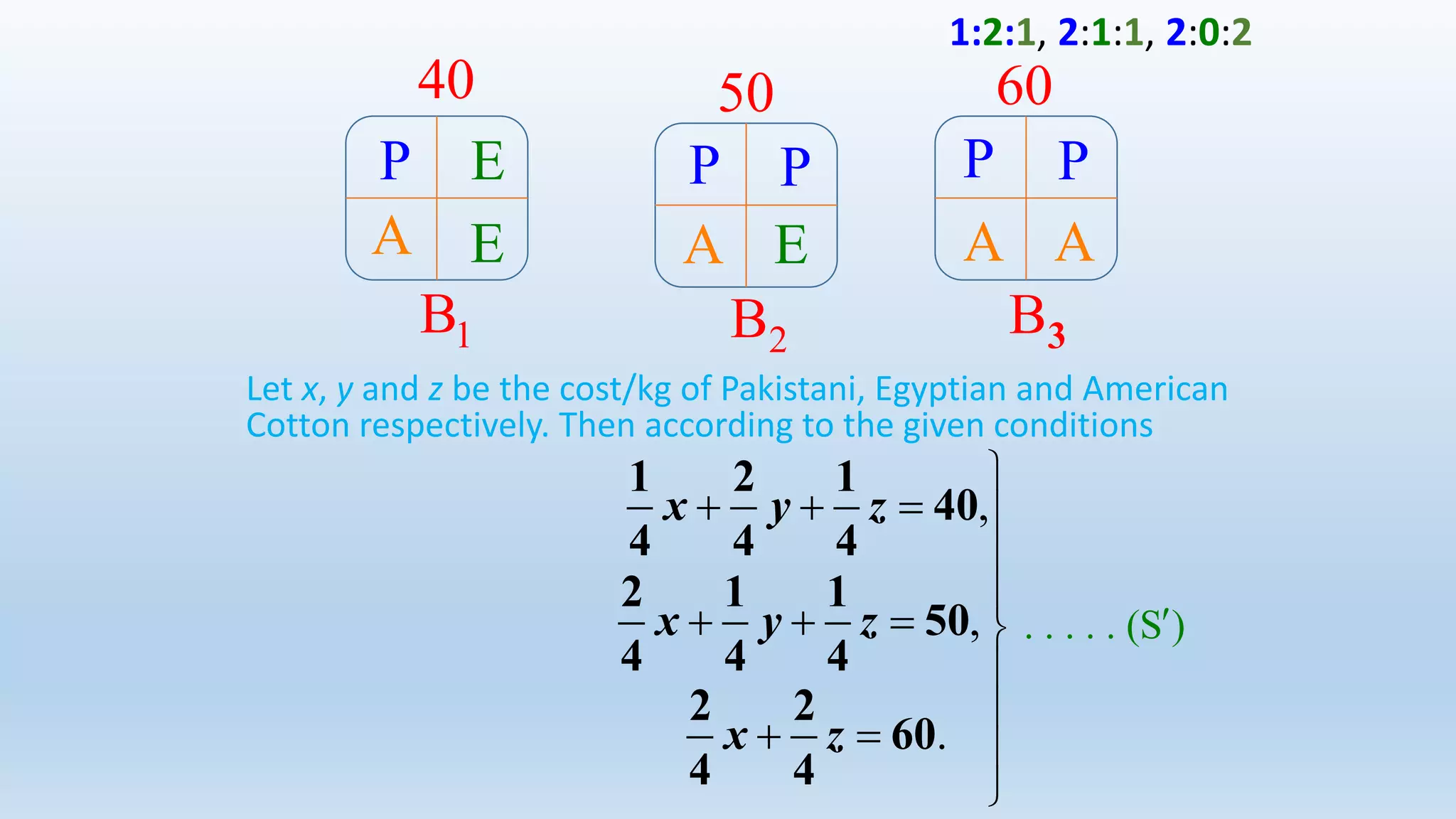
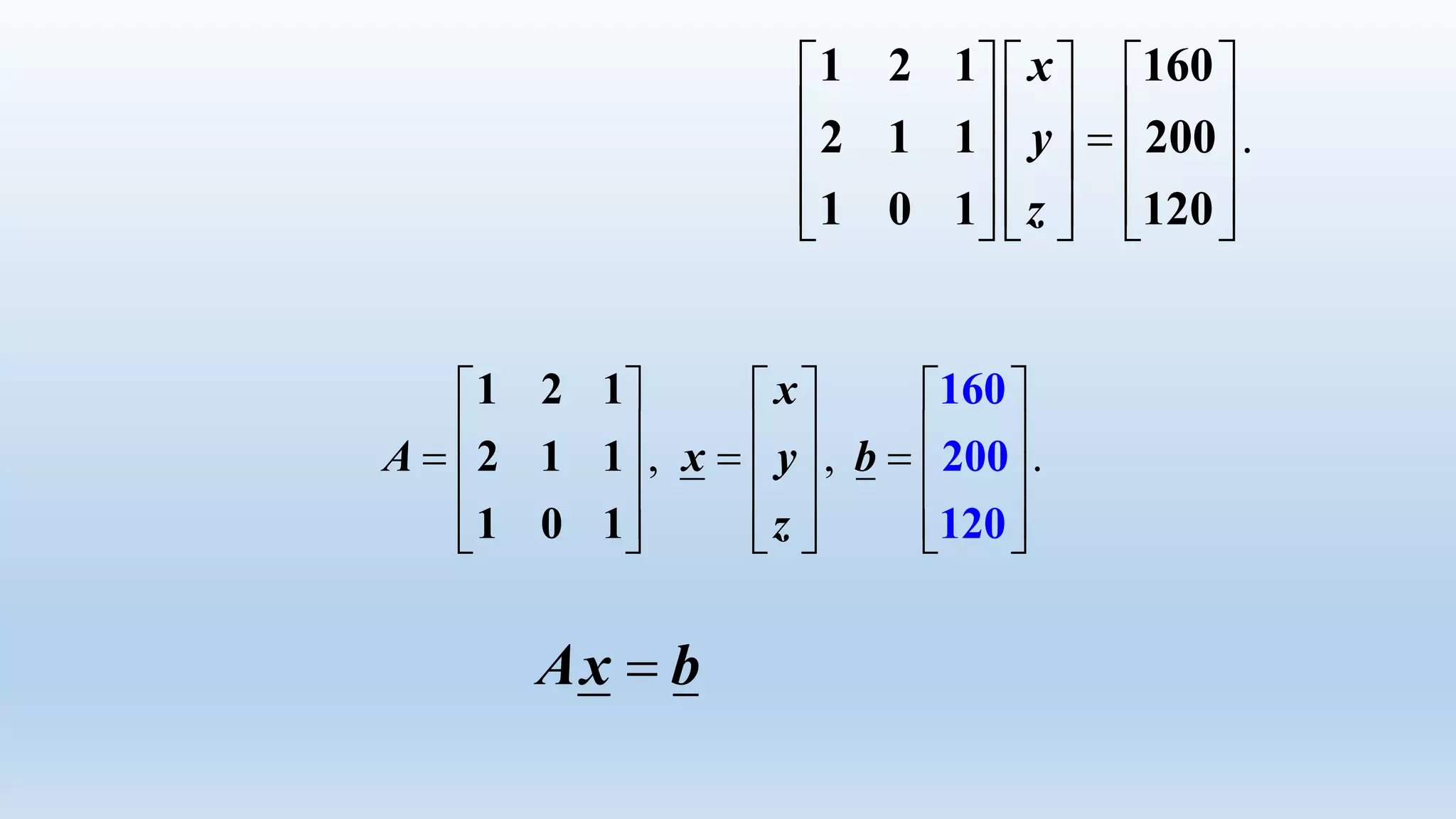
The document discusses Cramer's rule and provides two examples of its application. Cramer's rule is a method to solve systems of linear equations. It expresses the solution in terms of determinants of the coefficient matrix and matrices obtained by replacing columns with the constants on the right side of the equations. The first example uses Cramer's rule to find the cost per scoop of three ice cream flavors given their total costs and ingredient ratios. The second example determines the cost per kg of cotton from three countries used in blends for different yarn brands.

2. Groups members
Name(Roll No.)
 Mubashir(13)
 Muhammad nouman(19)
 Rai Amad ud din(27)
Presentation topic: Cramer Rule’s and its Application

3. What is Cramer rule and it formula
Cramer rule is the mathematical technique to solve the systems of
Linear equations.
In linear algebra, Cramer's rule is an explicit formula for the solution of a
system of linear equations with as many equations as unknowns, valid
whenever the system has a unique solution. It expresses the solution in
terms of the determinants of the (square) coefficient matrix and of
matrices obtained from it by replacing one column by the column vector
of right-hand-sides of the equations.
formula Ax=b

4. Applications with Example

5. A B C
37 39 44
?
Example no.1

6. . . . . . (S)





.
     
          
          
2 3 2 37
3 2 2 39
5 1 1 44
x
y
z
Let x, y and z be the cost/scoop of Pineapple, Strawberry and Vanilla
flavors, respectively. Then according to the given conditions
In matrix form, we can write it as:
.x y z  5 1 1 44
,x y z  2 3 2 37
,3 2 2 39x y z  

7. .
     
          
          
2 3 2 37
3 2 2 39
5 1 1 44
x
y
z
, , .
x
A x y b
z
     
            
          
2 3 2
3 2 2
5 1 1
37
39
44
Ax b

8. 2 3 2 37
3 2 2 , , 39 .
5 1 1 44
x
A x y b
z
     
            
          
1
3 2
2 2 ,
1
37
39
44 1
A
 
   
  
2
37
39
44
2 2
3 2 ,
5 1
A
 
   
  
3
2 3
3 2
5 1
37
39
44
A
 
   
  
2 3 2
3 2 2
5 1 1
A
 
   
  

9. , 7A
2 3 2 37
3 2 2 , , 39 .
5 1 1 44
x
A x y b
z
     
            
          
= 2(2x1-1x2) -3(3x1-5x2) +2(3x1-5x2)
,A 1 49 = 37(2x1-1x2) -3(39x1-44x2) +2(39x1-44x2)
A
2 3 2
3 2 2
5 1 1

A1
37
3
3 2
2 29
144 1

,A 2 35 A2
2 2
3 2
37
39
5 144
 = 2(39x1-44x2) -37(3x1-5x2) +2(3x1-5x39)
,3 28A  A3
2 3
3
37
392
45 1 4
 = 2(2x44-1x39) -3(3x44-5x39) +37(3x44-5x2)
One pineapple(x)=7 Rs. One Stawbarry(y)=5Rs. One Vinilla(z)=4Rs.

10.  A textile industry sells
3 brands: B1, B2 and B3 of yarn,
each of which is a blend of
Pakistani, Egyptian and American
cotton in ratios:
1:2:1, 2:1:1 and 2:0:2.
If cost/kg of B1, B2 and B3 is Rs. 40, 50
and 60 respectively,
Example no.2
find the cost/kg of cotton of each country.

11. 1B 2B B3
P
EA
1:2:1, 2:1:1, 2:0:2
E P P P P
A AEA
40 50 60
Let x, y and z be the cost/kg of Pakistani, Egyptian and American
Cotton respectively. Then according to the given conditions
. . . . . (S )










,x y z  
1 2 1
40
4 4 4
,x y z  
2 1 1
50
4 4 4
.x z 
2 2
60
4 4

12. . . . . . (S,
.
)
,x y z
x y z
x z
   

   
  
1 2 1 160
2 1 1 200
1 1 120
. . . . . (
,
,
.
S )
x y z
x y z
x z

   


   




 

1 2 1
40
4 4 4
2 1 1
50
4 4 4
2 2
60
4 4
.
x
y
z
     
          
          
1 2 1 160
2 1 1 200
1 0 1 120
In matrix form, we can write it as:

13. , , .
x
A x y b
z
     
            
          
160
2
1 2 1
2 1 1 00
11 00 1 2
Ax b
.
x
y
z
     
          
          
1 2 1 160
2 1 1 200
1 0 1 120

14. x
A x y b
z
1 2 1 160
2 1 1 , , 200 .
1 0 1 120
     
            
          
A1
160
200
12
2 1
1 1 ,
0 0 1
 
   
  
A2
160
200
1
1 1
2 1 ,
1 20 1
 
   
  
A3
1 2
2 1
1 0
160
200
120
 
   
  
A
1 2 1
2 1 1
1 0 1
 
   
  

15. ,A  2
,A  1 120
A
1 2 1
2 1 1
1 0 1

A1
160
20
2 1
1 10
1120 0

,A  2 40 A2
160
2
1 1
2 100
1 1120

,A  3 120 A3
1 2
2 1
160
200
01 0 12

x
A x y b
z
1 2 1 160
2 1 1 , , 200 .
1 0 1 120
     
            
          
= 1(1x1-0x1) -2(2x1-1x1) +1(2x1-1x1)
= 160(1x1-0x1) -2(200x1-120x1) +1(200x1-120x1)
= 1(200x1-120x1) -160(2x1-1x1) +1(2x1-1x200)
= 1(1x120-0x200) -2(2x120-1x200) +160(2x120-1x1)

16. x y z ( , , ) ( , ,2060 60).











,A  2
, ,A A A     1 3 3120 40 120
According to
Cramer’s Rule
.z
A
A 
  

3 120
60
2
,y
A
A 
  

2 40
20
2
,x
A
A 
  

1 120
60
2
x
A x y b
z
1 2 1 160
2 1 1 , , 200 .
1 0 1 120
     
            
          