1. The document is the question paper for a mathematics exam with 15 multi-part questions testing a variety of skills including algebra, geometry, trigonometry, and calculus.
2. The first page provides formulae that may be useful for solving problems on the exam. These include formulas for circles, vectors, trigonometric identities, derivatives, and integrals.
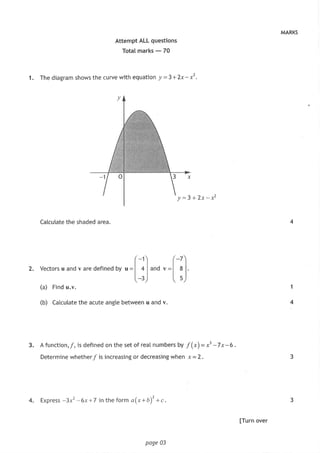
3. The questions cover topics like finding equations of lines and circles, solving equations, sketching graphs, vector and trigonometric calculations, and evaluating limits and derivatives. Working step-by-step through each question is required to earn full credit.






![Page 07
MARKS
14. (a) Evaluate log5 25.
(b) Hence solve ( )4 4 5log log 6 log 25x x+ − = , where 6>x .
15. The diagram below shows the graph with equation ( )=y f x , where
( ) ( )( )2
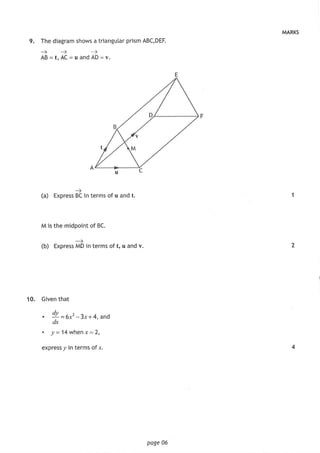
= − −f x k x a x b .
y
(1, 9)
−5 O 4
x
(a) Find the values of a, b and k.
(b) For the function ( ) ( )= −g x f x d , where d is positive, determine the range of
values of d for which ( )g x has exactly one real root.
[END OF QUESTION PAPER]
1
5
3
1](https://image.slidesharecdn.com/h2016-2018-190501110305/85/H-2016-2018-7-320.jpg)
![Page 08
[BLANK PAGE]
do not write on this page](https://image.slidesharecdn.com/h2016-2018-190501110305/85/H-2016-2018-8-320.jpg)

























![Page 08
MARKS
10. (a) Given that ( )
1
2 27y x= + , find
dy
dx
.
(b) Hence find
2
4
7
x
dx
x +
⌠
⎮
⌡
.
11. (a) Show that sin 2x tan x = 1 − cos 2x, where
3
2 2
x
π π
< < .
(b) Given that ( ) sin 2 tanf x x x= , find ( )f x′ .
[END OF QUESTION PAPER]
2
1
4
2](https://image.slidesharecdn.com/h2016-2018-190501110305/85/H-2016-2018-36-320.jpg)