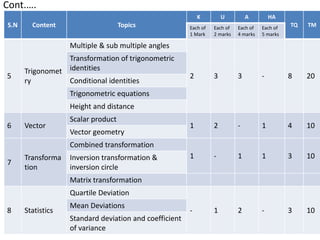
This document provides an overview of teaching optional mathematics. It discusses the nature and purpose of optional mathematics, including developing additional knowledge and skills beyond compulsory mathematics. It outlines general objectives like introducing functions and graphs. Techniques like demonstration, problem-solving, and cooperative learning are described. Materials include textbooks, practice books, and GeoGebra. Students will be evaluated through methods like observation, participation, practicums, tests, and formative/summative assessments.

1. WINTER
Template
Curriculum Sharing
of
Optional
Mathematics
Presented by: JANAK SINGH SAUD
♥

2. Mathematics as a
necessity of
civilization

3. Nature of
Mathematics
Why to teach
Mathematics
Steps of
learning
Optional
mathematics
as a Optional
subject. Why?
Purpose of
Optional
mathematics
General
objectives of
Optional
Mathematics
Techniques
and strategies
of
Mathematics
Teaching
learning
materials
Evaluation
process
Purpose of
Evaluation
Record
keeping
Framework
of
this session

4. ❑Mathematics is a language
❑Mathematics is way of thinking
❑Mathematics is pattern of science
❑Mathematics is organized structure of
knowledge
❑Mathematics is practical science
❑Inductive nature of mathematics
❑Mathematics is both science and art
❑Telescopic and microscopic nature of
mathematics

5. • Arithmetical skills which are needed for use at
home or office or workplace.
• Basis of scientific development and modern
technology
• Use of mathematical technique as
management tool in commerce and industries
• Fundamental to study of physical science and
engineering of all kind.
• For enjoyment for example, puzzles corners
which help to solve them.

6. Mathematics in real Practice
Type of cake Flour Fat Profit
A 250 gm 40 gm Rs. 5
B 100 gm 50 gm Rs. 10
Total 5000 gm 2000 gm
Let, x an y be the no. of cakes A and B.
Total quantity of flour = 250x + 100 y
Total quantity of fat = 40 x + 50 y
And the total profit = 5x + 10 y = Objective function
Thus he has to produce 40 pieces of cake B and no cake A
to get maximum profit of Rs. 400
Maximum value is 400

7. There are certain steps or methods that should
be applied in learning process which are all
follows:

8. Steps of learning

9. • Along with the knowledge and skills of
different subjects and areas, students must
be equipped with knowledge and skills of
mathematical concepts for their overall
development.

10. engineering, medical science, and pure science

11. Purpose
• To develop additional knowledge and skills in most
of the concepts which are included in compulsory
mathematics.
• To provide wider knowledge on algebra (excluding
the concepts which are already mentioned in
compulsory mathematics), matrix, coordinate
geometry, trigonometry, vector, transformation,
and statistics and so on.

12. • The curriculum of an optional mathematics is
designed by collecting suggestions from
subject teachers and experts to make it useful,
effective, standard and practical.

13. 1. To introduce of relation and function and explain its characteristics
2. To draw the graph of function
3. To define the inverse and composite functions
4. To find the positive, negative base of exponential expression, to find product and
division and to solve relates equations.
5. To introduce with the polynomial and apply the remainder and factor theorem .
6. To understand the definition of Series, A.S and G.S and solve the their problem.
7. To find the A.M., G.M and relation between them
8. To find the sum of natural numbers of A.S and G.S
9. To maximize and minimize the feasible region bounded by the polygon of given
inequalities.
10. To solve the linear and quadratic equations, draw their graph and quadratic
equation by graphical way.
11. To define , present the matrix and its operations.
12. To solve the simultaneous equations by matrix method.
13. To find the trigonometric ratios of compound angles and solve the problem
related to these compound angles.
14. To prove the conational trigonometric identities
15. To solve the trigonometric equations
16. To solve the problems of height and distance involving two angles elevation and
depression.

14. Specification Grid of Opt. Maths
S.
N
Content Topics
K U A HA
TQ TM
Each of
1 Mark
Each of
2 marks
Each of
4 marks
Each of
5 marks
1 Algebra
Function
2 3 2 1 8 21
Polynomial
Sequence & Series
Linear programming
Quadratic equation and graph
2
Limit and
continuity
Continuity and discontinuity
1 - 1 - 2 5
3 Matrix
Determinant and inverse of matrix
1 2 1 - 4 9
Solve equation by matrix method
Cramer’s rule
4
Coordinate
geometry
Angle between two lines
2 2 1 1 6 15
Pair of straight lines
Conic sections
Circle

15. Cont.….
S.N Content Topics
K U A HA
TQ TM
Each of
1 Mark
Each of
2 marks
Each of
4 marks
Each of
5 marks
5
Trigonomet
ry
Multiple & sub multiple angles
2 3 3 - 8 20
Transformation of trigonometric
identities
Conditional identities
Trigonometric equations
Height and distance
6 Vector
Scalar product
1 2 - 1 4 10
Vector geometry
7
Transforma
tion
Combined transformation
1 - 1 1 3 10
Inversion transformation &
inversion circle
Matrix transformation
8 Statistics
Quartile Deviation
- 1 2 - 3 10
Mean Deviations
Standard deviation and coefficient
of variance

17. WINTER
Template
Techniques and
Strategies in
Teaching
Mathematics

18. WINTER
Template
➢Questioner and Discussion
Approach
➢Experimental Approach
➢Inductive and deductive Approach
➢Discovery Approach
➢Synthetic and analytical Approach
➢Problem Solving Approach
➢Demonstration approach

19. DEMONSTRATION
APPROACH

21. PROBLEM
SOLVING

22. PROBLEM-SOLVING
• a learner-directed strategy in which
learners “think patiently and analytically
about complex situations in order to find
answers to questions”.

24. COOPERATIVE
Learning

25. COOPERATIVE LEARNING
•eliminates competition among learners. It
encourages them to work together towards
common goals.
•It fosters positive intergroup attitudes in
the classroom. It encourages learners to
work in small groups to learn.

27. Discovery
Approach

28. A. DISCOVERY APPROACH
The ultimate goal of this approach
is that learners learn how to learn
rather than what to learn.
•for developing their higher-order
thinking skills.

29. BRAIN
STORMING

30. BRAINSTORMING
• It is an excellent strategy
for stimulating
creativity among
learners.

31. Materials
– Power Point presentations (visual aids)
– Text Books
– Practice Book
– Question Bank
– Multimedia materials: Instructional video or audio
– Geo Gebra (GeoGebra is a cross-platform Dynamic
Mathematics Software that integrates Geometry and
Algebra)
– www.slideshare.net
(https://www.slideshare.net/search/slideshow?search
from=header&q=janak+singh+saud)

32. For Absent Students

33. Power point presentation

34. Geo Gebra

35. Evaluation process/scheme
To examine if students are able to achieve
expected objective or not.
To inspect if students are ready with the prerequisites to
learn new lesson of mathematics or not.
To provide feedback on accomplishment (what
and how much have the students learnt)
To provide feedback on effectiveness of teaching
to the teachers ( what and how much has been
taught)
To determine a level of the students by evaluating
their outcome.
The evaluation process of an optional mathematics
should be targeted to achieve the following objectives.

36. While teaching mathematics, students
will be evaluated by using following
methods:
• Observation
• Students’ participation ( by involving students
in different activities and letting them to apply
in their daily life)
• Practicum
• Written/class test, homework

37. Written
tests
Formative
assessment
The test
administered in
different times
monthly,
weekly,
at the end of a
lesson,
quarterly,
twice a year
Summative
Assessment

41. www.slideshare.net