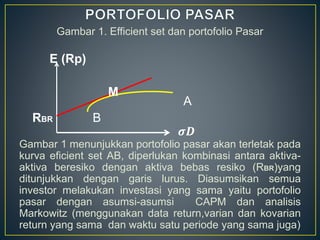
Dokumen ini membahas teori portofolio dan analisis investasi berdasarkan model CAPM yang dikembangkan oleh Sharpe, Lintner, dan Mossin. Asumsi-asumsi utama dalam model ini termasuk likuiditas, tidak ada biaya transaksi, dan ekuilibrium pasar, yang berimplikasi bahwa semua investor akan memilih portofolio pasar sebagai portofolio optimal. Contoh soal yang diberikan menunjukkan perhitungan return ekspektasian dan analisis nilai dari beberapa saham menggunakan CAPM.

1. TITIK INAYATI
Daftar Pustaka : Teori Portofolio dan Analisis
Investasi, Prof. Dr. Jogiyanto Hartono, MBA.,Ak
(2000)

2. •Bentuk standar CAPM
pertama kali dikembangkan
secara terpisah oleh Sharpe
(1964), Lintner (1965) dan
Mossin (1969), sehingga
model ini disebut dengan
CAPM bentuk Sharpe-
Lintner-Mossin.

3. • Semua investor mempunyai waktu satu periode
yang sama,
• Semua investor mengambil keputusan investasi
berdasarkan pertimbangan nilai return
ekspektasian dan deviasi standart return dari
portofolionya.
• Skema investor mempunyai harapan yang
seragam terhadap faktor-faktor input yang
digunakan dalam mengambil keputusan
portofolio.
• Semua investor saling meminjamkan atau
meminjam sejumlah dana dengan jumlah yang
tidak terbatas pada tingkat suku bunga bebas

4. • Semua aktiva dapat dipecah-pecah menjadi
bagian yang lebih kecil dengan tidak terbatas,
• Semua aktiva dapat dipasarkan secara likuid
sempurna.
• Tidak ada biaya transaksi
• Tidak terjadi Inflasi
• Tidak ada pajak pendapatan pribadi
• Investor sebagai penerima harga
• Pasar modal dalam kondisi ekulibrium.

5. • Ekuilibrium pasar terjadi jika harga-harga
aktiva berada di tingkat yang tidak dapat
memberikan insentif untuk melakukan
perdagangan spekulatif ( Jones,1995).
• Impilkasinya :
• 1. Semua investor akan memilih portofolio
pasar
• 2. Portofolio pasar ini merupakan portofolio
aktiva yang berisiko optimal.

6. Gambar 1. Efficient set dan portofolio Pasar
Gambar 1 menunjukkan portofolio pasar akan terletak pada
kurva eficient set AB, diperlukan kombinasi antara aktiva-
aktiva beresiko dengan aktiva bebas resiko (RBR)yang
ditunjukkan dengan garis lurus. Diasumsikan semua
investor melakukan investasi yang sama yaitu portofolio
pasar dengan asumsi-asumsi CAPM dan analisis
Markowitz (menggunakan data return,varian dan kovarian
return yang sama dan waktu satu periode yang sama juga)
A
M
B
E (Rp)
RBR
𝝈𝑫

7. Gambar 2. Garis Pasar Modal
Q
Garis Pasar Modal (GPM)
Gambar 2 menunjukkan semua kemungkinan kombinasi
portofolio effisien yang terdiri dari aktiva-aktiva berisiko dan
aktiva bebas resiko. Jika portofolio pasar berisi aktivatidak
beresiko maka resiko akan sama dengan nol (𝝈𝑷=0 ) dan return
ekspektasian sebesar E(RM), sehingga E(RM) > E(RBR) atau
aktiva tidak beresiko. Selsisih Return E(RM) – E(RB) = 𝝈𝑴
disebut premium portofolio pasar.
Premium Resiko = E (RM) -
RBR
M
Resiko Portofolio Pasar
E (Rp)
RBR
𝝈𝑷
𝝈𝑴
E(RM)

8. • Rumus Harga Pasar dari resiko =
𝑬 𝑹𝑴 −𝑹𝑩𝑹
𝝈𝑴
Contoh Soal 1 :
Return ekspektasion portofolio pasar (E(RM)) adalah 20 %
dengan standart deviasi 𝜎𝑀 Sebesar 5 % Return Aktiva bebas
resiko (RBR) sebesar 12 % besarnya slope GPM sbb:
Slope GPM =
20% −12 %
5 %
= 1,6
Contoh Soal 2 :
Slope GPM = 1,6 dengan standart deviasi 𝜎𝑀
Sebesar 5 % maka tambahan return ekspektasion portofolio
sbb:
Rumus tambahan ekspektasion portofolio Pasar = Slope
GPM . 𝝈𝑴
Maka :
Tambh Ekspektasion portofolio Pasar = 1,6 . 5 % = 8 %

9. • Contoh Soal 3 :
• Standart deviasi 𝜎𝑀 Sebesar 10 % Return
Aktiva bebas resiko (RBR) sebesar 12 %
besrnya slope GPM 1,6, besarnya return
ekspektasion sbb:
• Rumus Return ekspektasion = Return
aktiva Bebas E (RP) + Harga dari resiko
(RBR) X Besarnya resiko (𝜎𝑃)
Maka Return Ekspektasian =
12 % + 1,6 . 10 % = 28 %

10. • Garis pasar modal mengambarkan tradeoff antara resiko
dan return ekspektasion untuk portofolio efisien, etapi
bukan untuk sekuritas individual.Garis lain yang
menunjukkan tredeoff antara resiko dan return
ekspektasion untuk sekuritas individual disebut dengan
garis pasar sekuritas (GPS) atau security Market Lini
(SML) GPS merupakan pengambaran secara grafis dari
model CAPM.
• Tambahan return ekspektasion terjadi karena diakibatkan
oleh tambahan resiko dari portofolio bersangkutan.
Tambahan return ekspektasion oleh tambahan resiko
sekuritas individual diukur dengan Beta. Beta untuk
portofolio pasar bernilai 1, Suatu sekuritas yang
mempunyai Beta lebih kecil dari 1dikatakan beresiko
lebih kecil dari resiko portofolio pasar.

11. Gambar 3. Garis Pasar Sekuritas
Q
Garis Pasar Sekuritas (GPS)
Gambar 3 menunjukkan titik M sebagai portofolio pasar dengan
Beta senilai 1 dengan return ekspektasion sebesar E(RM) untuk
aktiva yang tidak mempunyai resiko sistimatik. Beta untuk aktiva
yang bebas resiko mempunyai return ekspektasian sebesar
RBR yanng merupakan intercept GPS, dengan asumsi GPS
adalah garis linier.
M
E (Rp)
RBR
𝑩𝒆𝒕𝒂
𝟏, 𝟎
E(RM)

12. • Contoh Soal 4 :
• Return portofolio pasar Sebesar 15 %
Return Aktiva bebas resiko (RBR) sebesar
12 % Beta saham A = 1,8 maka besarnya
return ekspektasion sbb:
• Rumus nya sbb:
• E (Ri)= RBR +βi . {E(RM) – RBR}
• E (RA) = 12 % + 1,8 .(15% - 12 % )
• = 12 % + 5,4 %
= 17,4 %

13. • Contoh Soal 5
• Diketahu IHSGt sekarang = 2.400
• IHSGt-1periode lalu = 2.000
• Suku bunga SBI = 8 % Data 3 saham sbb:
• Return pasar :
• RM = (IHSGt – IHSGt-1) / IHSGt-1
= 2.400 – 2.000 / 2000 = 20 %
Keterangan Saham A Sham B Saham C
Harga Periode sekarang
(Pt)
Rp. 1.350 Rp. 5.500 Rp. 1.400
Harga Periode Lalu (Pt-1) Rp. 1.000 Rp. 5.000 Rp. 1.000
Beta Saham (β) 0,8 1,2 1,5

14. • Return Realisasi
• RA = ( Rp. 1350 – Rp. 1000) / Rp. 1000 = 35 %
• RB = ( Rp. 5500 – Rp. 5000) / Rp. 5000 = 10 %
• RC = (Rp. 1400 – Rp. 1000) / Rp. 1000 = 40 %
• Retur ekspektasion yang dihitung dengan CAPM
• E(RA) = 8 % + 0,8 (20% - 8 %) = 17,6 %
• E(RB) = 8 % + 1,2 (20% - 8 %) = 22,4 %
• E(RC) = 8 % + 1,5 (20% - 8 %) = 26,0 %
• Dari hasil dapat diketahui saham A undervalued karena
return realisasinya 35 % > dari yang diharapkan 17,6 %.
Saham B overvalued karena realisasinya 10 % < dari
yang diharapkan 22,4 %. Saham C undervalued karena
return realisasinya 40 % > dari yang diharapkan 26
%.

15. Gambar 4. Letak kinerja tiga saham
Q
RB=40%
RB=35%
E(RB)=26,0 %
E(RA)=22,4 %
RM=20 %
E(RA) =17,6 %
RB =10 %
0 0,8 1,0 1,2 1,5
A
E (Ri)
RBR=8 %
𝑩𝒆𝒕𝒂
M
B
C