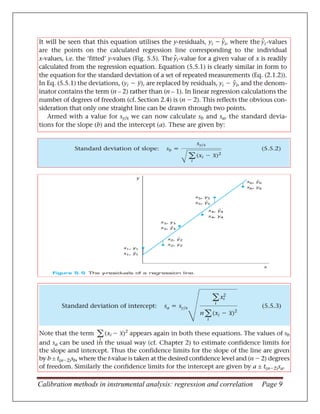
This document discusses calibration methods in instrumental analysis. It introduces instrumental analysis techniques and why they are now used for over 90% of analytical work due to advantages like sensitivity, multi-analyte capability, automation, and computer interfacing. The key steps in calibration are: (1) measuring a series of calibration standards of known concentration, (2) plotting a calibration graph of the instrument signals versus concentrations, (3) using the graph to determine unknown concentrations in test samples by interpolation. Statistical questions around the calibration graph include determining if it is linear, finding the best-fit line or curve, and calculating errors in the slope, intercept and determined concentrations.