1. The document discusses properties of inverse matrices, determinants of matrices, and their applications. Some key points include: 2. The inverse of a matrix A satisfies AA-1 = A-1A = I. The inverse of the inverse of a matrix is the original matrix. 3. For matrices AB, the inverse is B-1A-1. However, (AB)-1 is not always equal to (BA)-1. 4. The determinant of a matrix equals 0 if a whole row or column contains all 0s. The determinant is also unchanged if the rows and columns are interchanged. 5. For an inverse matrix A-1, its determinant is the reciprocal

1. SIFAT SIFAT INVERS MATRIKS
1. 𝐴𝐴−1
= 𝐴−1
A = I
Misal, 𝐴 = (
5 4
1 1
)
 𝐴−1
=
1
5−4
(
1 −4
−1 5
)
= (
1 −4
−1 5
)
 𝐴𝐴−1
= (
5 4
1 1
) (
1 −4
−1 5
)
= (
1 0
0 1
)
 𝐴−1
𝐴 = (
1 −4
−1 5
) (
5 4
1 1
)
= (
1 0
0 1
) Terbukti
2. (𝐴−1
)−1
= A
Misal, 𝐴 = (
5 4
1 1
)
 𝐴−1
=
1
5−4
(
1 −4
−1 5
)
= (
1 −4
−1 5
)
 (𝐴−1
)-1 = (
1 −4
−1 5
) -1
=
1
5−4
(
5 4
1 1
)
= (
5 4
1 1
) Terbukti
3. (𝐴𝐵)−1
= 𝐵−1
𝐴−1
Misal, A =(
5 4
1 1
) B = (
2 5
1 3
)
 𝐴−1
=
1
1
(
1 −4
−1 5
)
= (
1 −4
−1 5
)
 𝐵−1
=
1
1
(
3 −5
−1 2
)
= (
3 −5
−1 2
)

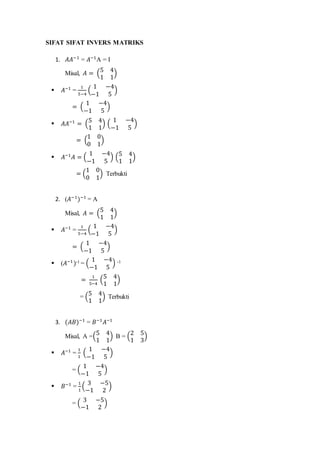
2.  (𝐴𝐵)−1
= [(
5 4
1 1
)(
2 5
1 3
)]-1
= (
14 37
3 8
)-1
=
1
1
(
8 −37
−3 14
)
= (
8 −37
−3 14
)
 𝐵−1
𝐴−1
= (
3 −5
−1 2
) (
1 −4
−1 5
)
= (
8 −37
−3 14
) Terbukti
4. (𝐴𝐵)−1
≠ (𝐵𝐴)−1
Misal, A =(
5 4
1 1
) B = (
2 5
1 3
)
 (𝐴𝐵)−1
= [(
5 4
1 1
) (
2 5
1 3
)]-1
= (
14 37
3 8
)-1
=
1
1
(
8 −37
−3 14
)
= (
8 −37
−3 14
)
 (𝐵𝐴)−1
= [(
2 5
1 3
)(
5 4
1 1
)]-1
= (
15 13
8 7
)-1
=
1
105−104
(
7 −13
−8 15
)
= (
7 −13
−8 15
) Terbukti
5. (𝐴 𝑇
)−1
= (𝐴−1
) 𝑇
Misal, A = (
2 1
2 3
)
 (𝐴 𝑇
)−1
= (
2 2
1 3
)-1
= [(
1
4
)(
3 −2
−1 2
)]

3. = (
3
4
−1
2
−1
4
1
2
)
 (𝐴−1
) 𝑇
= [(
1
4
)(
3 −2
−1 2
)]T
= (
3
4
−1
4
−1
2
1
2
) T
= (
3
4
−1
2
−1
4
1
2
) Terbukti
6. (𝐴 𝑛
)−1
= (𝐴−1
) 𝑛
Misal, A = (
1 1
1 2
)
(𝐴2
)−1
= (𝐴−1
)2
 (𝐴2
)−1
= [(
1 1
1 2
)(
1 1
1 2
)]-1
= [(
2 3
3 5
)]-1
=
1
1
(
5 −3
−3 2
)
= (
5 −3
−3 2
)
 (𝐴−1
) 𝑛
= [(
1 1
1 2
) −1
]2
= [
1
1
(
2 −1
−1 1
)]2
= (
2 −1
−1 1
)(
2 −1
−1 1
)
= (
5 −3
−3 2
) Terbukti
7. (KA)−1
=
1
𝐾
𝐴−1
Misal, A = (
1 1
1 2
)
(2A)−1
=
1
2
𝐴−1
 (2A)−1
= [2(
1 1
1 2
)]-1
= (
2 2
2 4
)-1

4. =
1
4
(
4 −2
−2 2
)
= (
1
−1
2
−1
2
1
2
)

1
2
𝐴−1
=
1
2
(
1 1
1 2
)-1
=
1
2
1
1
(
2 −1
−1 1
)
=
1
2
(
2 −1
−1 1
)
= (
1
−1
2
−1
2
1
2
) Terbukti
8. (K𝐴−1
) 𝑛
= 𝐾 𝑛
(𝐴−1
) 𝑛
Misal, A = (
1 1
1 2
)
(2𝐴−1
)2
= 22
(𝐴−1
)2
 (2𝐴−1
)2
= [2
1
1
(
2 −1
−1 1
)]2
= [(
4 −2
−2 2
)]2
= (
4 −2
−2 2
) (
4 −2
−2 2
)
= (
12 −4
−4 0
)
 22
(𝐴−1
)2
= 4 [
1
1
(
2 −1
−1 1
)]2
= 4 (
2 −1
−1 1
)(
2 −1
−1 1
)
= 4 (
3 −1
−1 0
)
= (
12 −4
−4 0
) Terbukti
9. AB = C
A = C𝐵−1
B = 𝐴−1
C
Misal, A = (
1 2
4 3
) B = (
4 3
1 2
)
C = (
6 7
19 18
)

5.  A = C𝐵−1
= (
6 7
19 18
)
1
5
(
2 −3
−1 4
)
= (
6 7
19 18
) (
2
5
−3
5
−1
5
4
5
)
= (
5
5
10
5
20
5
15
5
)
= (
1 2
4 3
) Terbukti
 B = 𝐴−1
C
=
1
−5
(
3 −2
−4 1
) (
6 7
19 18
)
= (
3
−5
2
5
4
5
1
−5
) (
6 7
19 18
)
= (
20
5
15
5
5
5
10
5
)
= (
4 3
1 2
) Terbukti
SIFAT SIFAT DETERMINAN MATRIKS
1. Apabila semua unsur dalam satu baris atau satu kolom = 0,
maka harga determinan = 0.
Misal, A = (
0 0
4 5
)
 | 𝐴| = 0 × 5 − 0 × 4
= 0-0
= 0 (Terbukti)
2. Harga determinan tidak berubah apabila semua baris diubah
menjadi kolom atau semua kolom diubah menjadi baris. Dengan kata lain
|A|=|A|T.
Misal, 𝐴 = (
2 5
1 7
) 𝐴 𝑇
= (
2 1
5 7
)

6.  | 𝐴| = 2 × 7 − 5 × 1
= 14 – 5
= 9
 | 𝐴 𝑇| = 2 × 7 − 1 × 5
= 14 – 5
= 9 (Terbukti)
3. Pertukaran tempat antara baris dengan baris atau kolom dengan kolom pada suatu
determinan akan mengubah tanda determinan.
Misal, 𝐴 = [
1 2
3 4
]
 | 𝐴| = 1 × 4 − 2 × 3
= 4 – 6
= -2
Jika baris 1 ditukar dengan baris 2 menjadi
𝐴 = [
3 4
1 2
]
 | 𝐴| = 3 × 2 − 4 × 1
= 6 – 4
= 2
Jika kolom 1 ditukar dengan kolom 2 menjadi
𝐴 = [
2 1
4 3
]
 | 𝐴| = 2 × 3 − 4 × 1
= 6 – 4
= 2 (Terbukti)
4. Apabila suatu determinan terdapat 2 baris atau 2 kolom yang identik, maka harga
determinan itu = 0
Misal, 𝐴 = [
1 2 3
1 2 3
1 −1 5
]
 | 𝐴| = (1 × 2 × 5) + (2 × 3 × 1) + (3 × 1 × (−1)) − (3 × 2 × 1) − (1 × 3 ×
(−1)) –(2 × 1 × 5)
= 10 + 6 − 3 − 6 + 3 − 10

7. = 0 (Terbukti)
5. Apabila semua unsur pada sembarang baris atau kolom dikalikan dengan
sebuah faktor (yang bukan 0), maka harga determinannya dikalikan dengan faktor
tersebut.
𝑀𝑖𝑠𝑎𝑙, 𝐴 = [
1 2
3 4
]
 | 𝐴| = 1 × 4 − 2 × 3
= 4 – 6
= -2
Misalkan baris 1 dikalikan dengan 2 maka,
A1 = [
(1 × 2) (2 × 2)
3 4
]
 | 𝐴1| = 1 × 2 × 4 − 2 × 2 × 3
= 8- 12
= -4 Terlihat bahwa | A1|=2|A|
Misalkan kolom 1 dikalikan dengan 3 maka,
A2 = [
1 × 3 2 × 3
3 4
]
 |A2| = 1 × 3 × 4 − 2 × 3 × 3
= 12-18
= -6 (Terbukti)
6. Bila A dan B bujursangkar maka |A.B|=|A|.|B|.
𝑀𝑖𝑠𝑎𝑙, 𝐴 = (
1 2
3 4
) 𝑑𝑎𝑛 𝐵 = (
1 5
2 4
)
 𝐴 × 𝐵 = (
1 × 1 + 2 × 2 1 × 5 + 2 × 4
3 × 1 + 4 × 2 3 × 5 + 4 × 4
)
= (
5 13
11 31
)
 | 𝐴 × 𝐵| = 5 × 31 − 13 × 11
= 155 − 143
= 12
 | 𝐴| × | 𝐵| = (1 × 4 − 2 × 3) × (1 × 4 − 5 × 2)
= -2 × (-6)

8. = 12 (Terbukti)
7. Jika suatu matriks merupakan matriks segitiga atas atau segitiga bawah, maka
hasil determinanya merupakan hasil kali dari elemen-elemen yang terletak pada
diagonal utamanya.
𝑀𝑖𝑠𝑎𝑙, 𝐴 = (
2 1 3
0 4 1
0 0 1
)
 | 𝐴| = 2 × 4 × 1
= 8
𝑏𝑢𝑘𝑡𝑖 = (2 × 4 × 1) + (1 × 1 × 0) + (3 × 0 × 0) − (3 × 4 × 0) − (2 × 1 × 0)
− (1 × 0 × 1)
= 8 + 0 + 0 − 0 − 0 − 0
= 8 (Terbukti)
8. | (𝐴 𝑛
)| = |A| 𝑛
Misal, A = (
1 3
0 4
)
| (𝐴2
)| = |A|2
 | (𝐴2
)| = |(
1 3
0 4
)(
1 3
0 4
)|
= |
1 15
0 16
|
= 16
 |A|2
= |
1 3
0 4
|2
= | 4 |2
= 16 (Terbukti)
9. Det 𝐴−1
=
1
det 𝐴
Misal, A = (
2 1
2 2
)
 Det 𝐴−1
= |
1
2
(
2 −1
−2 2
)|
= |
1
−1
2
−1 1
|

9. =
1
2

1
det 𝐴
=
1
4−2
=
1
2
(Terbukti )