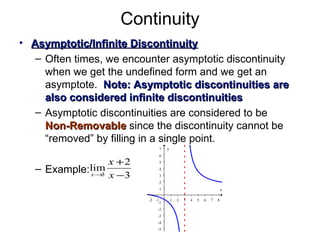
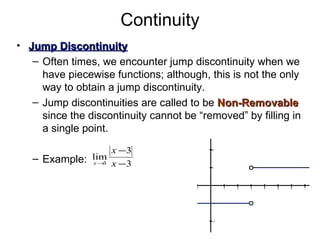
This document discusses continuity of functions. It defines a continuous function as one where the y-values approach the same limit from both sides at every point in the domain and the function is defined at every point. There are four types of discontinuities: point, asymptotic/infinite, jump, and essential. Point discontinuities can be removed by filling in a single point, while the other types are non-removable. Examples are provided to illustrate each discontinuity type. The document also examines continuity properties of polynomials, rational functions, and radical functions.

1. EDUC 553 Steve Gabel

2. Limits and Their Properties: Limits and Continuity

3. Continuity When we evaluate a limit, it’s easy as long as the function is continuous …just use Direct Substitution . But what does it mean for a function to be continuous? Our informal definition was that a function is continuous as long as you can draw the graph without lifting your pencil. This definition gives us a general idea of how continuity works but it’s not a great definition; we need a much better definition

4. Continuity Definition : A function is continuous at c if all three of the following conditions holds true: - As x gets closer and closer to c, both from the left and the right, we approach the same y-value - The function is defined at x = c - The y-value obtained from step 1 is the same as the value obtained for the function at c in step 2

5. Continuity If a function is continuous for ALL x, then we say it is a continuous function. Some functions can be continuous in certain parts of its domain and discontinuous in others There are 4 different types of discontinuity: Point discontinuity – this is where there is a “hole” in the graph or a missing point. Asymptotic/infinite discontinuity – this is when we encounter a asymptote. Jump discontinuity – this occurs when our function “jumps” from one point to another. Essential discontinuity – this happens when one side or more sides doesn’t exist or is infinite.

6. Continuity Point Discontinuity Often times, we encounter point discontinuity when we get the indeterminate form and we are able to use the cancellation technique. Point discontinuities are considered to be Removable since the discontinuity can be “removed” by filling in a single point. Example:

7. Continuity Asymptotic/Infinite Discontinuity Often times, we encounter asymptotic discontinuity when we get the undefined form and we get an asymptote. Note: Asymptotic discontinuities are also considered infinite discontinuities Asymptotic discontinuities are considered to be Non-Removable since the discontinuity cannot be “removed” by filling in a single point. Example:

8. Continuity Jump Discontinuity Often times, we encounter jump discontinuity when we have piecewise functions; although, this is not the only way to obtain a jump discontinuity. Jump discontinuities are called to be Non-Removable since the discontinuity cannot be “removed” by filling in a single point. Example:

9. Continuity Essential Discontinuity When one (or both) of our one-sided limits does not exist or goes to infinity, it is called an essential discontinuity. This can occur with radical expressions, inequalities, piece-wise functions, etc. Essential discontinuities are always Non-Removable . Note: we can consider infinite discontinuities to be essential as well. Example:

10. Continuity By examining continuity, we can make four conclusions: All polynomials are continuous All rational equations in the form of are discontinuous when g (x) = 0 All radical in the form of are continuous where a is an odd root All radical in the form of are discontinuous where a is an even root and f (x) < 0

11. Continuity - Examples Find all points of discontinuity, state the type of discontinuity, and determine if it is removable or non-removable for the following: Continuous x = -2 Continuous asymptotic disc. non-removable x = 2 point disc. removable – + + -2 < x < 3 essential disc. non-removable -2 3

12. Continuity – Piecewise Functions When dealing with piecewise functions, we must consider where the function changes. For example: jump discontinuity essential discontinuity or infinite discontinuity x = 1 non-removable x = 1 non-removable

13. Continuity – Piecewise Functions When dealing with piecewise functions, we must consider where the function changes. For example: continuous continuous asymptotic dis. x = 4 non-removable x = -4

14. Homework Continuity Read Sections TBD Problems: p. TBD