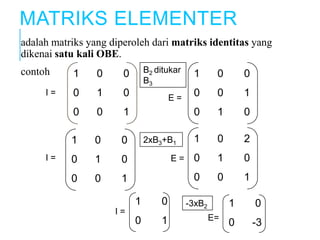
Dokumen tersebut membahas tentang matriks elementer, invers matriks, dan penggunaan invers matriks untuk menyelesaikan sistem persamaan linear (SPL). Secara singkat, matriks elementer adalah hasil dari satu kali operasi baris elemen matriks, sedangkan invers matriks digunakan untuk menyelesaikan SPL dengan mengubahnya menjadi perkalian matriks.

1. MATRIKS
ELEMENTER &
INVERS

2. MATRIKS ELEMENTER
adalah matriks yang diperoleh dari matriks identitas yang
dikenai satu kali OBE.
contoh 1 0 0
0 1 0
0 0 1
I =
1 0 0
0 0 1
0 1 0
B2 ditukar
B3
1 0 0
0 1 0
0 0 1
I =
1 0 2
0 1 0
0 0 1
2xB3+B1
1 0
0 1
I =
1 0
0 -3
-3xB2
E =
E =
E=

3. INVERS MATRIKS (2 X 2)
Jika A =
maka invers matriks A
ad – bc = determinan matriks A atau det.A (IAI)
Jika ad – bc = 0  matriks tidak mempunyai
invers (matriks singular)
dc
ba
ac
bd11
bc-ad
A

4. CONTOH
invers matriks A = adalah….
35
12
25
13
5-6
1
25
13
1.5-2.3
1
A
1
25
13
ac
bd
bc-ad
1
A
1

5. TEOREMA INVERS MATRIK
(A-1)
Jika A dan B adalah matriks-matriks yang dapat dibalik dan
yang ukurannya sama, maka
 A B = B A = I  A adalah invers dari B dan B adalah invers dari A
 Jika B = invers A (di tulis A-1) maka A. A-1 = A-1. A = I
 (AB)-1 = B-1A-1
A-n = (A-1) n = A-1A-1…A-1 , untuk n = 0, 1, 2, …
A-1 dapat dibalik dan (A-1)-1 = A
(kA)-1 = 1/k A-1 , untuk setiap skalar k ≠ 0 (Coba buktikan!
poin plus)
•Tiap-tiap matriks elementer dapat dibalik dan inversnya
adalah juga sebuah matriks elementer (Coba buktikan!
poin plus)

6. 52
31
A = dan B =
12
35
A x B =
52
31
12
35
=
-5+6 -3+3
10-10 6-5
=
10
01
= I
CONTOH A B = B A = I
B x A =
52
31
12
35
= -5+6 -15+15
2-2 6-5
=
10
01
= I
B = invers A (di tulis A-1) maka
A. A-1 = A-1. A = I

7. CONTOH (AB)-1 = B-1A-1
3 2
2 2
1 2
1 3
A = B = A B =
1 -1
-1 3/2
7 6
9 8
4 -3
-9/2 7/2
(AB)-1=
B-1A-1 = =
3 -2
-1 1
A-1 = B-1 =
1 -1
-1 3/2
3 -2
-1 1
4 -3
-9/2 7/2
11
23
1.23.1
1
32
22
2.22.3
1
= =
79
68
9.68.7
1

8. CONTOH (A-1)-1 = A
24
131
A
4.12.3
1
)(A
11
2
3
-1
-4
34
12
2
1
2
3
2
1
2
1
AmatriksJadi
2
3
2
1
2
1
A Buktikan (A-1)-1 = A

9. INVERS (MENGGUNAKAN OBE)
(CONT.)
OBE yang mengubah I
menjadi E
Operasi invers
(OBE yang mengubah E
menjadi I)
Kalikan baris ke i dengan c ≠ 0 Kalikan baris ke i dengan 1/c
Pertukarkan baris ke i dengan
baris ke j
Pertukarkan baris ke j
dengan baris ke i
Tambahkan c kali baris ke i ke
baris ke j
Tambahkan –c kali baris ke i
ke baris ke j
1
)( AI
OBE
IA
atau

10. INVERS OBE (CONTOH-1)
801
352
321
A
Carilah A-1 dengan OBE
100
010
001
801
352
321
IA
(-2)B1+B2
(-1)B1+B3
101
012
001
520
310
321
(-2)B2+B3
2B2+B1
125
012
025
100
310
901

11. (-9) B3+B1
3 B3+B2
125
3513
91640
100
010
001
125
3513
91640
1
AJadi,
(-1) B3
125
012
025
100
310
901
INVERS OBE (CONTOH-1)

12. INVERS OBE (CONTOH-2)
13
21
A Carilah A-1 dengan OBE
10
01
13
21
IA
10
01
13
21(-1) B1
13
01
70
21(-3) B1 + B2
7/17/3
01
10
21(1/7) B2
7/17/3
7/27/1
10
012 B2 + B1
7/17/3
7/27/11
AJadi,

13. PENYELESAIAN SPL DENGAN INVERS
MATRIKS
Tentukan nilai x dan y dari SPL berikut
2x + y = 5
4x – 5y = 3
3
5
54
12
y
x
A X B
• Jika SPL  A X = B
• Maka X = A-1 B
Contoh
Buat matriksnya

14. PENYELESAIAN SPL DENGAN INVERS
MATRIKS
10
01
54
12
10
02/1
54
2/11(½)B1
12
02/1
70
2/11(-4)B1+B2
7/17/2
02/1
10
2/11(-1/7) B2
7/17/2
14/114/5
10
01(-1/2)B2+B1
Cari nilai x dan y dengan cara
biasa (poin plus)
)3)(7/1()5)(7/2(
)3)(14/1()5)(14/5(
3
5
7/17/2
14/114/5
X
X = A-1 B
Y
X
1
2
7/7
14/28

15. PENYELESAIAN SPL DENGAN
INVERS MATRIKS
Jika A = dan B =
Tentukan matriks A (2x2) yang memenuhi:
a. A X = B
b. X A = B
12
35
05
12
52
31
3.2-5.1
1
A
1
52
31
52
31
1-
1
Contoh
Cari A-1 terlebih dulu

16. a.Jika A X = B
maka X = A-1.B
05
12
52
31
X .
02)25(4
01512
229
117
XJadi
b. Jika X A = B
maka X = B.A-1
52
3
05
12
X
1-
.
155
114
XJadi
0150)5(
5)()6(22
PENYELESAIAN SPL DENGAN
INVERS MATRIKS

17. TUGAS (KUMPULKAN
PERTEMUAN BERIKUTNYA)
Carilah invers (A-1) dari A =
dengan dua cara
Tentukan nilai dari X1, X2, dan X3 dengan menggunakan OBE
X1 + X2 – X3 = -3
2X1 + X2 + X3 = 4
X1 + 2X2 + X3 = 7
34
12