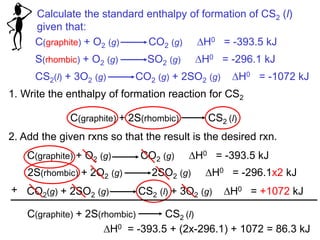
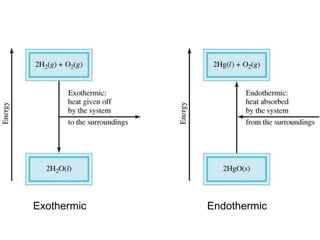
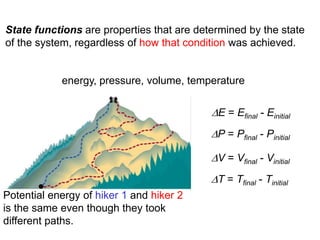
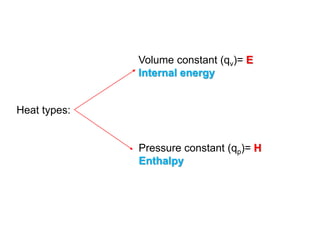
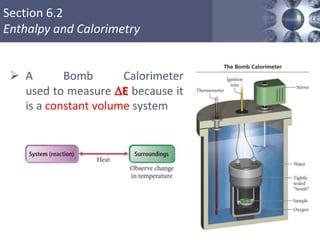
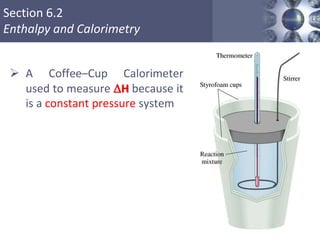
Thermochemistry is the study of heat changes in chemical reactions. Thermal energy is the energy associated with the random motion of atoms and molecules. Enthalpy (H) is a state function that represents the total energy of a system at constant pressure. The standard enthalpy of formation (ΔHf°) is the change in enthalpy that accompanies the formation of one mole of a compound from its elements in their standard states. Hess's law states that the enthalpy change for a reaction is equal to the sum of the enthalpy changes of the steps in any possible pathway between the initial and final states of the reaction.

2. Chapter 6
Thermochemistry

3. Thermochemistry

4. Section 6.1
The Nature of Energy
Thermochemistry is the study of heat change in chemical
reactions.

5. Energy

6. Section 6.1
The Nature of Energy
Copyright © Cengage Learning. All rights reserved 6
 Capacity to do work or to produce heat.
 Law of conservation of energy – energy can
be converted from one form to another but
can be neither created nor destroyed.
Energy

7. Energy Types

8. Section 6.1
The Nature of Energy
8
 Energy
 Potential energy – is energy that is stored in an object
or energy due to position or composition.
 Kinetic energy – is energy of motion of the object and
depends on the mass of the object and its velocity.
Potential energy
Kinetic energy
thermal energy
is kinetic

9. Some Forms of Energy
• Electrical
 kinetic energy associated with the flow of electrical charge
• Heat or Thermal Energy
 kinetic energy associated with molecular motion
• Light or Radiant Energy
 kinetic energy associated with energy transitions in an atom
• Nuclear
 potential energy in the nucleus of atoms
• Chemical
 potential energy in the attachment of atoms or because of
their position

10. Units of Energy
• Joule (J) is the amount of energy needed to move
a 1 kg mass a distance of 1 meter
1 J = 1 N∙m = 1 kg∙m2/s2
• calorie (cal) is the amount of energy needed to
raise one gram of water by 1°C
kcal = energy needed to raise 1000 g of water 1°C
food Calories = kcals
Energy Conversion Factors
1 calorie (cal) = 4.184 joules (J) (exact)

11. Thermal energy

12. Section 6.1
The Nature of Energy
Thermal energy is the energy associated with the random
motion of atoms and molecules

13. Heat is the transfer of thermal energy between two bodies that
are at different temperatures.
Energy Changes in Chemical Reactions
Temperature is a measure of the thermal energy.
900C
400C
greater thermal energy
Temperature = Thermal Energy

14. System and Surroundings

15. Section 6.1
The Nature of Energy
Copyright © Cengage Learning. All rights reserved 15
 The system is the specific part of the universe that
is of interest in the study.
 Surroundings – include everything else in the
universe.
open
mass & energyExchange:
closed
energy
isolated
nothing

16. Exothermic & Endothermic process

17. Exothermic process is any process that gives off heat –
transfers thermal energy from the system to the surroundings.
Endothermic process is any process in which heat has to be
supplied to the system from the surroundings.
2H2 (g) + O2 (g) 2H2O (l) + energy
H2O (g) H2O (l) + energy
energy + 2HgO (s) 2Hg (l) + O2 (g)
energy + H2O (s) H2O (l)

18. Exothermic Endothermic

19. Section 6.1
The Nature of Energy
Copyright © Cengage Learning. All rights reserved 19
Is the freezing of water an endothermic or exothermic
process? Explain.
CONCEPT CHECK!
Exothermic process because you must remove energy
in order to slow the molecules down to form a
solid.

20. Section 6.1
The Nature of Energy
Copyright © Cengage Learning. All rights reserved 20
Classify each process as exothermic or
endothermic. Explain. The system is underlined in
each example.
a) Your hand gets cold when you touch
ice.
b) The ice gets warmer when you touch it.
c) Water boils in a kettle being heated on a
stove.
d) Water vapor condenses on a cold pipe.
e) Ice cream melts.
Exo
Endo
Endo
Exo
Endo
CONCEPT CHECK!

21. State functions

22. State functions are properties that are determined by the state
of the system, regardless of how that condition was achieved.
Potential energy of hiker 1 and hiker 2
is the same even though they took
different paths.
energy, pressure, volume, temperature
DE = Efinal - Einitial
DP = Pfinal - Pinitial
DV = Vfinal - Vinitial
DT = Tfinal - Tinitial

23. Path functions

24. Work is not a state function. Why?
w = F x d
F= Force
d= distance
Dw = wfinal - winitial
P x V = x d3 = F x d = w
F
d2
w = -P DV
different distances different works
Therefore work is path function not state function

25. Enthalpy and Calorimetry

26. Section 6.2
Enthalpy and Calorimetry
 Calorimetry: Science of measuring heat
 Specific heat capacity (s):
The amount of heat (q) required to raise the
temperature of one gram of a substance by one degree
Celsius.
 Molar heat capacity (C):
 The amount of heat (q) required to raise the
temperature of one mole of substance by one degree
Celsius.
Copyright © Cengage Learning. All rights reserved 26
C = m x s

27. Section 6.2
Enthalpy and Calorimetry
Heat = (mass) x (specific heat capacity) x (temp. change)
q = m.s.DT
 q= Heat (J)
 s = specific heat capacity (J/°C·g)
 m = mass of solution (g)
 ΔT = change in temperature (°C)
27

28. How much heat is given off when an 869 g iron bar cools
from 940C to 50C? s of Fe = 0.444 J/g • 0C
Dt = tfinal – tinitial = 50C – 940C = -89 0C
q = msDt = 869 g x 0.444 J/g • 0C x –890C = -34,000 J

29. How much heat is absorbed by a copper penny with mass
3.1 g whose temperature rises from -8 0C to 37 0C?
s of Cu = 0.385 J/g. 0C
Dt = tfinal – tinitial = 37 0C – (-8 0C) = 45 0C
q = msDt = 3.1 g x 0.385 J/g • 0C x 45 0C = 53.7 J

30. Heat types:
Volume constant (qv)= E
Internal energy
Pressure constant (qp)= H
Enthalpy

31. Calorimeter

32. Section 6.2
Enthalpy and Calorimetry
 A Bomb Calorimeter
used to measure DE because it
is a constant volume system
Copyright © Cengage Learning. All rights reserved 32

33. Section 6.2
Enthalpy and Calorimetry
 A Coffee–Cup Calorimeter
used to measure DH because it
is a constant pressure system
Copyright © Cengage Learning. All rights reserved 33

34. Section 6.2
Enthalpy and Calorimetry
Change in Enthalpy
 Entalpy is the state function
ΔH = Hproducts – Hreactants
Copyright © Cengage Learning. All rights reserved 34
 When reaction is multiplied by a factor, ΔH is multiplied by that
factor
C(s) + O2(g) → CO2(g) ΔH = -393.5 kJ
2 C(s) + 2 O2(g) → 2 CO2(g) ΔH = 2(-393.5 kJ) = 787.0 kJ
If a reaction is reversed, then the sign of ΔH is reversed
CO2(g) → C(s) + O2(g) ΔH = +393.5 kJ

35. Calculate ΔH in which 13.2 kg of propane is burned in
excess oxygen at constant pressure.
C3H8(g) + 5O2(g) → 3CO2(g) + 4H2O(l) ΔH = –2044 kJ
kJ1012.6
mol1
kJ2044-
g44.09
mol1
1kg
g1000
kg13.2 5


36. Hess's Law

37. • if a reaction can be expressed as a series of steps, then
the ΔH for the overall reaction is the sum of the ΔHs of
reaction for each step.
1) A + 2B C ΔH1
2) C 2D ΔH2
A + 2B 2D ΔH3= ΔH1+ΔH2

38. Section 6.3
Hess’s Law
 This reaction also can be carried out in two distinct steps,
with enthalpy changes designated by ΔH2 and ΔH3.
N2(g) + O2(g) → 2NO(g) ΔH2 = 180 kJ
2NO(g) + O2(g) → 2NO2(g) ΔH3 = – 112 kJ
N2(g) + 2O2(g) → 2NO2(g) ΔH2 + ΔH3 = 68 kJ
ΔH1 = ΔH2 + ΔH3 = 68 kJ
N2(g) + 2O2(g) → 2NO2(g) ΔH1 = 68 kJ
Copyright © Cengage Learning. All rights reserved 38

39. Section 6.3
Hess’s Law
Example
 Consider the following data:
 Calculate ΔH for the reaction
Copyright © Cengage Learning. All rights reserved 39
3 2 2
2 2 2
1 3
2 2
NH ( ) N ( ) H ( ) H = 46 kJ
2 H ( ) O ( ) 2 H O( ) H = 484 kJ
  D
  D 
g g g
g g g
2 2 2 32 N ( ) 6 H O( ) 3 O ( ) 4 NH ( )  g g g g

40. Section 6.3
Hess’s Law
Example
 Reverse the two reactions:
 Desired reaction:
Copyright © Cengage Learning. All rights reserved 40
2 2 2 32 N ( ) 6 H O( ) 3 O ( ) 4 NH ( )  g g g g
2 2 3
2 2 2
1 3
2 2
N ( ) H ( ) NH ( ) H = 46 kJ
2 H O( ) 2 H ( ) O ( ) H = +484 kJ
  D 
  D
g g g
g g g

41. Section 6.3
Hess’s Law
Example
 Multiply reactions to give the correct numbers of
reactants and products:
4( ) 4( )
3( ) 3( )
 Desired reaction:
2 2 2 32 N ( ) 6 H O( ) 3 O ( ) 4 NH ( )  g g g g
2 2 3
2 2 2
1 3
2 2
N ( ) H ( ) NH ( ) H = 46 kJ
2 H O( ) 2 H ( ) O ( ) H = +484 kJ
  D 
  D
g g g
g g g

42. Section 6.3
Hess’s Law
Example
 Final reactions:
 Desired reaction:
ΔH = +1268 kJ
Copyright © Cengage Learning. All rights reserved 42
2 2 2 32 N ( ) 6 H O( ) 3 O ( ) 4 NH ( )  g g g g
2 2 3
2 2 2
2 N ( ) 6 H ( ) 4 NH ( ) H = 184 kJ
6 H O( ) 6 H ( ) 3 O ( ) H = +1452 kJ
  D 
  D
g g g
g g g

43. Standard Enthalpy of Formation (ΔHf°)

44. Section 6.4
Standard Enthalpies of Formation
 Change in enthalpy that accompanies the formation of
one mole of a compound from its elements with all
substances in their standard states.
44
aA + bB cC + dD
DH0 dDH0 (D)
f
cDH0 (C)
f= [ + ] - bDH0 (B)
f
aDH0 (A)
f
[ + ]
DH0
nDH0 (products)
f= S mDH0 (reactants)
f
S-

46. Section 6.4
Standard Enthalpies of Formation
Conventional Definitions of Standard States
 For a Compound
 For a gas, pressure is exactly 1 atm.
 For a solution, concentration is exactly 1 M.
 For an Element
Copyright © Cengage Learning. All rights reserved 46
The standard enthalpy of formation of any element in its
most stable form is zero.
DH0 (O2) = 0f
DH0 (O3) = 142 kJ/molf
DH0 (C, graphite) = 0f
DH0 (C, diamond) = 1.90 kJ/molf
DH0 (C, monoclinic) = 1.90 kJ/molDH0 (S, rhombic) = 0f

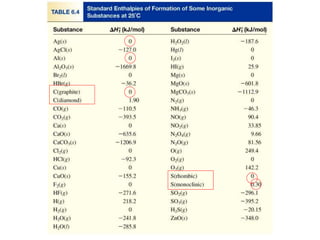
47. Benzene (C6H6) burns in air to produce carbon dioxide and
liquid water. How much heat is released per mole of
benzene combusted? The standard enthalpy of formation
of benzene is 49.04 kJ/mol.
2C6H6 (l) + 15O2 (g) 12CO2 (g) + 6H2O (l)
DH0
rxn nDH0 (products)f= S mDH0 (reactants)fS-
DH0
rxn 6DH0 (H2O)f12DH0 (CO2)f= [ + ] - 2DH0 (C6H6)f[ ]
DH0
rxn = [ 12x–393.5 + 6x–187.6 ] – [ 2x49.04 ] = -5946 kJ
-5946 kJ
2 mol
= - 2973 kJ/mol C6H6
6.6

48. Calculate the standard enthalpy of formation of CS2 (l)
given that:
C(graphite) + O2 (g) CO2 (g) DH0 = -393.5 kJ
S(rhombic) + O2 (g) SO2 (g) DH0 = -296.1 kJ
CS2(l) + 3O2 (g) CO2 (g) + 2SO2 (g) DH0 = -1072 kJ
1. Write the enthalpy of formation reaction for CS2
C(graphite) + 2S(rhombic) CS2 (l)
2. Add the given rxns so that the result is the desired rxn.
C(graphite) + O2 (g) CO2 (g) DH0 = -393.5 kJ
2S(rhombic) + 2O2 (g) 2SO2 (g) DH0 = -296.1x2 kJ
CO2(g) + 2SO2 (g) CS2 (l) + 3O2 (g) DH0 = +1072 kJ+
C(graphite) + 2S(rhombic) CS2 (l)
DH0 = -393.5 + (2x-296.1) + 1072 = 86.3 kJ

49. The end