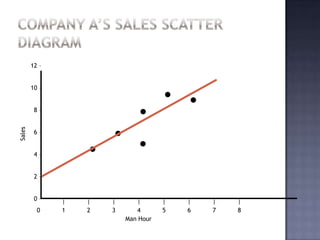
This document discusses linear regression analysis. It defines linear regression and its key assumptions. Regression is used to estimate the relationship between a dependent and independent variable. The document provides an example of a company using regression to analyze the relationship between sales and man-hours. Calculations are shown to estimate the regression line and measure how much of the variation in sales is explained by variation in man-hours. Key outputs like the coefficient of determination and correlation coefficient are also introduced.

1. Quantitative Analysis for BusinessLecture 2July 5th, 2010Saksarun (Jay) Mativachranon

2. IntroPlease turn your mobile phones off or switch it to silent modeand please do not pick up your callsSlide will be available atwww.slideshow.com (soon)Email: saarkman@gmail.com

3. Linear regression

4. RegressionRegression is used for estimating the unknown effect of changing one variable over anotherThe variable to be estimated is called “dependent variable”The changing variable is called “independent variable”

5. Linear Regression AssumptionsThere is NO relationship between X and Y if 1 equals to 0There is ALWAYS a relationship if 1 does NOT equal to 0The independent Variable (X) is not randomThe expected value of error (e ) is 0

6. Linear Regression AnalysisAnalyzing the correlation and directionality of the dataEstimating the modelEvaluating the validity and usefulness of the model

7. Usage of RegressionCausal analysisForecasting an effect (of independent variable to that of dependent variable)Forecasting (trend of) future values

8. Simple Linear RegressionTrue value of slope and intercept are not known, so we estimate them by using sample datawhere Y = dependent variable X = independent variable b0 = intercept (value of Y when X = 0) b1 = slope of the regression line^

9. Scatter Diagram

10. exampleLinear Regression

11. SituationCompany A wants to know the relationship between the Man Hour of their sales force and their sales numberThey have collected their sales data and the man hour put in during the collection period

12. Company A Data

13. Company A’s Sales Scatter Diagram12 –10 –8 –6 –4 –2 –0 –Sales | | | | | | | | 0 1 2 3 4 5 6 7 8Man Hour

14. Finding the RegressionCompany A is trying to predict its sales from the man hour spentThe line in is the one that minimizes the errorsY = SalesX = Man HourError = (Actual value) – (Predicted value)

15. Data manipulationFor the simple linear regression model, the values of the intercept and slope can be calculated using the formulas below

16. Regression Calculation________

17. Regression Calculation (cont.)Therefore

18. ResultsCompany A Sales modelPredicting salesEvery 1 Man-hour, Company A sells $3.25 worth of goods

19. Measuring Regression ModelRegression model can be developed for any variable Y and XBut how do we know the reliability of Y from variation of X ???

20. Company A’s Sales Model12 –10 –8 –6 –4 –2 –0 –Sales | | | | | | | | 0 1 2 3 4 5 6 7 8Man HourErrorError

21. Measuring Regression Model (cont.)How do we know the reliability of Y from variation of X ???Can we find the average of the errors?

22. Measurement of VariabilitySST – Total variability about the meanSSE – Variability about the regression lineSSR – Total variability that is explained by the model

23. Measurement of VariabilitySum of the squares totalSum of the squared errorSum of squares due to regressionAn important relationship

24. Company A example__^^^__^^_

25. Company A’s VariabilitySST = 22.5SSE = 6.875SSR = 15.625

26. Company A’s Sales Model12 –10 –8 –6 –4 –2 –0 –^Y = 2 + 1.25X^Y – YYSalesY – YY – Y^ | | | | | | | | 0 1 2 3 4 5 6 7 8Man Hour

27. Coefficient of DeterminationThe proportion of variability of Y in the regression model

28. Coefficient of DeterminationThe coefficient of determination is r2

29. Company A exampleExplanationOver 69% of Y can be predicted by variation of XFor Company A

30. Correlation CoefficientThe strength of linear relationshipRelationship of Y and XIt will always be between +1 and –1The correlation coefficient is r

31. Correlation CoefficientYY****************XX(a) Perfect PositiveCorrelation: r = +1(b) PositiveCorrelation: 0 < r < 1YY******************XX(c) No Correlation: r = 0(d) Perfect Negative Correlation: r = –1

32. Next WeekLinear RegressionErrors in Regression modelVarianceMean Square ErrorStandard DeviationTesting the ModelMultiple Regression