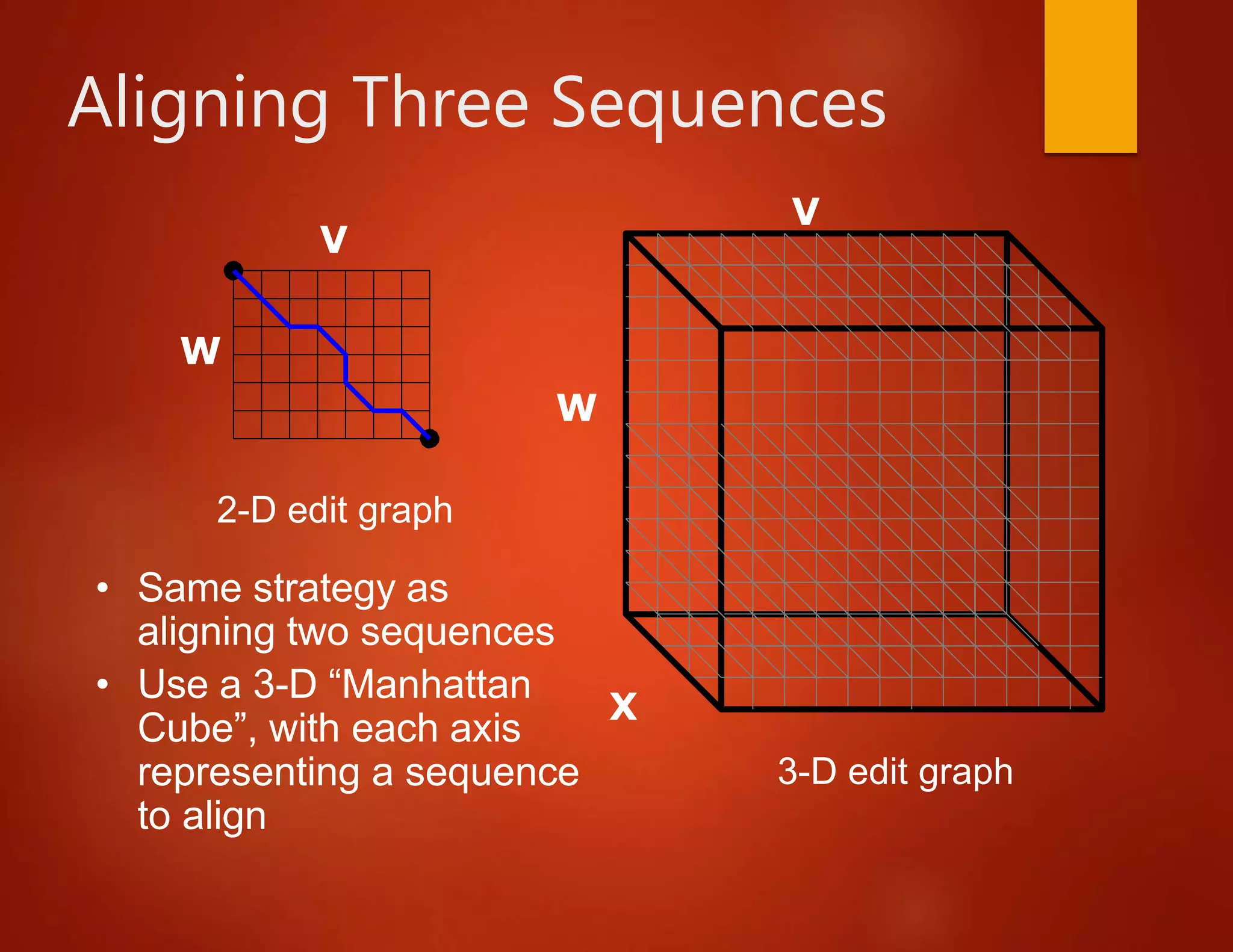
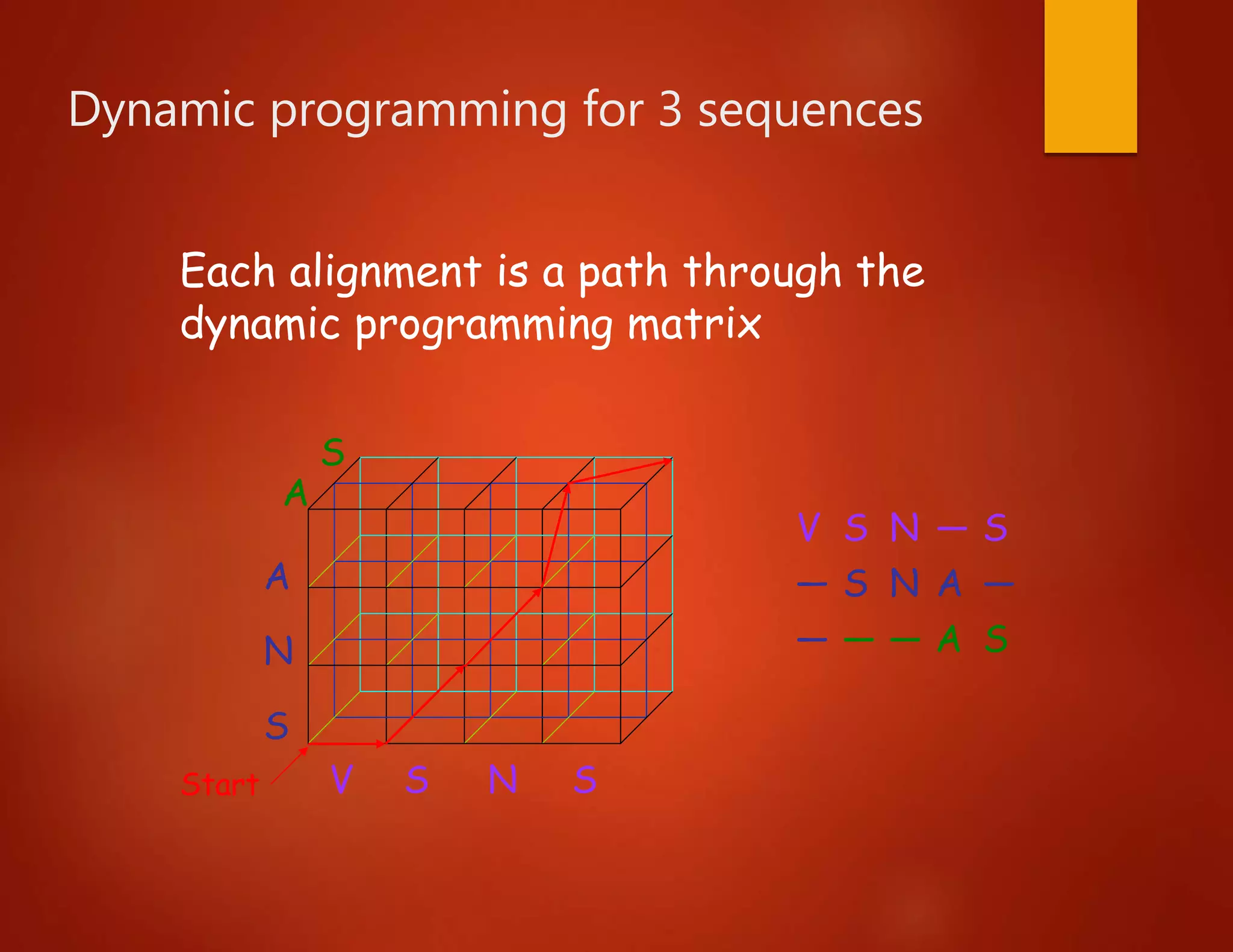
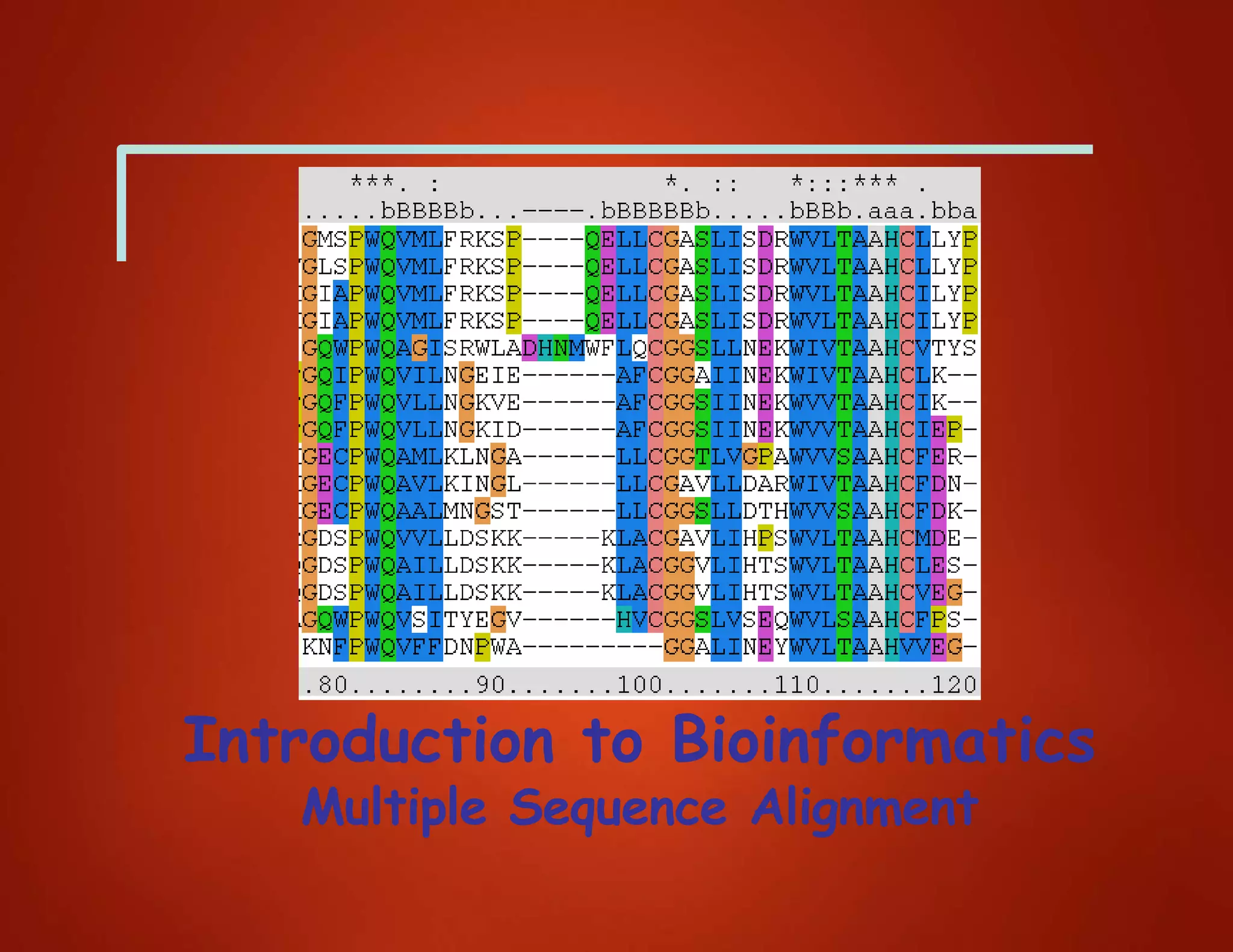
This document discusses multiple sequence alignment (MSA), which involves aligning more than two biological sequences, such as DNA, RNA, or protein sequences. MSA can reveal subtle similarities between sequences that pairwise alignment cannot by identifying conserved regions present in many sequences. The document describes different approaches to MSA, including optimal global alignments using dynamic programming, progressive alignments, and iterative alignments. It notes challenges like computational expense and difficulty of scoring and identifying ancestry relationships with more divergent sequences. The dynamic programming approach to aligning three sequences using a 3D "Manhattan cube" representation is also explained.

1. Introduction to Bioinformatics
Multiple Sequence Alignment

2. Why Multiple Sequence Alignment?
• Up until now we have only
tried to align two sequences.
• What about more than two?
And what for?
• A faint similarity between two
sequences becomes significant
if present in many
• Multiple alignments can
reveal subtle similarities that
pairwise alignments do not
reveal
V T I S C T G S S S N I G
V T LT C T G S S S N I G
V T LS C S S S G F I F S
V T LT C T V S G T S F D
V T I T C V V S D V S H E
V T LV C L I S D F Y P G
V T LV C L I S D F Y P G
V T LV C L VS D Y F P E

3. Multiple Sequence Alignment
(msa) VTISCTGSSSNIGAGNHVKWYQQLPG
VTISCTGTSSNIGSITVNWYQQLPG
LRLSCSSSGFIFSSYAMYWVRQAPG
LSLTCTVSGTSFDDYYSTWVRQPPG
PEVTCVVVDVSHEDPQVKFNWYVDG
ATLVCLISDFYPGAVTVAWKADS
ATLVCLISDFYPGAVTVAWKADS
AALGCLVKDYFPEPVTVSWNSG-
VSLTCLVKGFYPSDIAVEWESNG-
• Goal: Bring the greatest number of similar
characters into the same column of the alignment
• Similar to alignment of two sequences.

4. Multiple Sequence Alignment: Motivation
• Correspondence. Find out which parts “do the same thing”
– Similar genes are conserved across widely divergent species,
often performing similar functions
• Structure prediction
– Use knowledge of structure of one or more members of a
protein MSA to predict structure of other members
– Structure is more conserved than sequence
• Create “profiles” for protein families
– Allow us to search for other members of the family
• Genome assembly: Automated reconstruction of “contig”
maps of genomic fragments such as ESTs
• msa is the starting point for phylogenetic analysis
• msa often allows to detect weakly conserved regions which
pairwise alignment can’t

5. Multiple Sequence Alignment: Approaches
• Optimal Global Alignments -
– Generalization of Dynamic programming
– Find alignment that maximizes a score function
– Computationally expensive: Time grows as product
of sequence lengths
• Global Progressive Alignments - Match closely-
related sequences first using a guide tree
• Global Iterative Alignments - Multiple re-building
attempts to find best alignment
• Local alignments
– Profile analysis,
– Block analysis
– Patterns searching and/or Statistical methods

6. Global msa: Challenges
• Computationally Expensive
– If msa includes matches, mismatches and gaps and also
accounts the degree of variation then global msa can be
applied to only a few sequences
• Difficult to score
– Multiple comparison necessary in each column of the msa for
a cumulative score
– Placement of gaps and scoring of substitution is more difficult
• Difficulty increases with diversity
– Relatively easy for a set of closely related sequences
– Identifying the correct ancestry relationships for a set of
distantly related sequences is more challenging
– Even difficult if some members are more alike compared
to others

7. Global msa: Dynamic
Programming
• The two-sequence alignment algorithm (Needleman-
Wunsch) can be generalized to any number of
sequences.
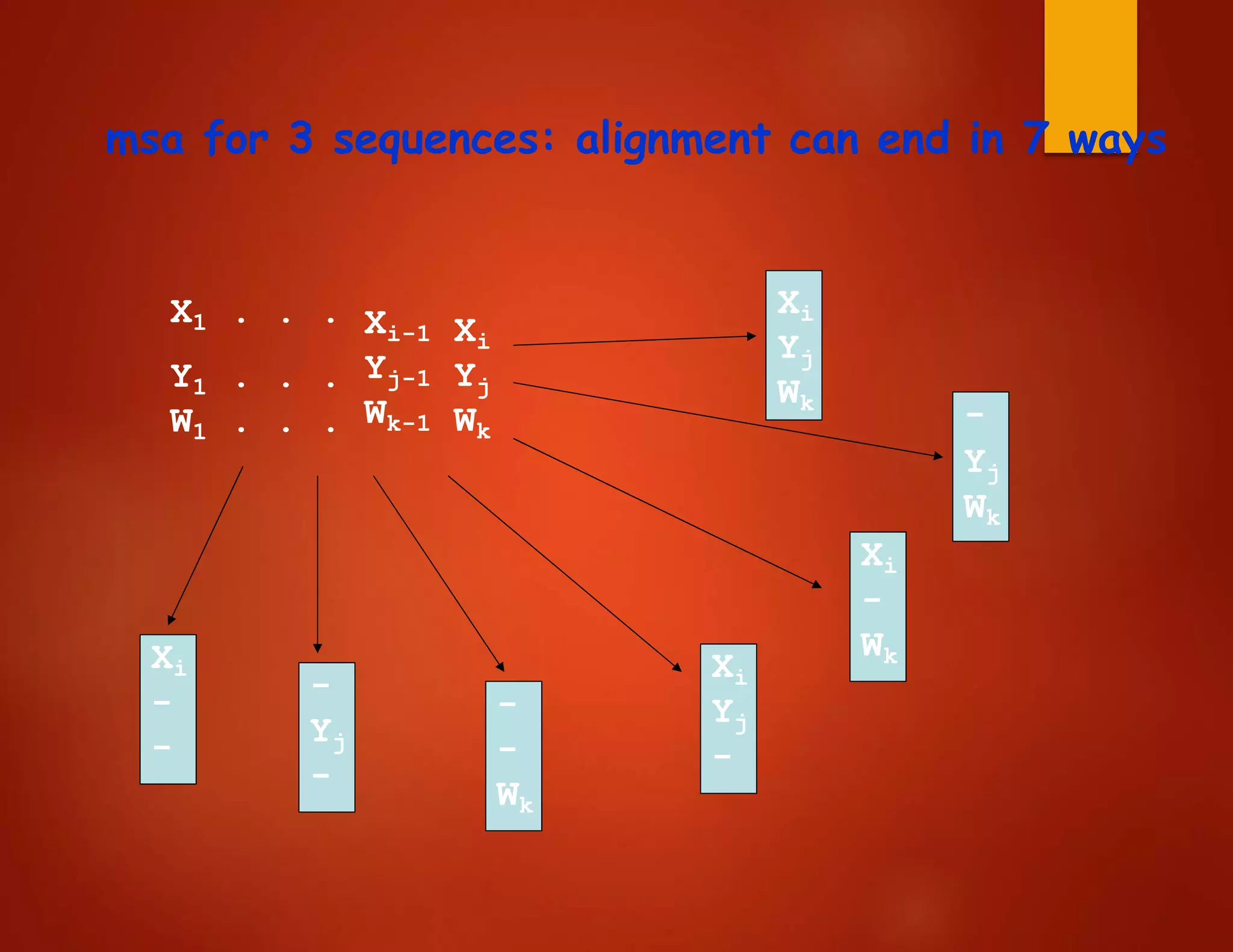
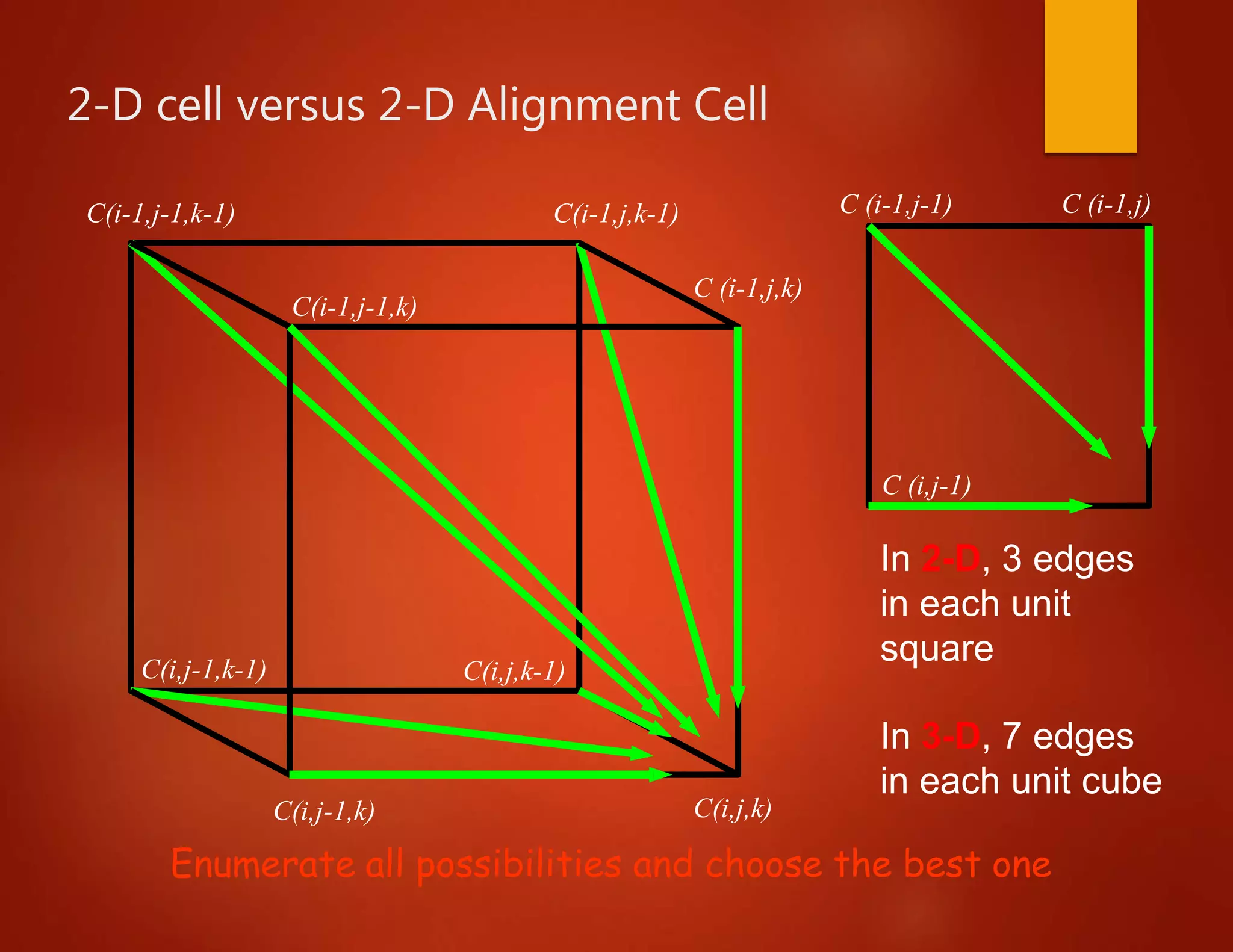
• E.g., for three sequences X, Y, W
define C[i,j,k] = score of optimum
alignment
 among X[1..i], Y[1..j], W[1..k]
• As for two sequences, divide possible alignments into
different classes, depending on how they end.
– Devise recurrence relations for C[i,j,k]
– C[i,j,k] is the maximum out of all possibilities

8. Xi
Yj
Wk
msa for 3 sequences: alignment can end in 7 ways
Xi-1
Yj-1
Wk-1
Xi
Yj
Wk
-
Yj
Wk
Xi
-
Wk
Xi
Yj
-
-
-
Wk
-
Yj
-
Xi
-
-
X1 . . .
Y1 . . .
W1 . . .

9. Aligning Three Sequences
• Same strategy as
aligning two sequences
• Use a 3-D “Manhattan
Cube”, with each axis
representing a sequence
to align
V
W
2-D edit graph
3-D edit graph
V
W
X

10. Dynamic programming for 3 sequences
V S N — S
— S N A —
— — — A S
V S N S
A
N
S
Each alignment is a path through the
dynamic programming matrix
S
A
Start

11. 2-D cell versus 2-D Alignment Cell
In 3-D, 7 edges
in each unit cube
In 2-D, 3 edges
in each unit
square
C(i-1,j-1,k-1) C(i-1,j,k-1)
C(i,j-1,k)
C(i-1,j-1,k)
C (i-1,j,k)
C(i,j,k)
C(i,j,k-1)C(i,j-1,k-1)
Enumerate all possibilities and choose the best one
C (i-1,j-1) C (i-1,j)
C (i,j-1)

12. Multiple Alignment: Dynamic Programming
• si,j,k = max
• (x, y, z) is an entry in the 3-D scoring matrix
si-1,j-1,k-1 + (vi, wj, uk)
si-1,j-1,k +  (vi, wj, _ )
si-1,j,k-1 +  (v , _, u )i k
si,j-1,k-1
si-1,j,k
si,j-1,k
si,j,k-1
+  (_, wj, uk)
+  (vi, _ , _)
+  (_, wj, _)
+  (_, _, uk)
cube diagonal:
no in/dels
face diagonal:
one in/del
edge diagonal:
two in/dels

13. • Reading Materials
– Chapter 5: Bioinformatics Sequence and Genome
analysis – David W. Mount
• 2nd Edition: Page 170~194
• 1st Edition: Page 140~165
– Cédric Notredame, Desmond G. Higgins and Jaap Heringa “T-
coffee: a novel method for fast and accurate multiple
sequence alignment”, Journal of Molecular Biology, Volume
302, Issue 1, 8 September 2000, Pages 205-217
– Christopher Lee, Catherine Grasso and Mark F. Sharlow,
“Multiple sequence alignment using partial order graphs”
Bioinformatics Vol. 18 no. 3 2002, Pages 452-464
– Cédric Notredame and Desmond G. Higgins “SAGA: sequence
alignment by genetic algorithm”, Nucleic Acids Res. 1996 Apr
15;24(8):1515-24.